Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-20T17:18:04.729Z Has data issue: false hasContentIssue false
  • English
  • Français

Convectively driven shear and decreased heat flux

Published online by Cambridge University Press:  31 October 2014

David Goluskin ,
Hans Johnston ,
Glenn R. Flierl  and
Edward A. Spiegel
David Goluskin*
Affiliation:
Department of Applied Physics and Applied Mathematics, Columbia University, New York, NY 10027, USA
Hans Johnston
Affiliation:
Department of Mathematics and Statistics, University of Massachusetts, Amherst, MA 01003, USA
Glenn R. Flierl
Affiliation:
Department of Earth, Atmospheric, and Planetary Sciences, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
Edward A. Spiegel
Affiliation:
Department of Astronomy, Columbia University, New York, NY 10027, USA New York University, New York, NY, USA
*
†Present address: Mathematics Department, University of Michigan, Ann Arbor, MI 48109, USA. Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We report on direct numerical simulations of two-dimensional, horizontally periodic Rayleigh–Bénard convection between free-slip boundaries. We focus on the ability of the convection to drive large-scale horizontal flow that is vertically sheared. For the Prandtl numbers (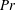$\mathit{Pr}$) between 1 and 10 simulated here, this large-scale shear can be induced by raising the Rayleigh number (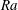$\mathit{Ra}$) sufficiently, and we explore the resulting convection for 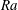$\mathit{Ra}$ up to 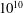$10^{10}$. When present in our simulations, the sheared mean flow accounts for a large fraction of the total kinetic energy, and this fraction tends towards unity as 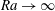$\mathit{Ra}\rightarrow \infty$. The shear helps disperse convective structures, and it reduces vertical heat flux; in parameter regimes where one state with large-scale shear and one without are both stable, the Nusselt number of the state with shear is smaller and grows more slowly with 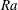$\mathit{Ra}$. When the large-scale shear is present with 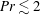$\mathit{Pr}\lesssim 2$, the convection undergoes strong global oscillations on long timescales, and heat transport occurs in bursts. Nusselt numbers, time-averaged over these bursts, vary non-monotonically with 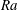$\mathit{Ra}$ for 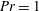$\mathit{Pr}=1$. When the shear is present with 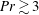$\mathit{Pr}\gtrsim 3$, the flow does not burst, and convective heat transport is sustained at all times. Nusselt numbers then grow roughly as powers of 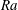$\mathit{Ra}$, but the growth rates are slower than any previously reported for Rayleigh–Bénard convection without large-scale shear. We find that the Nusselt numbers grow proportionally to 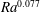$\mathit{Ra}^{0.077}$ when 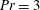$\mathit{Pr}=3$ and to 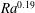$\mathit{Ra}^{0.19}$ when 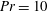$\mathit{Pr}=10$. Analogies with tokamak plasmas are described.

JFM classification

Turbulent Flows: Intermittency MHD and Electrohydrodynamics: Plasmas
Type
Papers
Information
Journal of Fluid Mechanics , Volume 759 , 25 November 2014 , pp. 360 - 385
Check for updates
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahlers, G., Grossmann, S. & Lohse, D. 2009 Heat transfer and large scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81 (2), 503–537.Google Scholar
Ballot, J., Brun, A. S. & Turck-Chièze, S. 2007 Simulations of turbulent convection in rotating young solarlike stars: differential rotation and meridional circulation. Astrophys. J. 669, 1190–1208.CrossRefGoogle Scholar
Bian, N., Benkadda, S., Garcia, O. E., Paulsen, J.-V. & Garbet, X. 2003 The quasilinear behavior of convective turbulence with sheared flows. Phys. Plasmas 10 (5), 1382–1388.CrossRefGoogle Scholar
Bian, N. H. & Garcia, O. E. 2003 Confinement and dynamical regulation in two-dimensional convective turbulence. Phys. Plasmas 10 (12), 4696–4707.CrossRefGoogle Scholar
Brown, B. P., Browning, M. K., Brun, A. S., Miesch, M. S. & Toomre, J. 2008 Rapidly rotating suns and active nests of convection. Astrophys. J. 689 (2), 1354–1372.CrossRefGoogle Scholar
Brummell, N. H. & Hart, J. E. 1993 High Rayleigh number ${\it\beta}$ -convection. Geophys. Astrophys. Fluid Dyn. 68, 85–114.Google Scholar
Busse, F. H. 1983 Generation of mean flows by thermal convection. Physica D 9, 287–299.CrossRefGoogle Scholar
Busse, F. H. 1994 Convection driven zonal flows and vortices in the major planets. Chaos 4 (2), 123–134.CrossRefGoogle ScholarPubMed
Calkins, M. A., Aurnou, J. M., Eldredge, J. D. & Julien, K. 2012 The influence of fluid properties on the morphology of core turbulence and the geomagnetic field. Earth Planet. Sci. Lett. 359–360, 55–60.Google Scholar
Castaing, B., Gunaratne, G., Heslot, F., Kadanoff, L., Libchaber, A., Thomae, S., Wu, X.-Z., Zaleski, S. & Zanetti, G. 1989 Scaling of hard thermal turbulence in Rayleigh–Bénard convection. J. Fluid Mech. 204, 1–30.Google Scholar
Chandrasekhar, S. 1981 Hydrodynamic and Hydromagnetic Stability. Dover.Google Scholar
Childress, S. 2000 Eulerian mean flow from an instability of convective plumes. Chaos 10 (1), 28–38.Google Scholar
Christensen, U. R. 2002 Zonal flow driven by strongly supercritical convection in rotating spherical shells. J. Fluid Mech. 470, 115–133.CrossRefGoogle Scholar
Deardorff, J. W. 1965 Graviational instability between horizontal plates with shear. Phys. Fluids 8 (6), 1027–1030.Google Scholar
Diamond, P. H., Itoh, S.-I., Itoh, K. & Hahm, T. S. 2005 Zonal flows in plasma—a review. Plasma Phys. Control. Fusion 47 (5), R35–R161.CrossRefGoogle Scholar
Domaradzki, J. 1988 Direct numerical simulations of the effects of shear on turbulent Rayleigh–Bénard convection. J. Fluid Mech. 193, 499–531.Google Scholar
Drake, J. F., Finn, J. M., Guzdar, P., Shapiro, V., Shevchenko, V., Waelbroeck, F., Hassam, A. B., Liu, C. S. & Sagdeev, R. 1992 Peeling of convection cells and the generation of sheared flow. Phys. Fluids B 4 (3), 488–491.CrossRefGoogle Scholar
Finn, J. M. 1993 Nonlinear interaction of Rayleigh–Taylor and shear instabilities. Phys. Fluids B 5 (2), 415–432.CrossRefGoogle Scholar
Finn, J. M., Drake, J. F. & Guzdar, P. N. 1992 Instability of fluid vortices and generation of sheared flow. Phys. Fluids B 4 (9), 2758–2768.CrossRefGoogle Scholar
Fisher, P. F., Lottes, J. W. & Kerkemeier, S. G.2014 nek5000 webpage, http://nek5000.mcs.anl.gov.Google Scholar
Fitzgerald, J. G. & Farrell, B. F. 2014 Mechanisms of mean flow formation and suppression in two-dimensional Rayleigh–Bénard convection. Phys. Fluids 26 (5), 054104.CrossRefGoogle Scholar
Gallagher, A. P. & Mercer, A. McD. 1965 On the behaviour of small disturbances in plane Couette flow with a temperature gradient. Proc. R. Soc. Lond. A 286 (1404), 117–128.Google Scholar
Garcia, O. E. & Bian, N. H. 2003 Bursting and large-scale intermittency in turbulent convection with differential rotation. Phys. Rev. E 68 (4), 1–4.Google ScholarPubMed
Garcia, O. E., Bian, N. H., Naulin, V., Nielsen, A. H. & Rasmussen, J. J. 2006 Two-dimensional convection and interchange motions in fluids and magnetized plasmas. Phys. Scr. T122, 104–124.Google Scholar
Garcia, O. E., Bian, N. H., Paulsen, J.-V., Benkadda, S. & Rypdal, K. 2003 Confinement and bursty transport in a flux-driven convection model with sheared flows. Plasma Phys. Control. Fusion 45, 919–932.Google Scholar
Goluskin, D.2013 Zonal flow driven by convection and convection driven by internal heating. PhD thesis, Columbia University.Google Scholar
Grossmann, S. & Lohse, D. 2000 Scaling in thermal convection: a unifying theory. J. Fluid Mech. 407, 27–56.Google Scholar
von Hardenberg, J., Parodi, A., Passoni, G., Provenzale, A. & Spiegel, E. A. 2008 Large-scale patterns in Rayleigh–Bénard convection. Phys. Lett. A 372 (13), 2223–2229.CrossRefGoogle Scholar
Heimpel, M. & Aurnou, J. 2007 Turbulent convection in rapidly rotating spherical shells: a model for equatorial and high latitude jets on Jupiter and Saturn. Icarus 187, 540–557.Google Scholar
Heimpel, M. & Aurnou, J. M. 2012 Convective bursts and the coupling of Saturn’s equatorial storms and interior rotation. Astrophys. J. 746, 1–14.Google Scholar
Hermiz, K. B., Guzdar, P. N. & Finn, J. M. 1995 Improved low-order model for shear flow driven by Rayleigh–Bénard convection. Phys. Rev. E 51 (1), 325–331.Google Scholar
Horton, W., Hu, G. & Laval, G. 1996 Turbulent transport in mixed states of convective cells and sheared flows. Phys. Plasmas 3 (8), 2912–2923.CrossRefGoogle Scholar
Howard, L. N. 1963 Heat transport by turbulent convection. J. Fluid Mech. 17 (3), 405–432.Google Scholar
Howard, L. N. & Krishnamurti, R. 1986 Large-scale flow in turbulent convection: a mathematical model. J. Fluid Mech. 170, 385–410.Google Scholar
Ierley, G. R., Kerswell, R. R. & Plasting, S. C. 2006 Infinite-Prandtl-number convection. Part 2. A singular limit of upper bound theory. J. Fluid Mech. 560, 159–227.CrossRefGoogle Scholar
Ingersoll, A. P. 1966 Convective instabilities in plane Couette flow. Phys. Fluids 9 (4), 682–689.Google Scholar
Johnston, H. & Doering, C. R. 2009 Comparison of turbulent thermal convection between conditions of constant temperature and constant flux. Phys. Rev. Lett. 102 (6), 064501.Google Scholar
Kaspi, Y., Flierl, G. R. & Showman, A. P. 2009 The deep wind structure of the giant planets: results from an anelastic general circulation model. Icarus 202 (2), 525–542.Google Scholar
Knobloch, E. & Moehlis, J. 1999 Bursting mechanisms for hydrodynamical systems. In Pattern Formation in Continuous and Coupled Systems (ed. Golubitsky, M., Luss, D. & Strogatz, S. H.), pp. 157–174. Springer.Google Scholar
Kosloff, D. & Tal-Ezer, H. 1993 A modified Chebyshev pseudospectral method with an $O(N^{-1})$ time step restriction. J. Comput. Phys. 104 (2), 457–469.Google Scholar
Kraichnan, R. H. 1962 Turbulent thermal convection at arbitrary Prandtl number. Phys. Fluids 5 (11), 1374–1389.Google Scholar
Krishnamurti, R. & Howard, L. N. 1981 Large-scale flow generation in turbulent convection. Proc. Natl Acad. Sci. USA 78 (4), 1981–1985.Google Scholar
Leboeuf, J.-N., Charlton, L. A. & Carreras, B. A. 1993 Shear flow effects on the nonlinear evolution of thermal instabilities. Phys. Fluids B 5 (8), 2959–2966.CrossRefGoogle Scholar
Lipps, F. B. 1971 Two-dimensional numerical experiments in thermal convection with vertical shear. J. Atmos. Sci. 28 (1), 3–19.2.0.CO;2>CrossRefGoogle Scholar
Lotka, A. J. 1925 Elements of Physical Biology. Williams and Wilkins Co.Google Scholar
Malkov, M. A., Diamond, P. H. & Rosenbluth, M. N. 2001 On the nature of bursting in transport and turbulence in drift wave–zonal flow systems. Phys. Plasmas 8 (12), 5073–5076.Google Scholar
Malkus, W. V. R. 1954a Discrete transitions in turbulent convection. Proc. R. Soc. Lond. A 225 (1161), 185–195.Google Scholar
Malkus, W. V. R. 1954b The heat transport and spectrum of thermal turbulence. Proc. R. Soc. Lond. A 225 (1161), 196–212.Google Scholar
Massaguer, J. M., Spiegel, E. A. & Zahn, J.-P. 1992 Convection-induced shears for general planforms. Phys. Fluids A 4 (7), 1333–1335.Google Scholar
Matthews, P. C., Rucklidge, A. M., Weiss, N. O. & Proctor, M. R. E. 1996 The three-dimensional development of the shearing instability of convection. Phys. Fluids 8 (6), 1350–1352.CrossRefGoogle Scholar
Morin, V. & Dormy, E. 2004 Time dependent ${\it\beta}$ -convection in rapidly rotating spherical shells. Phys. Fluids 16 (5), 1603–1609.Google Scholar
Otero, J., Wittenberg, R. W., Worthing, R. A. & Doering, C. R. 2002 Bounds on Rayleigh–Bénard convection with an imposed heat flux. J. Fluid Mech. 473, 191–199.CrossRefGoogle Scholar
Parodi, A., von Hardenberg, J., Passoni, G., Provenzale, A. & Spiegel, E. A. 2004 Clustering of plumes in turbulent convection. Phys. Rev. Lett. 92 (19), 194503.CrossRefGoogle ScholarPubMed
Plasting, S. C. & Ierley, G. R. 2005 Infinite-Prandtl-number convection. Part 1. Conservative bounds. J. Fluid Mech. 542, 343–363.CrossRefGoogle Scholar
Platt, N., Spiegel, E. A. & Tresser, C. 1993 On–off intermittency: a mechanism for bursting. Phys. Rev. Lett. 70 (3), 279–282.Google Scholar
van der Poel, E. P., Ostilla-Mónico, R., Verzicco, R. & Lohse, D. 2014 Effect of velocity boundary conditions on the heat transfer and flow topology in two-dimensional Rayleigh–Bénard convection. Phys. Rev. E 90 (1), 013017.Google Scholar
Rucklidge, A. M. & Matthews, P. C. 1996 Analysis of the shearing instability in nonlinear convection and magnetoconvection. Nonlinearity 9, 311–351.Google Scholar
Scagliarini, A., Gylfason, Á. & Toschi, F. 2014 Heat-flux scaling in turbulent Rayleigh–Bénard convection with an imposed longitudinal wind. Phys. Rev. E 89 (4), 043012.Google Scholar
Scott, R. K. & Polvani, L. M. 2007 Forced-dissipative shallow-water turbulence on the sphere and the atmospheric circulation of the giant planets. J. Atmos. Sci. 64 (9), 3158–3176.Google Scholar
Shishkina, O., Stevens, R. J. A. M., Grossmann, S. & Lohse, D. 2010 Boundary layer structure in turbulent thermal convection and its consequences for the required numerical resolution. New J. Phys. 12 (7), 075022.CrossRefGoogle Scholar
Spiegel, E. A. 1971a Convection in stars I. Basic Boussinesq convection. Annu. Rev. Astron. Astrophys. 9, 323–352.Google Scholar
Spiegel, E. A. 1971b Turbulence in stellar convection zones. Comments Astrophys. Space Phys. 3 (2), 53–58.Google Scholar
Spiegel, E. A. & Zaleski, S. 1984 Reaction–diffusion instability in a sheared medium. Phys. Lett. A 106 (7), 335–338.CrossRefGoogle Scholar
Stevens, R. J. A. M., van der Poel, E. P., Grossmann, S. & Lohse, D. 2013 The unifying theory of scaling in thermal convection: the updated prefactors. J. Fluid Mech. 730, 295–308.Google Scholar
Tao, J.-J. & Tan, W.-C. 2010 Relaxation oscillation of thermal convection in rotating cylindrical annulus. Chin. Phys. Lett. 27 (3), 034706.Google Scholar
Taylor, G. 1953 Dispersion of soluble matter in solvent flowing slowly through a tube. Proc. R. Soc. Lond. A 219 (1137), 186–203.Google Scholar
Teed, R. J., Jones, C. A. & Hollerbach, R. 2012 On the necessary conditions for bursts of convection within the rapidly rotating cylindrical annulus. Phys. Fluids 24 (6), 066604.CrossRefGoogle Scholar
Terry, P. W. 2000 Suppression of turbulence and transport by sheared flow. Rev. Mod. Phys. 72 (1), 109–165.Google Scholar
Thompson, R. 1970 Venus’s general circulation is a merry-go-round. J. Atmos. Sci. 27 (8), 1107–1116.2.0.CO;2>CrossRefGoogle Scholar
Wagner, F. 2007 A quarter-century of H-mode studies. Plasma Phys. Control. Fusion 49 (12B), B1–B33.Google Scholar
Werne, J. 1993 Structure of hard-turbulent convection in two dimensions: numerical evidence. Phys. Rev. E 48 (2), 1020–1035.CrossRefGoogle ScholarPubMed
Wesson, J. 2011 Tokamaks, 4th edn. Oxford University Press.Google Scholar
Whitehead, J. P. & Doering, C. R. 2011 Ultimate state of two-dimensional Rayleigh–Bénard convection between free-slip fixed-temperature boundaries. Phys. Rev. Lett. 106 (24), 244501.CrossRefGoogle ScholarPubMed
Whitehead, J. P. & Doering, C. R. 2012 Rigid bounds on heat transport by a fluid between slippery boundaries. J. Fluid Mech. 707, 241–259.CrossRefGoogle Scholar
Wittenberg, R. W. 2010 Bounds on Rayleigh–Bénard convection with imperfectly conducting plates. J. Fluid Mech. 665, 158–198.CrossRefGoogle Scholar
Zaleski, S. 1991 Thermal convection at high Rayleigh numbers in two-dimensional sheared layers. In The Global Geometry of Turbulence (ed. Jiménez, J.), pp. 167–179. Springer.Google Scholar
Zhu, D. & Flierl, G. R.2012 Investigation of vertically sheared flow in fixed-flux turbulent convection. Unpublished manuscript.Google Scholar

Goluskin et al. supplementary movie

Supplement to figure 2(a): Temperature in non-shearing convection with Ra=2•105 and Pr=10. The hottest fluid (red) is one dimensionless degree warmer than the coldest fluid (blue). The dimensionless time span is 0.04.

Download Goluskin et al. supplementary movie(Video)
Video 2.1 MB

Goluskin et al. supplementary movie

Supplement to figure 2(b): Temperature in sustained shearing convection with Ra=2•106 and Pr=10. The hottest fluid (red) is one dimensionless degree warmer than the coldest fluid (blue). The dimensionless time span is 6•10-3.

Download Goluskin et al. supplementary movie(Video)
Video 3.1 MB

Goluskin et al. supplementary movie

Supplement to figure 2(c): Temperature in sustained shearing convection with Ra=2•107 and Pr=10. The hottest fluid (red) is one dimensionless degree warmer than the coldest fluid (blue). The dimensionless time span is 1.2•10-3.

Download Goluskin et al. supplementary movie(Video)
Video 3.1 MB

Goluskin et al. supplementary movie

Supplement to figure 2(d): Temperature in sustained shearing convection with Ra=2•108 and Pr=10. The hottest fluid (red) is one dimensionless degree warmer than the coldest fluid (blue). The dimensionless time span is 2.4•10-4.

Download Goluskin et al. supplementary movie(Video)
Video 3.5 MB

Goluskin et al. supplementary movie

Supplement to figure 8: Temperature in bursting shearing convection with Ra=2•108 and Pr=1. The hottest fluid (red) is one dimensionless degree warmer than the coldest fluid (blue). The time span matches that of the time series shown in the figure.

Download Goluskin et al. supplementary movie(Video)
Video 10 MB