Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-28T18:30:33.277Z Has data issue: false hasContentIssue false
  • English
  • Français

The controlled vertical impact of an inclined flat plate on a quiescent water surface

Published online by Cambridge University Press:  27 September 2019

An Wang Open the ORCID record for An Wang [Opens in a new window]  and
James H. Duncan Open the ORCID record for James H. Duncan [Opens in a new window]
An Wang*
Affiliation:
Department of Mechanical Engineering, University of Maryland, College Park, MD 20742, USA
James H. Duncan
Affiliation:
Department of Mechanical Engineering, University of Maryland, College Park, MD 20742, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The generation of spray during the vertical impact of a flat plate (length 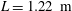$L=1.22~\text{m}$, width 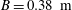$B=0.38~\text{m}$) on a quiescent water surface is studied experimentally. The plate is held in an orientation tilted up from horizontal by angles 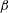$\unicode[STIX]{x1D6FD}$ ranging from 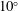$10^{\circ }$ to 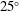$25^{\circ }$ about one of its long edges, which is positioned close to a vertical wall. The plate motion, which is driven by a servo motor system, is set to maintain a constant speed, 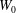$W_{0}$, until the trailing (upper) long edge of the plate passes the still water level (SWL) and then to decelerate to a stop. The impact Froude numbers 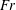$\mathit{Fr}$ (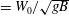$=W_{0}/\sqrt{gB}$, where 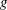$g$ is the gravitational acceleration) range from 0.21 to 0.63. The evolution of the water surface underneath the plate and outboard of its trailing edge is measured with a cinematic laser induced fluorescence technique. As the plate’s leading (low) edge passes the SWL, the local water surface rises and develops into a thin spray sheet that travels along the plate’s lower surface toward the trailing edge. The horizontal speed of the under-plate spray tip is approximately 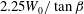$2.25W_{0}/\tan \unicode[STIX]{x1D6FD}$, as high as 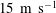$15~\text{m}~\text{s}^{-1}$. In agreement with published similarity theory for the flow during the vertical water entry of a wedge, the under-plate surface profiles scaled by 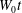$W_{0}t$ nearly collapse on a single curve for each 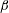$\unicode[STIX]{x1D6FD}$. As the under-plate spray passes the plate’s trailing edge, it develops into the leading portion (called herein the Type I spray) of the outboard spray system. As the trailing edge of the plate passes through the local water surface, a crater develops and a large nearly vertical spray sheet (called the Type II spray) is generated from the outer edge (called the outboard spray root) of the crater. The characteristic horizontal length scale of the crater is found to expand in time following a power law with an exponent of approximately 0.77 for all conditions. A short time after its formation, the outboard spray root becomes the crest of a gravity wave whose propagation speed is of the order of 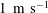$1~\text{m}~\text{s}^{-1}$ for all 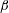$\unicode[STIX]{x1D6FD}$ and 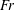$\mathit{Fr}$. The dimensionless envelope of the Type II spray profiles collapse to a single curve at high 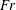$\mathit{Fr}$ for each 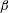$\unicode[STIX]{x1D6FD}$. The connecting spray sheet between the Type I and Type II sprays tends to break up at small 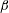$\unicode[STIX]{x1D6FD}$ and large 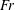$\mathit{Fr}$.

JFM classification

Waves/Free-surface Flows: Surface gravity waves
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 879 , 25 November 2019 , pp. 468 - 511
Check for updates
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bao, C. M., Wu, G. X. & Xu, G. D. 2016 Simulation of water entry of a two-dimension finite wedge with flow detachment. J. Fluids Struct. 65, 44–59.Google Scholar
Bao, C. M., Wu, G. X. & Xu, G. 2017 Simulation of freefall water entry of a finite wedge with flow detachment. Appl. Ocean Res. 65, 262–278.10.1016/j.apor.2017.04.014Google Scholar
Chuang, S.-L.1973 Slamming tests of three-dimensional models in calm water and waves. Tech. Rep. DTIC Document.Google Scholar
Chuang, S.-L. & Milne, D. T.1971 Drop tests of cones to investigate the three-dimensional effects of slamming. Tech. Rep. DTIC Document.Google Scholar
de Divitiis, N. & de Socio, L. M. 2002 Impact of floats on water. J. Fluid Mech. 471, 365–379.Google Scholar
Dobrovol’Skaya, Z. N. 1969 On some problems of similarity flow of fluid with a free surface. J. Fluid Mech. 36 (04), 805–829.Google Scholar
Duez, C., Ybert, C., Clanet, C. & Bocquet, L. 2007 Making a splash with water repellency. Nat. Phys. 3 (3), 180–183.Google Scholar
Faltinsen, O. M. 2005 Hydrodynamics of High-Speed Marine Vehicles. Cambridge University Press.Google Scholar
Faltinsen, O. M., Kvålsvold, J. & Aarsnes, J. V. 1997 Wave impact on a horizontal elastic plate. J. Mar. Sci. Technol. 2 (2), 87–100.Google Scholar
Faltinsen, O. M. & Semenov, Y. A. 2008 Nonlinear problem of flat-plate entry into an incompressible liquid. J. Fluid Mech. 611, 151–173.Google Scholar
Greenhow, M. & Lin, W.-M.1983 Nonlinear-free surface effects: experiments and theory. Tech. Rep. DTIC Document.Google Scholar
Howison, S. D., Ockendon, J. R. & Wilson, S. K. 1991 Incompressible water-entry problems at small deadrise angles. J. Fluid Mech. 222, 215–230.Google Scholar
Huera-Huarte, F. J., Jeon, D. & Gharib, M. 2011 Experimental investigation of water slamming loads on panels. Ocean Engng 38 (11–12), 1347–1355.Google Scholar
Iafrati, A.2012 A fully nonlinear iterative solution method for self-similar potential flows with a free boundary. Preprint, arXiv:1212.6699.Google Scholar
Iafrati, A. 2016 Experimental investigation of the water entry of a rectangular plate at high horizontal velocity. J. Fluid Mech. 799, 637–672.Google Scholar
Iafrati, A. & Korobkin, A. A. 2004 Initial stage of flat plate impact onto liquid free surface. Phys. Fluids 16 (7), 2214–2227.Google Scholar
Iafrati, A. & Korobkin, A. A. 2008 Hydrodynamic loads during early stage of flat plate impact onto water surface. Phys. Fluids 20 (8), 082104.Google Scholar
Iafrati, A. & Korobkin, A. A. 2011 Asymptotic estimates of hydrodynamic loads in the early stage of water entry of a circular disk. J. Engng Maths 69 (2–3), 199–224.10.1007/s10665-010-9411-yGoogle Scholar
Kiara, A., Paredes, R. & Yue, D. K. P. 2017 Numerical investigation of the water entry of cylinders without and with spin. J. Fluid Mech. 814, 131–164.Google Scholar
Korobkin, A. 1994 Blunt-body impact on the free surface of a compressible liquid. J. Fluid Mech. 263, 319–342.10.1017/S0022112094004131Google Scholar
Korobkin, A. A. & Scolan, Y.-M. 2006 Three-dimensional theory of water impact. Part 2. Linearized Wagner problem. J. Fluid Mech. 549, 343–373.Google Scholar
Liu, X. & Duncan, J. H. 2006 An experimental study of surfactant effects on spilling breakers. J. Fluid Mech. 567, 433–455.10.1017/S0022112006002011Google Scholar
Marston, J. O. & Thoroddsen, S. T. 2014 Ejecta evolution during cone impact. J. Fluid Mech. 752, 410–438.Google Scholar
Marston, J. O., Truscott, T. T., Speirs, N. B., Mansoor, M. M. & Thoroddsen, S. T. 2016 Crown sealing and buckling instability during water entry of spheres. J. Fluid Mech. 794, 506–529.Google Scholar
Mayer, H. C. & Krechetnikov, R. 2018 Flat plate impact on water. J. Fluid Mech. 850, 1066–1116.Google Scholar
Moghisi, M. & Squire, P. T. 1981 An experimental investigation of the initial force of impact on a sphere striking a liquid surface. J. Fluid Mech. 108, 133–146.Google Scholar
Oliver, J. M. 2007 Second-order wagner theory for two-dimensional water-entry problems at small deadrise angles. J. Fluid Mech. 572, 59–85.Google Scholar
Peters, I. R., van der Meer, D. & Gordillo, J. M. 2013 Splash wave and crown breakup after disc impact on a liquid surface. J. Fluid Mech. 724, 553–580.Google Scholar
Reinhard, M., Korobkin, A. A. & Cooker, M. J. 2013 Water entry of a flat elastic plate at high horizontal speed. J. Fluid Mech. 724, 123–153.Google Scholar
Scolan, Y.-M. & Korobkin, A. A. 2001 Three-dimensional theory of water impact. Part 1. Inverse Wagner problem. J. Fluid Mech. 440, 293–326.Google Scholar
Semenov, Y. A. & Iafrati, A. 2006 On the nonlinear water entry problem of asymmetric wedges. J. Fluid Mech. 547, 231–256.10.1017/S0022112005007329Google Scholar
Semenov, Y. A. & Wu, G. X. 2016 Water entry of an expanding wedge/plate with flow detachment. J. Fluid Mech. 797, 322–344.Google Scholar
Thoroddsen, S. T., Etoh, T. G., Takehara, K. & Takano, Y. 2004 Impact jetting by a solid sphere. J. Fluid Mech. 499, 139–148.Google Scholar
Thoroddsen, S. T., Thoraval, M.-J., Takehara, K. & Etoh, T. G. 2011 Droplet splashing by a slingshot mechanism. Phys. Rev. Lett. 106 (3), 034501.10.1103/PhysRevLett.106.034501Google Scholar
Truscott, T. T. & Techet, A. H. 2009 Water entry of spinning spheres. J. Fluid Mech. 625, 135–165.Google Scholar
Ulstein, T. & Faltinsen, O. M. 1996 Two-dimensional unsteady planing. J. Ship Res. 40 (3), 200–210.Google Scholar
Vincent, L., Xiao, T., Yohann, D., Jung, S. & Kanso, E. 2018 Dynamics of water entry. J. Fluid Mech. 846, 508–535.Google Scholar
Vorus, W. S. 1996 A flat cylinder theory for vessel impact and steady planing resistance. J. Ship Res. 40 (2), 89–106.Google Scholar
Wagner, H. 1932 Über stoß-und gleitvorgänge an der oberfläche von flüssigkeiten. Z. Angew. Math. Mech. 12 (4), 193–215.Google Scholar
Wang, A., Ikeda-Gilbert, C. M., Duncan, J. H., Lathrop, D. P., Cooker, M. J. & Fullerton, A. M. 2018 The impact of a deep-water plunging breaker on a wall with its bottom edge close to the mean water surface. J. Fluid Mech. 843, 680–721.10.1017/jfm.2018.109Google Scholar
Wang, A., Kim, H.-T., Wong, K. P., Yu, M., Kiger, K. T. & Duncan, J. H. 2019 Spray formation and structural deformation during the oblique impact of a flexible plate on a quiescent water surface. J. Ship Res. 63 (3), 154–164.Google Scholar
Wang, A., Wang, S., Balaras, E., Conroy, D., O’Shea, T. T. & Duncan, J. H. 2016 Spray formation during the impact of a flat plate on a water surface. In Proceedings of the 31st Symposium on Naval Hydrodynamics, Monterey, California, USA, 11–16 September.Google Scholar
Wang, J. & Faltinsen, O. M. 2017 Improved numerical solution of Dobrovol’skaya’s boundary integral equations on similarity flow for uniform symmetrical entry of wedges. Appl. Ocean Res. 66, 23–31.Google Scholar
Wang, J., Lugni, C. & Faltinsen, O. M. 2015a Analysis of loads, motions and cavity dynamics during freefall wedges vertically entering the water surface. Appl. Ocean Res. 51, 38–53.10.1016/j.apor.2015.02.007Google Scholar
Wang, J., Lugni, C. & Faltinsen, O. M. 2015b Experimental and numerical investigation of a freefall wedge vertically entering the water surface. Appl. Ocean Res. 51, 181–203.Google Scholar
Wu, G. X. & Sun, S. L. 2014 Similarity solution for oblique water entry of an expanding paraboloid. J. Fluid Mech. 745, 398–408.Google Scholar
Yakimov, Y. L. 1973 Effect of the atmosphere with the fall of bodies into water. Fluid Dyn. 8 (5), 679–682.Google Scholar
Zhao, R. & Faltinsen, O. 1993 Water entry of two-dimensional bodies. J. Fluid Mech. 246, 593–612.Google Scholar

Wang and Duncan supplementary movie 1

LIF high-speed movie of the under-plate spray evolution for Fr = 0.53, β = 25° (corresponding to figure 5, figure 30).

Download Wang and Duncan supplementary movie 1(Video)
Video 8.2 MB

Wang and Duncan supplementary movie 2

LIF high-speed movie of the outboard spray evolution for Fr = 0.53, β = 20° (corresponding to figure 13).

Download Wang and Duncan supplementary movie 2(Video)
Video 13.3 MB

Wang and Duncan supplementary movie 3

LIF high-speed movie of the under-plate spray evolution for Fr = 0.21, β = 25°

Download Wang and Duncan supplementary movie 3(Video)
Video 5.1 MB

Wang and Duncan supplementary movie 4

LIF high-speed movie of the outboard spray evolution for Fr = 0.53, β = 25° (corresponding to figure 30)

Download Wang and Duncan supplementary movie 4(Video)
Video 12.9 MB

Wang and Duncan supplementary movie 5

LIF high-speed movies of the outboard spray evolution for four values of deadrise angles, β = 10°, 15°, 20° and 25°, all at the same Froude number, Fr = 0.53 (corresponding to figure 34).

Download Wang and Duncan supplementary movie 5(Video)
Video 1.5 MB

Wang and Duncan supplementary movie 6

LIF high-speed movie of the outboard spray evolution for Fr = 0.63, β = 10°.

Download Wang and Duncan supplementary movie 6(Video)
Video 16.4 MB

Wang and Duncan supplementary movie 7

LIF high-speed movie of the outboard spray evolution for Fr = 0.21, β = 25°.

Download Wang and Duncan supplementary movie 7(Video)
Video 9.2 MB