Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-12-01T04:05:19.940Z Has data issue: false hasContentIssue false
  • English
  • Français

Control of stationary cross-flow modes in a Mach 3.5 boundary layer using patterned passive and active roughness

Published online by Cambridge University Press:  08 February 2013

Chan Yong Schuele ,
Thomas C. Corke  and
Eric Matlis
Chan Yong Schuele
Affiliation:
University of Notre Dame, Institute for Flow Physics and Control, Aerospace and Mechanical Engineering Department, Notre Dame, IN 46556, USA
Thomas C. Corke*
Affiliation:
University of Notre Dame, Institute for Flow Physics and Control, Aerospace and Mechanical Engineering Department, Notre Dame, IN 46556, USA
Eric Matlis
Affiliation:
University of Notre Dame, Institute for Flow Physics and Control, Aerospace and Mechanical Engineering Department, Notre Dame, IN 46556, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Spanwise-periodic roughness designed to excite selected wavelengths of stationary cross-flow modes was investigated in a three-dimensional boundary layer at Mach 3.5. The test model was a sharp-tipped 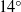$1{4}^{\circ } $ right-circular cone. The model and integrated sensor traversing system were placed in the Mach 3.5 supersonic low disturbance tunnel (SLDT) equipped with an axisymmetric ‘quiet design’ nozzle at NASA Langley Research Center. The model was oriented at a 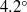$4. {2}^{\circ } $ angle of attack to produce a mean cross-flow velocity component in the boundary layer over the cone. The research examined both passive and active surface roughness. The passive roughness consisted of indentations (dimples) that were evenly spaced around the cone at an axial location that was just upstream of the first linear stability neutral growth branch for cross-flow modes. The active roughness consisted of an azimuthal array of micrometre-sized plasma actuators that were designed to produce the effect of passive surface bumps. Two azimuthal mode numbers of the passive and active patterned roughness were examined. One had an azimuthal mode number that was in the band of initially amplified stationary cross-flow modes. This was intended to represent a controlled baseline condition. The other azimuthal mode number was designed to suppress the growth of the initially amplified stationary cross-flow modes and thereby increase the transition Reynolds number. The results showed that the stationary cross-flow modes were receptive to both the passive and active patterned roughness. Only the passive roughness was investigated at a unit Reynolds number where transition would occur on the cone. Transition front measurements using the Preston tube approach indicated that the transition Reynolds number had increased by 35 % with the subcritical wavenumber roughness compared with the baseline smooth tip cone, and by 40 % compared with the critical wavenumber roughness. Based on the similarities in the response of the stationary cross-flow modes with the active roughness, we expect it would produce a similar transition delay.

JFM classification

Boundary Layers: Boundary Layers Boundary Layers: Boundary layer control Boundary Layers: Boundary layer stability
Type
Papers
Information
Journal of Fluid Mechanics , Volume 718 , 10 March 2013 , pp. 5 - 38
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Balakumar, P. 2009 Stability of supersonic boundary layers on a cone at an angle of attack. In 39th Fluid Dynamics Conference and Exhibit, 22–25 June 2009, San Antonio, TX, paper AIAA-2009-3555.Google Scholar
Beckwith, I. E. 1974 Development of a high Reynolds number quiet tunnel for transition research. AIAA J. 13 (3), 300–306.CrossRefGoogle Scholar
Bippes, H. 1999 Basic experiments on transition in three-dimensional boundary layers dominated by crossflow instability. Prog. Aerosp. 35, 363–412.CrossRefGoogle Scholar
Bonfigli, G. & Kloker, M. 2007 Secondary instability of crossflow vortices: validation of the stability theory by direct numerical simulation. J. Fluid Mech. 583, 229–272.CrossRefGoogle Scholar
Cavalieri, D. 1995 On the experimental design for instability analysis on a cone at Mach 3.5 and 6 using corona discharge pertubation method. MS thesis, Illinois Institute of Technology, Chicago, IL.Google Scholar
Chernoray, V. G., Dovgal, A. V., Kozlov, V. V. & Loefdahl, L. 2005 Experiments on secondary instability of streamwise vortices in a swept-wing boundary layer. J. Fluid Mech. 534, 295–325.Google Scholar
Corke, T. C. 2001 Plasma actuator array development for cross-flow instability control. Internal Report, UND-1-01.Google Scholar
Corke, T., Cavalieri, D. & Matlis, E. 2002 Boundary layer instability on sharp cone at Mach 3.5 with controlled input. AIAA J. 40 (5), 1015–1018.Google Scholar
Corke, T. C., Enloe, C. L. & Wilkinson, S. P. 2010 Dielectric barrier discharge plasma actuators for flow control. Annu. Rev. Fluid Mech. 42, 505–529.CrossRefGoogle Scholar
Corke, T. C. & Knasiak, K. F. 1998 Stationary travelling cross-flow mode interactions on a rotating disk. J. Fluid Mech. 355, 285–315.Google Scholar
Corke, T., Matlis, E. & Othman, H. 2007 Transition to turbulence in rotating-disk boundary layers – convective and absolute instabilities. J. Engng Maths 57, 253–272.Google Scholar
DiCrisitina, V. 1970 Three-dimensional laminar boundary-layer transition on a sharp ${8}^{\circ } $ cone at Mach 10. AIAA J. 8 (5), 852–856.CrossRefGoogle Scholar
Kegerise, M. A., Owens, L. R. & King, R. A. 2010 High-speed boundary-layer transition induced by an isolated roughness element. In 40th Fluid Dynamics Conference and Exhibit, 28 June–1 July, AIAA Paper 2010-4999, Chicago, Illinois.Google Scholar
King, R. A. 1992 Three-dimensional boundary-layer transition on a cone at Mach 3.5. Exp. Fluids 13, 305–314.Google Scholar
Malik, M. R. 1995 eMalik3d: an ${e}^{N} $ code for three-dimensional flow over finite-swept wings. High Technology Report No. HTC-9502.Google Scholar
Matlis, E. H. 2003 Controlled experiments on instabilities and transition to turbulence on a sharp cone at Mach 3.5. PhD thesis, University of Notre Dame, Notre Dame, IN.Google Scholar
Morkovin, M. V. 1990a On roughness-induced transition: facts, views and speculation. In Instability and Transition, vol. I. Springer.Google Scholar
Morkovin, M. V. 1990b Panel summary on roughness. In Instability and Transition, vol. I. Springer.Google Scholar
Radeztsky, R. H. Jr., Reibert, M. S. & Saric, W. S. 1999 Effect of isolated micron-sized roughness on transition in swept-wing flows. AIAA J. 37 (11), 1370–1377.Google Scholar
Reed, H. L. & Saric, W. S. 1989 Stability of three-dimensional boundary layers. Annu. Rev. Fluid Mech. 21, 235–284.CrossRefGoogle Scholar
Reibert, M. S. 1996 Nonlinear stability, saturation, and transition in crossflow-dominated boundary layers. PhD thesis, Arizona State University.Google Scholar
Reshotko, E. 2008 Paths to taransition wall layers. Papers presented during the AVT-151 RTO AVT/VKI Lecture Series held at the von Kármán Institute, Rhode St. Gense, Belgium, 9–12 June.Google Scholar
Saric, W. S., Carrillo, R. B. & Reibert, M. S. 1998a Nonlinear stability and transition in 3-D boundary layers. Meccanica 33, 469–187.CrossRefGoogle Scholar
Saric, W. S. & Reed, H. L. 2002 Supersonic laminar flow control on swept wings using distributed roughness. AIAA Paper 2002-0147.Google Scholar
Saric, W. S. & Reed, H. L. 2003 Crossflow instabilities-theory and technology. AIAA Paper 2003-0771.Google Scholar
Saric, W. S., Reed, H. L. & Banks, D. W. 2004 Flight testing of laminar flow control in high-speed boundary layers. Paper presented at the RTO AVT Specialists’ Meeting on ‘Enhancement of NATO Military Flight Vehicle Performance by Managemenet of Interacting Boundary Layer Transition and Separation’, held in Prague, Czech Republic, 4–7 October 2004, published in RTO-MP-AVT-111.Google Scholar
Saric, W. S., Reed, H. L. & Kerschen, E. J. 2002 Boundary-layer receptivity to freestream disturbances. Annu. Rev. Fluid Mech. 34, 291–319.Google Scholar
Saric, W. S., Reed, H. L. & White, E. B. 2003 Stability and transition of three-dimensional boundary layers. Annu. Rev. Fluid Mech. 35, 413–440.Google Scholar
Saric, W. S., Ruben, C. C. & Reibert, M. S. 1998b Leading-edge roughness as a transition control mechanism. AIAA Paper AIAA-98-0781.Google Scholar
Schuele, C.-Y. 2011 Control of stationary cross-flow modes in a Mach 3.5 boundary layer using passive and active roughness. PhD thesis, University of Notre Dame, Notre Dame, IN.CrossRefGoogle Scholar
Semionov, N. V. & Kosinov, A. D. 2007 Method laminar-turbulent transition control of supersonic boundary layer on a swept wing. Thermophys. Aeromech. 14 (3), 337–341.Google Scholar
Semionov, N. V., Kosinov, A. D. & Levchenko, V. Ya. 2006 Experimental study of turbulence beginning and transition control in a supersonic boundary layer on swept wing. In Sixth IUTAM Symposium on Laminar Turbulent Transition (R. Govindarajan), pp. 355–361, Fluid Mechanics and Its Applications, Vol. 78, ISBN 978-1-4020-3459-6.Google Scholar
Stetson, K. F. 1980 Hypersonic boundary layer transition experiments. Air Force Wright Aeronautical Laboratories Technical Report AFWAL-TR-80-3062.Google Scholar
Valerioti, J. 2010 Pressure dependence of plasma actuated flow control. MS thesis, University of Notre Dame, Notre Dame, IN.Google Scholar
Wasserman, P. & Kloker, M. 2002 Mechanisms and passive control of crossflow-vortex-induced transition in a three-dimensional boundary layer. J. Fluid Mech. 456, 49–84.Google Scholar
White, E. & Saric, W. 2000 Application of variable leading-edge roughness for transition control on swept wings. In AIAA Paper 2000-0283.Google Scholar
White, E. B. & Saric, W. S. 2005 Secondary instability of crossflow vortices. J. Fluid Mech. 525, 275–308.Google Scholar
Wilkinson, S. P., Anders, S. G., Chen, F. J. & Beckwith, I. E. 1992 Supersonic and hypersonic quiet tunnel technology at NASA langley. In AIAA 17 Aerospace Ground Testing Conference, Nashville, TN.CrossRefGoogle Scholar
Wolf, S. W. D. & Laub, J. A. 1997 NASA Ames Laminar Flow Supersonic WInd Tunnel (LFSWT) Tests of a $1{0}^{\circ } $ Cone at Mach 1.6. NASA Technical Memorandum NASA-TM 110438.Google Scholar