Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Pan, Bin
Yin, Xia
and
Iglauer, Stefan
2021.
Rock-fluid interfacial tension at subsurface conditions: Implications for H2, CO2 and natural gas geo-storage.
International Journal of Hydrogen Energy,
Vol. 46,
Issue. 50,
p.
25578.
Pan, Bin
Yin, Xia
Ju, Yang
and
Iglauer, Stefan
2021.
Underground hydrogen storage: Influencing parameters and future outlook.
Advances in Colloid and Interface Science,
Vol. 294,
Issue. ,
p.
102473.
McClure, James E.
Berg, Steffen
and
Armstrong, Ryan T.
2021.
Capillary fluctuations and energy dynamics for flow in porous media.
Physics of Fluids,
Vol. 33,
Issue. 8,
Chen, R.
Chen, Y.
Xu, W.
Hu, Y.
Zhan, L.
Li, J.
Zhuang, D.
and
Li, K.
2022.
The Influence of the Hypergravity Field During Bubble Ripening in Porous Media.
Geophysical Research Letters,
Vol. 49,
Issue. 10,
Mehmani, Yashar
and
Xu, Ke
2022.
Pore-network modeling of Ostwald ripening in porous media: How do trapped bubbles equilibrate?.
Journal of Computational Physics,
Vol. 457,
Issue. ,
p.
111041.
Mehmani, Yashar
and
Xu, Ke
2022.
Capillary equilibration of trapped ganglia in porous media: A pore-network modeling approach.
Advances in Water Resources,
Vol. 166,
Issue. ,
p.
104223.
Pan, Bin
Yin, Xia
Zhu, Weiyao
Yang, Yongfei
Ju, Yang
Yuan, Yujie
zhang, Lijie
and
Iglauer, Stefan
2022.
Theoretical study of brine secondary imbibition in sandstone reservoirs: Implications for H2, CH4, and CO2 geo-storage.
International Journal of Hydrogen Energy,
Vol. 47,
Issue. 41,
p.
18058.
Feng, Yitian
Wang, Chuanxi
Jin, Xu
and
Xu, Ke
2022.
Comprehensive Darcy-Scale Analysis of Ripening in Porous Media.
Transport in Porous Media,
Vol. 144,
Issue. 1,
p.
301.
Li, Yaxin
Orr, Franklin M.
and
Benson, Sally M.
2022.
Long-Term Redistribution of Residual Gas Due to Non-convective Transport in the Aqueous Phase.
Transport in Porous Media,
Vol. 141,
Issue. 1,
p.
231.
Singh, Deepak
Friis, Helmer André
Jettestuen, Espen
and
Helland, Johan Olav
2022.
A level set approach to Ostwald ripening of trapped gas bubbles in porous media.
Transport in Porous Media,
Vol. 145,
Issue. 2,
p.
441.
Blunt, Martin J.
2022.
Ostwald ripening and gravitational equilibrium: Implications for long-term subsurface gas storage.
Physical Review E,
Vol. 106,
Issue. 4,
Chen, Xiao-Peng
Feng, Jun-Peng
Hu, Hai-Bao
Du, Peng
and
Wang, Ti-Kang
2022.
Lattice Boltzmann method based simulation of two dimensional bubble group ripening process.
Acta Physica Sinica,
Vol. 71,
Issue. 11,
p.
110504.
Yu, Wei
and
Kanj, Mazen Y.
2022.
Review of foam stability in porous media: The effect of coarsening.
Journal of Petroleum Science and Engineering,
Vol. 208,
Issue. ,
p.
109698.
Picchi, D.
and
Poesio, P.
2022.
Dispersion of a passive scalar around a Taylor bubble.
Journal of Fluid Mechanics,
Vol. 951,
Issue. ,
Yu, Yuehongjiang
Wang, Chuanxi
Liu, Junning
Mao, Sheng
Mehmani, Yashar
and
Xu, Ke
2023.
Bubble Coarsening Kinetics in Porous Media.
Geophysical Research Letters,
Vol. 50,
Issue. 1,
Zhang, Mu-An
Wang, Jin-Qing
Wu, Rui
Feng, Zhi
Zhan, Ming-Xiu
Xu, Xu
and
Chi, Zuo-He
2023.
Three-dimensional numerical simulation of Ostwald ripening characteristics of bubbles in porous medium.
Acta Physica Sinica,
Vol. 72,
Issue. 16,
p.
164701.
Bueno, Nicolas
Ayala, Luis
and
Mehmani, Yashar
2023.
Ostwald ripening of multi-component bubbles in porous media: A theory and a pore-scale model of how bubble populations equilibrate.
Advances in Water Resources,
Vol. 182,
Issue. ,
p.
104581.
Huang, Ruotong
Herring, Anna L.
and
Sheppard, Adrian
2023.
Investigation of supercritical CO2 mass transfer in porous media using X-ray micro-computed tomography.
Advances in Water Resources,
Vol. 171,
Issue. ,
p.
104338.
Singh, Deepak
Friis, Helmer André
Jettestuen, Espen
and
Helland, Johan Olav
2023.
Pore-scale Ostwald ripening of gas bubbles in the presence of oil and water in porous media.
Journal of Colloid and Interface Science,
Vol. 647,
Issue. ,
p.
331.
Joewondo, Nerine
Garbin, Valeria
and
Pini, Ronny
2023.
Experimental evidence of the effect of solute concentration on the collective evolution of bubbles in a regular pore-network.
Chemical Engineering Research and Design,
Vol. 192,
Issue. ,
p.
82.
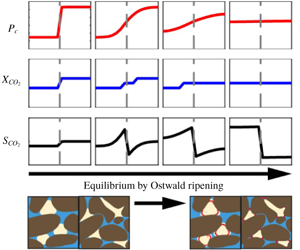
 $10^{5}$ times slower than a single-phase diffusion problem due to the fact that separate-phase gas requires a much larger amount of mass transfer before equilibrium is established. An approximate solution has been developed to predict the saturation redistribution between the two media. The model has been validated by numerical simulation over a wide range of physical parameters. Millimetre to centimetre-scale systems come to equilibrium in years, ranging up to 10 000 years and longer for metre-scale systems. These findings are particularly relevant for geological
$10^{5}$ times slower than a single-phase diffusion problem due to the fact that separate-phase gas requires a much larger amount of mass transfer before equilibrium is established. An approximate solution has been developed to predict the saturation redistribution between the two media. The model has been validated by numerical simulation over a wide range of physical parameters. Millimetre to centimetre-scale systems come to equilibrium in years, ranging up to 10 000 years and longer for metre-scale systems. These findings are particularly relevant for geological  $\text{CO}_{2}$ storage, where residual trapping is an important mechanism for immobilizing
$\text{CO}_{2}$ storage, where residual trapping is an important mechanism for immobilizing  $\text{CO}_{2}$. Our work demonstrates that Ostwald ripening due to heterogeneity in porous media is slow and on a similar time scale compared to other processes that redistribute trapped
$\text{CO}_{2}$. Our work demonstrates that Ostwald ripening due to heterogeneity in porous media is slow and on a similar time scale compared to other processes that redistribute trapped  $\text{CO}_{2}$ such as convective mixing.
$\text{CO}_{2}$ such as convective mixing.

