Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Daviet, Gilles
and
Bertails-Descoubes, Florence
2016.
A semi-implicit material point method for the continuum simulation of granular materials.
ACM Transactions on Graphics,
Vol. 35,
Issue. 4,
p.
1.
Daviet, Gilles
and
Bertails-Descoubes, Florence
2016.
Nonsmooth simulation of dense granular flows with pressure-dependent yield stress.
Journal of Non-Newtonian Fluid Mechanics,
Vol. 234,
Issue. ,
p.
15.
Clark, Abram H.
Kondic, Lou
and
Behringer, Robert P.
2016.
Steady flow dynamics during granular impact.
Physical Review E,
Vol. 93,
Issue. 5,
Maiti, Ritwik
Das, Gargi
and
Das, Prasanta Kumar
2016.
Experiments on eccentric granular discharge from a quasi-two-dimensional silo.
Powder Technology,
Vol. 301,
Issue. ,
p.
1054.
Fei, Minglong
Sun, Qicheng
Xu, Xiaorong
Jin, Feng
and
Zhou, Gordon G.D.
2016.
Simulations of multi-states properties of granular materials based on non-linear granular elasticity and the MiDi rheological relation.
Powder Technology,
Vol. 301,
Issue. ,
p.
1092.
Thomas, C. C.
and
Durian, D. J.
2016.
Intermittency and velocity fluctuations in hopper flows prone to clogging.
Physical Review E,
Vol. 94,
Issue. 2,
Kamrin, Ken
Radjai, F.
Nezamabadi, S.
Luding, S.
and
Delenne, J.Y.
2017.
A hierarchy of granular continuum models: Why flowing grains are both simple and complex.
EPJ Web of Conferences,
Vol. 140,
Issue. ,
p.
01007.
Wang, Chun
Wang, Yongqi
Peng, Chong
and
Meng, Xiannan
2017.
Two-fluid smoothed particle hydrodynamics simulation of submerged granular column collapse.
Mechanics Research Communications,
Vol. 79,
Issue. ,
p.
15.
Tampubolon, Andre Pradhana
Gast, Theodore
Klár, Gergely
Fu, Chuyuan
Teran, Joseph
Jiang, Chenfanfu
and
Museth, Ken
2017.
Multi-species simulation of porous sand and water mixtures.
ACM Transactions on Graphics,
Vol. 36,
Issue. 4,
p.
1.
Maiti, Ritwik
Das, Gargi
and
Das, Prasanta Kumar
2017.
Granular drainage from a quasi-2D rectangular silo through two orifices symmetrically and asymmetrically placed at the bottom.
Physics of Fluids,
Vol. 29,
Issue. 10,
Fullard, Luke
and
Davies, Clive
2017.
Minimising the spread of residence-time distribution for flat and heaped powders in a wedge-shaped planar hopper.
Particuology,
Vol. 30,
Issue. ,
p.
102.
Dunatunga, Sachith
and
Kamrin, Ken
2017.
Continuum modeling of projectile impact and penetration in dry granular media.
Journal of the Mechanics and Physics of Solids,
Vol. 100,
Issue. ,
p.
45.
Koivisto, Juha
and
Durian, Douglas J.
2017.
The sands of time run faster near the end.
Nature Communications,
Vol. 8,
Issue. 1,
Liu, Daren
and
Henann, David L.
2017.
Non-local continuum modelling of steady, dense granular heap flows.
Journal of Fluid Mechanics,
Vol. 831,
Issue. ,
p.
212.
Koivisto, Juha
Korhonen, Marko
Alava, Mikko
Ortiz, Carlos P.
Durian, Douglas J.
and
Puisto, Antti
2017.
Friction controls even submerged granular flows.
Soft Matter,
Vol. 13,
Issue. 41,
p.
7657.
Hurley, Ryan C.
and
Andrade, José E.
2017.
Continuum modeling of rate-dependent granular flows in SPH.
Computational Particle Mechanics,
Vol. 4,
Issue. 1,
p.
119.
Xu, Tibing
Jin, Yee-Chung
Tai, Yih-Chin
and
Lu, Chun-Hua
2017.
Simulation of velocity and shear stress distributions in granular column collapses by a mesh-free method.
Journal of Non-Newtonian Fluid Mechanics,
Vol. 247,
Issue. ,
p.
146.
Zhou, Y.
Lagrée, P.-Y.
Popinet, S.
Ruyer, P.
and
Aussillous, P.
2017.
Experiments on, and discrete and continuum simulations of, the discharge of granular media from silos with a lateral orifice.
Journal of Fluid Mechanics,
Vol. 829,
Issue. ,
p.
459.
Yue, Yonghao
Smith, Breannan
Chen, Peter Yichen
Chantharayukhonthorn, Maytee
Kamrin, Ken
and
Grinspun, Eitan
2018.
Hybrid grains.
ACM Transactions on Graphics,
Vol. 37,
Issue. 6,
p.
1.
Gao, Ming
Pradhana, Andre
Han, Xuchen
Guo, Qi
Kot, Grant
Sifakis, Eftychios
and
Jiang, Chenfanfu
2018.
Animating fluid sediment mixture in particle-laden flows.
ACM Transactions on Graphics,
Vol. 37,
Issue. 4,
p.
1.
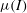 ${\it\mu}(I)$ inertial rheology of granular materials. When the free volume exceeds a critical level, the material is deemed to separate and is treated as disconnected, stress-free media. A material point method (MPM) procedure is written for the simulation of this model and many demonstrations are provided in different geometries, which highlight the ability of the numerical model to handle transitions through dense and disconnected states. By using the MPM framework, extremely large strains and nonlinear deformations, which are common in granular flows, are representable. The method is verified numerically and its physical predictions are validated against many known experimental phenomena, such as Beverloo’s scaling in silo flows, jointed power-law scaling of the run-out distance in granular-column-collapse problems, and various known behaviours in inclined chute flows.
${\it\mu}(I)$ inertial rheology of granular materials. When the free volume exceeds a critical level, the material is deemed to separate and is treated as disconnected, stress-free media. A material point method (MPM) procedure is written for the simulation of this model and many demonstrations are provided in different geometries, which highlight the ability of the numerical model to handle transitions through dense and disconnected states. By using the MPM framework, extremely large strains and nonlinear deformations, which are common in granular flows, are representable. The method is verified numerically and its physical predictions are validated against many known experimental phenomena, such as Beverloo’s scaling in silo flows, jointed power-law scaling of the run-out distance in granular-column-collapse problems, and various known behaviours in inclined chute flows.


