Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-02T21:17:30.715Z Has data issue: false hasContentIssue false
  • English
  • Français

Connections between the Ozmidov scale and mean velocity profile in stably stratified atmospheric surface layers

Published online by Cambridge University Press:  24 May 2016

Dan Li ,
Scott T. Salesky  and
Tirtha Banerjee
Dan Li*
Affiliation:
Department of Earth and Environment, Boston University, Boston, MA 02215, USA
Scott T. Salesky
Affiliation:
Department of Civil Engineering, University of British Columbia, Vancouver, BC V6T 1Z4, Canada
Tirtha Banerjee
Affiliation:
Karlsruhe Institute of Technology (KIT), Institute of Meteorology and Climate Research, Atmospheric Environment Research (IMK-IFU), Garmisch-Partenkirchen, Bavaria 82467, Germany
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The mean velocity profile (MVP) in thermally stratified atmospheric surface layers (ASLs) deviates from the classic logarithmic form. A theoretical framework was recently proposed (Katul et al.Phys. Rev. Lett., vol. 107, 2011, 268502) to link the MVP to the spectrum of turbulence and was found to successfully predict the MVP for unstable stratification. However, the theory failed to reproduce the MVP in stable conditions (Salesky et al.Phys. Fluids, vol. 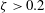25, 2013, 105101), especially when ${\it\zeta}>0.2$ (where 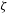${\it\zeta}$ is the atmospheric stability parameter). In the present study, it is demonstrated that this shortcoming is due to the failure to identify the appropriate length scale that characterizes the size of momentum transporting eddies in the stable ASL. Beyond 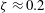${\it\zeta}\approx 0.2$ (near where the original theory fails), the Ozmidov length scale becomes smaller than the distance from the wall $z$ and hence is a more stringent constraint for characterizing the size of turbulent eddies. An expression is derived to connect the Ozmidov length scale to the normalized MVP (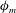${\it\phi}_{m}$), allowing 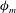${\it\phi}_{m}$ to be solved numerically. It is found that the revised theory produces a prediction of 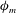${\it\phi}_{m}$ in good agreement with the widely used empirical Businger–Dyer relation and two experimental datasets in the stable ASL. The results here demonstrate that the behaviour of 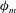${\it\phi}_{m}$ in the stable ASL is closely linked to the size of momentum transporting eddies, which can be characterized by the Ozmidov scale under mildly to moderately stable conditions (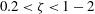$0.2<{\it\zeta}<1-2$).

JFM classification

Geophysical and Geological Flows: Atmospheric flows Turbulent Flows: Stratified turbulence Turbulent Flows: Turbulent boundary layers
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 797 , 25 June 2016 , R3
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Banerjee, T. & Katul, G. G. 2013 Logarithmic scaling in the longitudinal velocity variance explained by a spectral budget. Phys. Fluids 25, 125106.CrossRefGoogle Scholar
Banerjee, T., Katul, G. G., Salesky, S. T. & Chamecki, M. 2015 Revisiting the formulations for the longitudinal velocity variance in the unstable atmospheric surface layer. Q. J. R. Meterol. Soc. 141 (690), 1699–1711.CrossRefGoogle Scholar
Banerjee, T., Li, D., Juang, J. Y. & Katul, G. G. 2016 A spectral budget model for the longitudinal turbulent velocity in the stable atmospheric surface layer. J. Atmos. Sci. 73 (1), 145–166.CrossRefGoogle Scholar
Bou-Zeid, E., Higgins, C., Huwald, H., Meneveau, C. & Parlange, M. B. 2010 Field study of the dynamics and modelling of subgrid scale turbulence in a stable atmospheric surface layer over a glacier. J. Fluid Mech. 665, 480–515.CrossRefGoogle Scholar
Businger, J. A. 1988 A note on the Businger–Dyer profiles. Boundary-Layer Meteorol. 42 (1), 145–151.CrossRefGoogle Scholar
Businger, J. A., Wyngaard, J. C., Izumi, Y. & Bradley, E. F. 1971 Flux-profile relationships in the atmospheric surface layer. J. Atmos. Sci. 28 (2), 181–191.Google Scholar
Businger, J. A. & Yaglom, A. M. 1971 Introduction to Obukhov’s paper on ‘Turbulence in an atmosphere with a non-uniform temperature’. Boundary-Layer Meteorol. 2, 3–6.Google Scholar
Dougherty, J. P. 1961 The anisotropy of turbulence at the meteor level. J. Atmos. Terr. Phys. 21 (2–3), 210–213.CrossRefGoogle Scholar
Dyer, A. J. 1974 A review of flux-profile relationships. Boundary-Layer Meteorol. 7 (3), 363–372.Google Scholar
Esau, I. N. & Grachev, A. A. 2007 Turbulent Prandtl number in stably stratified atmospheric boundary layer: intercomparison between LES and SHEBA data. e-Wind Eng. 005, 1–17.Google Scholar
Gioia, G., Guttenberg, N., Goldenfeld, N. & Chakraborty, P. 2010 Spectral theory of the turbulent mean-velocity profile. Phys. Rev. Lett. 105, 184501.Google Scholar
Grachev, A. A., Andreas, E. L., Fairall, C. W., Guest, P. S. & Persson, P. O. G. 2007 On the turbulent Prandtl number in the stable atmospheric boundary layer. Boundary-Layer Meteorol. 125 (2), 329–341.Google Scholar
Grachev, A. A., Andreas, E. L., Fairall, C. W., Guest, P. S. & Persson, P. O. G. 2013 The critical Richardson number and limits of applicability of local similarity theory in the stable boundary layer. Boundary-Layer Meteorol. 147 (1), 51–82.CrossRefGoogle Scholar
Grachev, A. A., Andreas, E. L., Fairall, C. W., Guest, P. S. & Persson, P. O. G. 2015 Similarity theory based on the Dougherty–Ozmidov length scale. Q. J. R. Meterol. Soc. 141 (690), 1845–1856.CrossRefGoogle Scholar
Högström, U. L. F. 1988 Non-dimensional wind and temperature profiles in the atmospheric surface layer: a re-evaluation. In Topics in Micrometeorology. A Festschrift for Arch Dyer, pp. 55–78. Springer.Google Scholar
Katul, G. G., Konings, A. G. & Porporato, A. 2011 Mean velocity profile in a sheared and thermally stratified atmospheric boundary layer. Phys. Rev. Lett. 107, 268502.CrossRefGoogle Scholar
Katul, G. G., Li, D., Chamecki, M. & Bou-Zeid, E. 2013 Mean scalar concentration profile in a sheared and thermally stratified atmospheric surface layer. Phys. Rev. E 87 (2), 023004.Google Scholar
Katul, G. G., Porporato, A., Shah, S. & Bou-Zeid, E. 2014 Two phenomenological constants explain similarity laws in stably stratified turbulence. Phys. Rev. E 89 (1), 023007.Google Scholar
Li, D. & Bou-Zeid, E. 2011 Coherent structures and the dissimilarity of turbulent transport of momentum and scalars in the unstable atmospheric surface layer. Boundary-Layer Meteorol. 140 (2), 243–262.Google Scholar
Li, D., Bou-Zeid, E. & de Bruin, H. 2012 Monin–Obukhov similarity functions for the structure parameters of temperature and humidity. Boundary-Layer Meteorol. 145 (1), 45–67.CrossRefGoogle Scholar
Li, D., Katul, G. G. & Bou-Zeid, E. 2015a Turbulent energy spectra and cospectra of momentum and heat fluxes in the stable atmospheric surface layer. Boundary-Layer Meteorol. 157 (1), 1–21.Google Scholar
Li, D., Katul, G. G. & Gentine, P. 2016 The k -1 scaling of air temperature spectra in atmospheric surface layer flows. Q. J. R. Meterol. Soc. 142, 496–505.Google Scholar
Li, D., Katul, G. G. & Zilitinkevich, S. S. 2015b Revisiting the turbulent Prandtl number in an idealized atmospheric surface layer. J. Atmos. Sci. 72 (6), 2394–2410.Google Scholar
Mahrt, L. 2014 Stably stratified atmospheric boundary layers. Ann. Rev. Fluid Mech. 46, 23–45.CrossRefGoogle Scholar
Mater, B. D., Schaad, S. M. & Venayagamoorthy, S. K. 2013 Relevance of the Thorpe length scale in stably stratified turbulence. Phys. Fluids 25 (7), 076604.Google Scholar
Monin, A. S. & Obukhov, A. M. 1954 Basic laws of turbulent mixing in the ground layer of the atmosphere. Akad. Nauk. SSSR Geofiz. Inst. Trudy 151, 163–187.Google Scholar
Obukhov, A. M. 1946 Turbulence in thermally inhomogeneous atmosphere. Trudy Inta Teoret. Geofiz. Akad. Nauk. SSSR 1, 95–115.Google Scholar
Ozmidov, R. V. 1965 On the turbulent exchange in a stably stratified ocean. Izv. Acad. Sci. USSR Atmos. Oceanic Phys 1, 861–871.Google Scholar
Salesky, S. T. & Chamecki, M. 2012 Random errors in turbulence measurements in the atmospheric surface layer: implications for Monin–Obukhov similarity theory. J. Atmos. Sci. 69 (12), 3700–3714.Google Scholar
Salesky, S. T., Katul, G. G. & Chamecki, M. 2013 Buoyancy effects on the integral length scales and mean velocity profile in atmospheric surface layer flows. Phys. Fluids 25 (10), 105101.CrossRefGoogle Scholar
Smyth, W. D. & Moum, J. N. 2000 Length scales of turbulence in stably stratified mixing layers. Phys. Fluids 12 (6), 1327–1342.CrossRefGoogle Scholar
Sorbjan, Z. 2008 Gradient-based similarity in the atmospheric boundary layer. Acta Geophys. 56 (1), 220–233.Google Scholar
Sorbjan, Z. 2010 Gradient-based scales and similarity laws in the stable boundary layer. Q. J. R. Meterol. Soc. 136 (650), 1243–1254.Google Scholar
Stull, R. B. 1988 An Introduction to Boundary Layer Meteorology. Kluwer.Google Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow. vol. 1, p. 438. Cambridge University Press.Google Scholar
Vercauteren, N., Bou-Zeid, E., Parlange, M. B., Lemmin, U., Huwald, H., Selker, J. & Meneveau, C. 2008 Subgrid-scale dynamics for water vapor, heat, and momentum over a lake. Boundary-Layer Meteorol. 128 (2), 205–228.CrossRefGoogle Scholar
Zilitinkevich, S. S. & Calanca, P. 2000 An extended similarity theory for the stably stratified atmospheric surface layer. Q. J. R. Meterol. Soc. 126 (566), 1913–1923.CrossRefGoogle Scholar