Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-12-03T00:39:03.770Z Has data issue: false hasContentIssue false
  • English
  • Français

Compressible vapour flow in conduits and fractures

Published online by Cambridge University Press:  10 August 2016

Herbert E. Huppert  and
R. Stephen Sparks
Herbert E. Huppert*
Affiliation:
Institute of Theoretical Geophysics, Department of Applied Mathematics and Theoretical Physics, University of Cambridge, CB3 0WA, UK Faculty of Science, University of Bristol, BS8 1RJ, UK School of Mathematics and Statistics, University of New South Wales, Sydney, NSW 2052, Australia Department of Earth Sciences, University of Bristol, BS8 1RJ, UK
R. Stephen Sparks
Affiliation:
Department of Earth Sciences, University of Bristol, BS8 1RJ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the steady flow of a viscous compressible gas through an axisymmetric or two-dimensional porous medium whose properties in the direction of the flow are sufficiently slowly varying. The study is partly motivated by a number of different applications in the Earth sciences, including the release of magmatic volatiles from a magma chamber beneath an active volcano and the discharge of geothermal fluids. The results are also relevant to evaluating the consequences of an accidental release of carbon dioxide from a storage reservoir within the Earth, as might happen at a carbon capture and storage (CCS) site. We consider both slow, thermally equilibrated, flows and fast, adiabatic flows. Because the flow is compressible, it is the mass (and not the volume) flux which is conserved along the flow. We determine this constant mass flux and the velocity and pressure fields, both of which vary with position along the flow, as a function of all the physical parameters. We find that the resultant pressure gradient in the medium is largest at the far, low-pressure end of the conduit because the velocity is largest at that end due to the smallest density being associated with the smallest pressures. This means that the pressure in the permeable conduit is always larger than the linear pressure distribution which joins the given pressures at depth and at the surface, as would be the situation if the flow were incompressible. The detailed pressure distribution is shown to depend on the variation with depth of the quantity 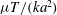$\unicode[STIX]{x1D707}T/(ka^{2})$, where 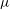$\unicode[STIX]{x1D707}$ is the dynamic viscosity of the vapour, 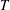$T$ is the external temperature, 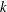$k$ the permeability and 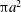$\unicode[STIX]{x03C0}a^{2}$ the cross-sectional area of the conduit. The resultant mass flux is determined to be proportional to the mean along the flow of 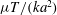$\unicode[STIX]{x1D707}T/(ka^{2})$. We present two numerical illustrations of the results.

JFM classification

Compressible Flows: Compressible Flows Compressible Flows: Gas dynamics Geophysical and Geological Flows: Geophysical and Geological Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 802 , 10 September 2016 , pp. 750 - 759
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bear, J. 1972 Dynamics of Fluids in Porous Media. Dover.Google Scholar
Blundy, J., Mavrogenes, J., Tattich, B., Sparks, R. S. J. & Gilmer, A. 2015 Generation of porphyry copper deposits by gas-brine reaction in volcanic acres. Nat. Geosci. 8, 235–240.Google Scholar
Christopher, T., Humphreys, M. C. S., Barclay, J., Genareau, K., de Angelis, S. M. H., Plail, M. & Donovan, A. 2014 Petrological and geochemical variation during the Soufriere Hills eruption, 1995 to 2010. In The Eruption of Soufrire Hills Volcano, Montserrat from 2000 to 2010 (ed. Wadge, G., Robertson, R. E. A. & Voight, B.), Memoirs, vol. 39, pp. 317–342. Geological Society.Google Scholar
Dullien, F. A. L. 1991 Porous Media, Fluid Transport and Pore Structure. Springer.Google Scholar
Edmonds, M. 2008 New geochemical insights into volcanic degassing. Phil. Trans. R. Soc. Lond. A 366, 4559–4579.Google ScholarPubMed
Huppert, H. E. & Neufeld, J. A. 2014 The fluid mechanics of carbon dioxide sequestration. Annu. Rev. Fluid Mech. 46, 255–272.Google Scholar
Kling, G. W., Clark, M., Compton, H. R., Devine, J. D., Evans, W. C., Humphrey, A. M., Lockwood, J. P. & Tuttle, M. L. 1987 The Lake Nyos gas disaster in Cameroon, West Africa. Science 236, 169–175.CrossRefGoogle ScholarPubMed
Kuang, X. & Jiao, J. J. 2014 An integrated permeability-depth model for Earth’s crust. Geophys. Res. Lett 41, 7539–7545.Google Scholar
Melnik, O. & Sparks, R. S. J. 1999 Nonlinear dynamics of lava dome extrusion. Nature 402, 37–41.CrossRefGoogle Scholar
Mueller, S., Melnik, O., Spider, O., Scheu, B. & Dingwell, D. B. 2008 Permeability and degassing of dome lavas undergoing rapid decompression: an experimental determination. Bull. Volcanol. 67, 526–538.CrossRefGoogle Scholar
Neufeld, J. A., Vella, D. & Huppert, H. E. 2009 The effect of a fissure on storage in a porous medium. J. Fluid Mech. 639, 239–259.CrossRefGoogle Scholar
Phillips, O. 1991 Flow and Reactions in Porous Media. Cambridge University Press.Google Scholar
Pinder, G. W. & Grey, W. G. 2008 Essentials of Multiphase Flow in Porous Media. Wiley.Google Scholar
Preuss, K. 2008 Leakage of CO2 from geologic storage: role of secondary accumulation at shallow depth. Intl J. Greenh. Gas Control 2, 37–46.Google Scholar
Pritchard, D. 2007 Gravity currents over fractured substrates in a porous medium. J. Fluid Mech. 584, 415–431.Google Scholar
Woods, A. W. 2015 Flow in Porous Rocks. Cambridge University Press.Google Scholar
Woods, A. W. & Fitzgerald, S. D. 1993 The vapourization of liquid moving through hot porous rock. J. Fluid Mech. 251, 563–579.Google Scholar