Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-12-01T02:19:44.307Z Has data issue: false hasContentIssue false
  • English
  • Français

Compressible Taylor–Couette flow – instability mechanism and codimension 3 points

Published online by Cambridge University Press:  10 June 2014

Stephanie Welsh ,
Evy Kersalé  and
Chris A. Jones
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Taylor–Couette flow in a compressible perfect gas is studied. The onset of instability is examined as a function of the Reynolds numbers of the inner and outer cylinder, the Mach number of the flow and the Prandtl number of the gas. We focus on the case of a wide gap, with radius ratio 0.5. We find new modes of instability at high Prandtl number, which can allow oscillatory axisymmetric modes to onset first. We also find that onset can occur even when the angular momentum increases outwards, so that the classical Rayleigh criterion can be violated in the compressible case. We have also considered the case of counter-rotating cylinders, where the 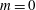$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}m=0$ and 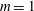$m=1$ modes can onset simultaneously to give a codimension 2 bifurcation, leading to the formation of complex flow patterns. In compressible flow we also find codimension 3 points. The Mach number and the critical inner and outer Reynolds numbers can be adjusted so that the two neutral curves for the 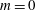$m=0$ and 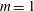$m=1$ modes touch rather than cross. Complex codimension 3 points occur more readily in the compressible case than in the Boussinesq case, and they are expected to lead to a rich nonlinear behaviour.

JFM classification

Nonlinear Dynamical Systems: Bifurcation Compressible Flows: Gas dynamics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 750 , 10 July 2014 , pp. 555 - 577
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/3.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© 2014 Cambridge University Press

References

Armitage, P. J. 2011 Dynamics of Protoplanetary Disks. Annu. Rev. Astron. Astrophys. 49, 195–236.CrossRefGoogle Scholar
Balbus, S. A. & Hawley, J. F. 1998 Instability, turbulence, and enhanced transport in accretion disks. Rev. Mod. Phys. 70, 1–53.CrossRefGoogle Scholar
Chandrasekhar, S. 1961 Hydrodynamic and Hydromagnetic Stability. Oxford University Press.Google Scholar
Chossat, P. & Iooss, G. 1994 The Taylor–Couette Problem, Applied Mathematical Sciences, vol. 102. Springer.CrossRefGoogle Scholar
Davey, A., DiPrima, R. C. & Stuart, J. T. 1968 On the instability of Taylor vortices. J. Fluid Mech. 31, 17–62.CrossRefGoogle Scholar
DiPrima, R. C., Eagles, P. M. & Ng, B. S. 1984 The effect of radius ratio on the stability of Couette flow and Taylor vortex flow. Phys. Fluids 27, 2403–2411.Google Scholar
Dubrulle, B., Dauchot, O., Daviaud, F., Longaretti, P.-Y., Richard, D. & Zahn, J.-P. 2005 Stability and turbulent transport in Taylor–Couette flow from analysis of experimental data. Phys. Fluids 17 (9), 095103.Google Scholar
Goodman, J. & Ji, H. 2002 Magnetorotational instability of dissipative Couette flow. J. Fluid Mech. 462, 365–382.Google Scholar
Hatay, F. F., Biringen, S., Erlebacher, G. & Zorumski, W. E. 1993 Stability of high-speed compressible rotating Couette flow. Phys. Fluids 5, 393–404.Google Scholar
Hersant, F., Dubrulle, B. & Huré, J.-M. 2005 Turbulence in circumstellar disks. Astron. Astrophys. 429, 531–542.Google Scholar
Ji, H., Burin, M., Schartman, E. & Goodman, J. 2006 Hydrodynamic turbulence cannot transport angular momentum effectively in astrophysical disks. Nature 444, 343–346.CrossRefGoogle ScholarPubMed
Kao, K.-H. & Chow, C.-Y. 1992 Linear stability of compressible Taylor–Couette flow. Phys. Fluids 4, 984–996.Google Scholar
Larignon, B. D., Marr, K. & Goldstein, D. B. 2006 Monte Carlo and Navier–Stokes simulations of compressible Taylor–Couette flow. J. Thermophys. Heat Transfer 20, 544–551.Google Scholar
Manela, A. & Frankel, I. 2007 On the compressible Taylor–Couette problem. J. Fluid Mech. 588, 59–74.Google Scholar
Paoletti, M. S. & Lathrop, D. P. 2011 Angular momentum transport in turbulent flow between independently rotating cylinders. Phys. Rev. Lett. 106 (2), 024501.Google Scholar
Paoletti, M. S., van Gils, D. P. M., Dubrulle, B., Sun, C., Lohse, D. & Lathrop, D. P. 2012 Angular momentum transport and turbulence in laboratory models of Keplerian flows. Astron. Astrophys. 547, A64.Google Scholar
Rogers, E. H. & Beard, D. W. 1969 A Numerical study of wide-gap Taylor vortices. J. Comput. Phys. 4, 1.Google Scholar
Schartman, E., Ji, H., Burin, M. J. & Goodman, J. 2012 Stability of quasi-Keplerian shear flow in a laboratory experiment. Astron. Astrophys. 543, A94.CrossRefGoogle Scholar
Signoret, F.1988 Étude de situations singulières et forçage périodique dans le problème de Couette–Taylor. PhD thesis, Université de Nice.Google Scholar
Signoret, F. & Iooss, G. 1988 Une singularité de codimension 3 dans le problème de Couette–Taylor. J. Méc. Théor. Appl. 7 (5), 545–572.Google Scholar
Stefani, F., Gundrum, T., Gerbeth, G., Rüdiger, G., Schultz, M., Szklarski, J. & Hollerbach, R. 2006 Experimental evidence for magnetorotational instability in a Taylor–Couette flow under the influence of a helical magnetic field. Phys. Rev. Lett. 97 (18), 184502.Google Scholar
Taylor, G. I. 1923 Stability of a viscous liquid contained between two rotating cylinders. Phil. Trans. R. Soc. Lond. A 223, 289–343.Google Scholar
Yih, C.-S. 1972 Spectral theory of Taylor vortices part II. Proof of nonoscillation. Arch. Rat. Mech. Anal. 47, 288–300.Google Scholar
Yoshida, H. & Aoki, K. 2006 Linear stability of the cylindrical Couette flow of a rarefied gas. Phys. Rev. E 73 (2), 021201.Google Scholar