Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-12-01T04:01:54.479Z Has data issue: false hasContentIssue false
  • English
  • Français

Compressibility regularizes the 𝜇(I)-rheology for dense granular flows

Published online by Cambridge University Press:  03 October 2017

J. Heyman Open the ORCID record for J. Heyman [Opens in a new window] ,
R. Delannay ,
H. Tabuteau  and
A. Valance
J. Heyman*
Affiliation:
Institut de Physique de Rennes, UMR CNRS 6251, Universit de Rennes 1, Campus de Beaulieu, Btiment 11A, 263 Avenue Gnral Leclerc, 35042 Rennes CEDEX, France
R. Delannay
Affiliation:
Institut de Physique de Rennes, UMR CNRS 6251, Universit de Rennes 1, Campus de Beaulieu, Btiment 11A, 263 Avenue Gnral Leclerc, 35042 Rennes CEDEX, France
H. Tabuteau
Affiliation:
Institut de Physique de Rennes, UMR CNRS 6251, Universit de Rennes 1, Campus de Beaulieu, Btiment 11A, 263 Avenue Gnral Leclerc, 35042 Rennes CEDEX, France
A. Valance
Affiliation:
Institut de Physique de Rennes, UMR CNRS 6251, Universit de Rennes 1, Campus de Beaulieu, Btiment 11A, 263 Avenue Gnral Leclerc, 35042 Rennes CEDEX, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

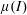The $\unicode[STIX]{x1D707}(I)$-rheology was recently proposed as a potential candidate to model the incompressible flow of frictional grains in the dense inertial regime. However, this rheology was shown to be ill-posed in the mathematical sense for a large range of parameters, notably in the low and large inertial number limits (Barker et al., J. Fluid Mech., vol. 779, 2015, pp. 794–818). In this rapid communication, we extend the stability analysis of Barker et al. (J. Fluid Mech., vol. 779, 2015, pp. 794–818) to compressible flows. We show that compressibility regularizes the equations, making the problem well-posed for all parameters, with the condition that sufficient dissipation be associated with volume changes. In addition to the usual Coulomb shear friction coefficient 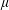$\unicode[STIX]{x1D707}$, we introduce a bulk friction coefficient 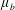$\unicode[STIX]{x1D707}_{b}$, associated with volume changes and show that the problem is well-posed if 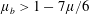$\unicode[STIX]{x1D707}_{b}>1-7\unicode[STIX]{x1D707}/6$. Moreover, we show that the ill-posed domain defined by Barker et al. (J. Fluid Mech., vol. 779, 2015, pp. 794–818) transforms into a domain where the flow is unstable but remains well-posed when compressibility is taken into account. These results suggest the importance of taking into account dynamic compressibility for the modelling of dense granular flows and open new perspectives to investigate the emission and propagation of acoustic waves inside these flows.

JFM classification

Acoustics: Acoustics Complex Fluids: Complex Fluids Granular media: Granular media
Type
Papers
Information
Journal of Fluid Mechanics , Volume 830 , 10 November 2017 , pp. 553 - 568
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alam, M. & Nott, P. R. 1997 The influence of friction on the stability of unbounded granular shear flow. J. Fluid Mech. 343, 267–301.CrossRefGoogle Scholar
Barker, T., Schaeffer, D. G., Bohorquez, P. & Gray, J. M. N. T. 2015 Well-posed and ill-posed behaviour of the 𝜇(I)-rheology for granular flow. J. Fluid Mech. 779, 794–818.Google Scholar
Barker, T., Schaeffer, D. G., Shearer, M. & Gray, J. M. N. T. 2017 Well-posed continuum equations for granular flow with compressibility and 𝜇(I)-rheology. Proc. R. Soc. Lond. A 473, 20160846.Google Scholar
Birkhoff, G. 1954 Classification of partial differential equations. J. Soc. Ind. Appl. Maths 2 (1), 57–67.CrossRefGoogle Scholar
Börzsönyi, T., Ecke, R. E. & McElwaine, J. N. 2009 Patterns in flowing sand: understanding the physics of granular flow. Phys. Rev. Lett. 103, 178302.Google Scholar
Bouchut, F., Fernandez-Nieto, E. D., Mangeney, A. & Narbona-Reina, G. 2016 A two-phase two-layer model for fluidized granular flows with dilatancy effects. J. Fluid Mech. 801, 166–221.CrossRefGoogle Scholar
Brodu, N., Delannay, R., Valance, A. & Richard, P. 2015 New patterns in high-speed granular flows. J. Fluid Mech. 769, 218–228.Google Scholar
Brodu, N., Richard, P. & Delannay, R. 2013 Shallow granular flows down flat frictional channels: steady flows and longitudinal vortices. Phys. Rev. E 87, 022202.Google ScholarPubMed
da Cruz, F., Emam, S., Prochnow, M., Roux, J.-N. & Chevoir, F. 2005 Rheophysics of dense granular materials: discrete simulation of plane shear flows. Phys. Rev. E 72, 021309.Google ScholarPubMed
Forterre, Y. & Pouliquen, O. 2002 Stability analysis of rapid granular chute flows: formation of longitudinal vortices. J. Fluid Mech. 467, 361–387.Google Scholar
GDR MiDi 2004 On dense granular flows. Eur. Phys. J. E 14 (4), 341–365.Google Scholar
Goddard, J. D. 2014 Continuum modeling of granular media. Appl. Mech. Rev. 66 (5), 050801.CrossRefGoogle Scholar
Hadamard, J. 1922 Lectures on Cauchy’s Problem. Yale University Press.Google Scholar
Jackson, R. 1983 Some mathematical and physical aspects of continuum models for the motion of granular materials. In Theory of Dispersed Multiphase Flow (ed. Meyer, R.), pp. 291–336. Academic.Google Scholar
Jop, P., Forterre, Y. & Pouliquen, O. 2006 A constitutive law for dense granular flows. Nature 441 (7094), 727–730.Google Scholar
Joseph, D. D. & Saut, J. C. 1990 Short-wave instabilities and ill-posed initial-value problems. Theor. Comput. Fluid Dyn. 1 (4), 191–227.Google Scholar
Kamrin, K. & Koval, G. 2012 Nonlocal constitutive relation for steady granular flow. Phys. Rev. Lett. 108, 178301.Google Scholar
Khorrami, M. R. 1991 A Chebyshev spectral collocation method using a staggered grid for the stability of cylindrical flows. Intl J. Numer. Meth. Fluids 12 (9), 825–833.CrossRefGoogle Scholar
Krishnaraj, K. P. & Nott, P. R. 2016 A dilation-driven vortex flow in sheared granular materials explains a rheometric anomaly. Nat. Commun. 7, 10630.CrossRefGoogle ScholarPubMed
Melosh, H. J. 1979 Acoustic fluidization: a new geologic process? J. Geophys. Res. 84 (B13), 7513–7520.Google Scholar
Muite, B. K., Quinn, S. F., Sundaresan, S. & Rao, K. K. 2004 Silo music and silo quake: granular flow-induced vibration. Powder Technol. 145 (3), 190–202.Google Scholar
Nott, P. R. 2009 Classical and cosserat plasticity and viscoplasticity models for slow granular flow. Acta Mechanica 205 (1), 151–160.Google Scholar
Paihla, M. & Pouliquen, O. 2009 A two-phase flow description of the initiation of underwater granular avalanches. J. Fluid Mech. 633, 115–135.Google Scholar
Pitman, E. B. & Schaeffer, D. G. 1987 Stability of time dependent compressible granular flow in two dimensions. Commun. Pure Appl. Maths 40 (4), 421–447.Google Scholar
Prakash, J. R. & Rao, K. K. 1988 Steady compressible flow of granular materials through a wedge-shaped hopper: the smooth wall, radial gravity problem. Chem. Engng Sci. 43 (3), 479–494.Google Scholar
Roux, S. & Radjai, F. 1998 Texture-dependent rigid-plastic behavior. Appl. Sci. Phys. Dry Granular Media E 350, 229–236.CrossRefGoogle Scholar
Schaeffer, D. G. 1987 Instability in the evolution equations describing incompressible granular flow. J. Differ. Equ. 66 (1), 19–50.Google Scholar
Trulsson, M., Bouzid, M., Claudin, P. & Andreotti, B. 2013 Dynamic compressibility of dense granular shear flows. Europhys. Lett. 103, 38002.CrossRefGoogle Scholar