Article contents
Complex singularity analysis for vortex layer flows
Published online by Cambridge University Press: 03 December 2021
Abstract
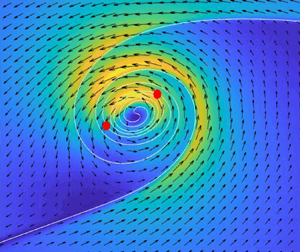
We study the evolution of a 2D vortex layer at high Reynolds number. Vortex layer flows are characterized by intense vorticity concentrated around a curve. In addition to their intrinsic interest, vortex layers are relevant configurations because they are regularizations of vortex sheets. In this paper, we consider vortex layers whose thickness is proportional to the square-root of the viscosity. We investigate the typical roll-up process, showing that crucial phases in the initial flow evolution are the formation of stagnation points and recirculation regions. Stretching and folding characterizes the following stage of the dynamics, and we relate these events to the growth of the palinstrophy. The formation of an inner vorticity core, with vorticity intensity growing to infinity for larger Reynolds number, is the final phase of the dynamics. We display the inner core's self-similar structure, with the scale factor depending on the Reynolds number. We reveal the presence of complex singularities in the solutions of Navier–Stokes equations; these singularities approach the real axis with increasing Reynolds number. The comparison between these singularities and the Birkhoff–Rott singularity seems to suggest that vortex layers, in the limit  $Re\rightarrow \infty$, behave differently from vortex sheets.
$Re\rightarrow \infty$, behave differently from vortex sheets.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
REFERENCES
- 5
- Cited by



