Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-23T05:08:59.676Z Has data issue: false hasContentIssue false
  • English
  • Français

Complete self-preservation on the axis of a turbulent round jet

Published online by Cambridge University Press:  01 February 2016

L. Djenidi ,
R. A. Antonia ,
N. Lefeuvre  and
J. Lemay Open the ORCID record for J. Lemay [Opens in a new window]
L. Djenidi*
Affiliation:
Discipline of Mechanical Engineering, School of Engineering, University of Newcastle, Newcastle, 2308 NSW, Australia
R. A. Antonia
Affiliation:
Discipline of Mechanical Engineering, School of Engineering, University of Newcastle, Newcastle, 2308 NSW, Australia
N. Lefeuvre
Affiliation:
Discipline of Mechanical Engineering, School of Engineering, University of Newcastle, Newcastle, 2308 NSW, Australia
J. Lemay
Affiliation:
Department of mechanical Engineering, University Laval, Quebec City, GVI 0A6, Canada
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Self-preservation (SP) solutions on the axis of a turbulent round jet are derived for the transport equation of the second-order structure function of the turbulent kinetic energy (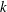$k$), which may be interpreted as a scale-by-scale (s.b.s.) energy budget. The analysis shows that the mean turbulent energy dissipation rate, $\overline{{\it\epsilon}}$, evolves like 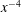$x^{-4}$ ($x$ is the streamwise direction). It is important to stress that this derivation does not use the constancy of the non-dimensional dissipation rate parameter 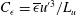$C_{{\it\epsilon}}=\overline{{\it\epsilon}}u^{\prime 3}/L_{u}$ (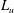$L_{u}$ and 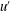$u^{\prime }$ are the integral length scale and root mean square of the longitudinal velocity fluctuation respectively). We show, in fact, that the constancy of 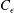$C_{{\it\epsilon}}$ is simply a consequence of complete SP (i.e. SP at all scales of motion). The significance of the analysis relates to the fact that the SP requirements for the mean velocity and mean turbulent kinetic energy (i.e. 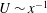$U\sim x^{-1}$ and 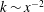$k\sim x^{-2}$ respectively) are derived without invoking the transport equations for 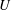$U$ and 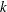$k$. Experimental hot-wire data along the axis of a turbulent round jet show that, after a transient downstream distance which increases with Reynolds number, the turbulence statistics comply with complete SP. For example, the measured $\overline{{\it\epsilon}}$ agrees well with the SP prediction, i.e. 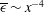$\overline{{\it\epsilon}}\sim x^{-4}$, while the Taylor microscale Reynolds number 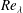$Re_{{\it\lambda}}$ remains constant. The analytical expression for the prefactor 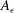$A_{{\it\epsilon}}$ for 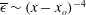$\overline{{\it\epsilon}}\sim (x-x_{o})^{-4}$ (where 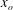$x_{o}$ is a virtual origin), first developed by Thiesset et al. (J. Fluid Mech., vol. 748, 2014, R2) and rederived here solely from the SP analysis of the s.b.s. energy budget, is validated and provides a relatively simple and accurate method for estimating $\overline{{\it\epsilon}}$ along the axis of a turbulent round jet.

JFM classification

Wakes/Jets: Jets Turbulent Flows: Turbulence theory Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 790 , 10 March 2016 , pp. 57 - 70
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Antonia, R. A. & Mi, J. 1993 Temperature dissipation in a turbulent round jet. J. Fluid Mech. 250, 531–551.CrossRefGoogle Scholar
Antonia, R. A., Satyaprakash, B. R. & Hussain, A. K. M. F. 1980 Measurements of dissipation rate and some other characteristics of turbulent plane and circular jets. Phys. Fluids 23 (4), 695–700.CrossRefGoogle Scholar
Antonia, R. A., Zhou, T. & Zhu, Y. 1998 Three-component vorticity measurements in a turbulent grid flow. J. Fluid Mech. 374, 29–57.Google Scholar
Burattini, P., Antonia, R. A. & Danaila, L. 2005a Scale-by-scale energy budget on the axis of a turbulent round jet. J. Turbul. 6, 1–11.Google Scholar
Burattini, P., Antonia, R. A. & Danaila, L. 2005b Similarity in the far field of a turbulent round jet. Phys. Fluids 17, 025101–025115.CrossRefGoogle Scholar
Danaila, L., Antonia, R. A. & Burattini, P. 2004 Progress in studying small-scale turbulence using ‘exact’ two-point equations. New J. Phys. 6, 128.CrossRefGoogle Scholar
Darisse, A., Lemay, J. & Benaissa, A. 2014 Extensive study of temperature dissipation measurements on the centreline of turbulent round jet based on the ${\it\theta}^{2}/2$ budget. Exp. Fluids 55:1623, 1–15.Google Scholar
Darisse, A., Lemay, J. & Benaissa, A. 2015 Budgets of turbulent kinetic energy, Reynolds stresses, variance of temperature fluctuations and turbulent heat fluxes in a round jet. J. Fluid Mech. 774, 95–142.CrossRefGoogle Scholar
Djenidi, L. & Antonia, R. A. 2015 A general self-preservation analysis for decaying homogeneous isotropic turbulence. J. Fluid Mech. 773, 345–365.Google Scholar
Ewing, D., Frohnapfel, B., George, W. K., Pedersen, J. M. & Westerweel, J. 2007 Two-point similarity in the round jet. J. Fluid Mech. 577, 309–330.CrossRefGoogle Scholar
Friehe, C. A., Atta, C. W. & Van Gibson, C. H. 1971 Jet turbulence: dissipation rate measurements and correlations. AGARD Turbul. Shear Flows 18, 1–7.Google Scholar
George, W. K. 2012 Asymptotic effect on initial and upstream conditions on turbulence. Trans. ASME J. Fluids Engng 134, 061203.Google Scholar
Gouldin, F. C., Schefer, R. W., Johnson, S. C. & Kollman, W. 1986 Nonreacting turbulent mixing flows. Prog. Energy Combust. Sci. 12, 257–303.CrossRefGoogle Scholar
Hussein, H. J., Capp, S. P. & George, W. K. 1994 Velocity measurements in a high-Reynolds-number, momentum-conserving, axisymmetric, turbulent jet. J. Fluid Mech. 258, 31–75.CrossRefGoogle Scholar
Kahalerras, H., Malecot, Y., Gagne, Y. & Castaing, B. 1998 Intermittency and Reynolds number. Phys. Fluids 10 (4), 075101.CrossRefGoogle Scholar
Lumley, J. L. 1978 Computational modelling of turbulent flows. Adv. Appl. Mech. 18, 123–176.CrossRefGoogle Scholar
Mi, J., Xu, M. & Zhou, T. 2013 Reynolds number influence on statistical behaviors of turbulence in a circular free jet. Phys. Fluids 25, 075101.Google Scholar
Panchapakesan, N. R. & Lumley, J. L. 1993 Turbulence measurements in axisymmetric jets of air and helium. Part 1. Air jet. J. Fluid Mech. 246, 197–223.CrossRefGoogle Scholar
Sadeghi, H., Lavoie, P. & Pollard, A. 2015 Equilibrium similarity solution of the turbulent transport equation along the centreline of a round jet. J. Fluid Mech. 772, 740–755.Google Scholar
Taub, G. N., Lee, H., Balachandar, S. & Sherif, S. A. 2013 A direct numerical simulation study of higher order statistics in a turbulent round jet. Phys. Fluids 25, 115102.CrossRefGoogle Scholar
Thiesset, F., Antonia, R. A. & Djenidi, L. 2014 Consequences of self-preservation on the axis of a turbulent round jet. J. Fluid Mech. 748, R2.Google Scholar