Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-12-01T01:41:51.107Z Has data issue: false hasContentIssue false
  • English
  • Français

Competition between the centrifugal and strato-rotational instabilities in the stratified Taylor–Couette flow

Published online by Cambridge University Press:  06 February 2018

Junho Park Open the ORCID record for Junho Park [Opens in a new window] ,
Paul Billant ,
Jong-Jin Baik  and
Jaemyeong Mango Seo
Junho Park*
Affiliation:
School of Earth and Environmental Sciences, Seoul National University, Seoul 08826, Republic of Korea
Paul Billant
Affiliation:
LadHyX, CNRS, Ecole Polytechnique, F-91128 Palaiseau CEDEX, France
Jong-Jin Baik
Affiliation:
School of Earth and Environmental Sciences, Seoul National University, Seoul 08826, Republic of Korea
Jaemyeong Mango Seo
Affiliation:
School of Earth and Environmental Sciences, Seoul National University, Seoul 08826, Republic of Korea
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The stably stratified Taylor–Couette flow is investigated experimentally and numerically through linear stability analysis. In the experiments, the stability threshold and flow regimes have been mapped over the ranges of outer and inner Reynolds numbers: 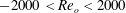$-2000<Re_{o}<2000$ and 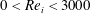$0<Re_{i}<3000$, for the radius ratio 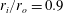$r_{i}/r_{o}=0.9$ and the Brunt–Väisälä frequency 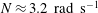$N\approx 3.2~\text{rad}~\text{s}^{-1}$. The corresponding Froude numbers 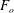$F_{o}$ and 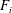$F_{i}$ are always much smaller than unity. Depending on 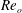$Re_{o}$ (or equivalently on the angular velocity ratio 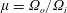$\unicode[STIX]{x1D707}=\unicode[STIX]{x1D6FA}_{o}/\unicode[STIX]{x1D6FA}_{i}$), three different regimes have been identified above instability onset: a weakly non-axisymmetric mode with low azimuthal wavenumber 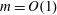$m=O(1)$ is observed for 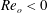$Re_{o}<0$ (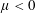$\unicode[STIX]{x1D707}<0$), a highly non-axisymmetric mode with 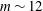$m\sim 12$ occurs for 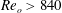$Re_{o}>840$ (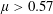$\unicode[STIX]{x1D707}>0.57$) while both modes are present simultaneously in the lower and upper parts of the flow for 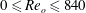$0\leqslant Re_{o}\leqslant 840$ (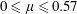$0\leqslant \unicode[STIX]{x1D707}\leqslant 0.57$). The destabilization of these primary modes and the transition to turbulence as 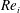$Re_{i}$ increases have been also studied. The linear stability analysis proves that the weakly non-axisymmetric mode is due to the centrifugal instability while the highly non-axisymmetric mode comes from the strato-rotational instability. These two instabilities can be clearly distinguished because of their distinct dominant azimuthal wavenumber and frequency, in agreement with the recent results of Park et al. (J. Fluid Mech., vol. 822, 2017, pp. 80–108). The stability threshold and the characteristics of the primary modes observed in the experiments are in very good agreement with the numerical predictions. Moreover, we show that the centrifugal and strato-rotational instabilities are observed simultaneously for 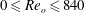$0\leqslant Re_{o}\leqslant 840$ in the lower and upper parts of the flow, respectively, because of the variations of the local Reynolds numbers along the vertical due to the salinity gradient.

JFM classification

Instability: Instability Geophysical and Geological Flows: Stratified flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 840 , 10 April 2018 , pp. 5 - 24
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andereck, C. D., Liu, S. S. & Swinney, H. L. 1986 Flow regimes in a circular Couette system with independently rotating cylinders. J. Fluid Mech. 164, 155–183.CrossRefGoogle Scholar
Antkowiak, A.2005 Dynamique aux temps courts d’un tourbillon isolé. PhD thesis, Université Paul Sabatier de Toulouse.Google Scholar
Boubnov, B. M., Gledzer, E. B. & Hopfinger, E. J. 1995 Stratified circular Couette flow: instability and flow regimes. J. Fluid Mech. 292, 333–358.CrossRefGoogle Scholar
Dubrulle, B., Dauchot, O., Daviaud, F., Longaretti, P.-Y., Richard, D. & Zahn, J.-P. 2005a Stability and turbulent transport in Taylor–Couette flow from analysis of experimental data. Phys. Fluids 17, 095103.CrossRefGoogle Scholar
Dubrulle, B., Marié, L., Normand, C., Richard, D., Hersant, F. & Zahn, J.-P. 2005b An hydrodynamic shear instability in stratified disks. Astron. Astrophys. 29, 1–13.CrossRefGoogle Scholar
Ibanez, R., Swinney, H. L. & Rodenborn, B. 2016 Observations of the stratorotational instability in rotating concentric cylinders. Phys. Rev. Fluids 1, 053601.Google Scholar
Le Bars, M. & Le Gal, P. 2007 Experimental analysis of the stratorotational instability in a cylindrical Couette flow. Phys. Rev. Lett. 99, 064502.Google Scholar
Leclercq, C., Nguyen, F. & Kerswell, R. R. 2016a Connections between centrifugal, stratorotational, and radiative instabilities in viscous Taylor–Couette flow. Phys. Rev. E 94, 043103.Google Scholar
Leclercq, C., Partridge, J. L., Augier, P., Caulfield, C. P., Dalziel, S. B. & Linden, P. F.2016b Nonlinear waves in stratified Taylor-Couette flow. Part 1. Layer formation. arXiv:1609.02885.Google Scholar
Molemaker, M. J., McWilliams, J. C. & Yavneh, I. 2001 Instability and equilibration of centrifugally stable stratified Taylor–Couette flow. Phys. Rev. Lett. 86, 5270–5273.Google Scholar
Oster, G. 1965 Density gradients. Sci. Am. 213, 70–76.CrossRefGoogle Scholar
Park, J.2012 Waves and instabilities on vortices in stratified and rotating fluids. PhD thesis, Ecole Polytechnique.Google Scholar
Park, J. & Billant, P. 2013 The stably stratified Taylor–Couette flow is always unstable except for solid-body rotation. J. Fluid Mech. 725, 262–280.Google Scholar
Park, J., Billant, P. & Baik, J.-J. 2017 Instabilities and transient growth of the stratified Taylor–Couette flow in a Rayleigh-unstable regime. J. Fluid Mech. 822, 80–108.Google Scholar
Shalybkov, D. & Rüdiger, G. 2005 Stability of density-stratified viscous Taylor–Couette flows. Astron. Astrophys. 438, 411–417.Google Scholar
Tagg, R., Edwards, W. S., Swinney, H. L. & Marcus, P. S. 1989 Nonlinear standing waves in Couette–Taylor flow. Phys. Rev. A 39, 3734.CrossRefGoogle ScholarPubMed
Taylor, G. I. 1923 Stability of a viscous liquid contained between two rotating cylinders. Phil. R. Soc. Lond. A 223, 289–343.Google Scholar
Withjack, E. M. & Chen, C. F. 1974 An experimental study of Couette instability of stratified fluids. J. Fluid Mech. 66, 725–737.Google Scholar
Yavneh, I., McWilliams, J. C. & Molemaker, M. J. 2001 Non-axisymmetric instability of centrifugally stable stratified Taylor–Couette flow. J. Fluid Mech. 448, 1–21.Google Scholar