Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-28T17:45:24.891Z Has data issue: false hasContentIssue false
  • English
  • Français

Comparison of turbulent boundary layers over smooth and rough surfaces up to high Reynolds numbers

Published online by Cambridge University Press:  14 April 2016

D. T. Squire ,
C. Morrill-Winter ,
N. Hutchins ,
M. P. Schultz ,
J. C. Klewicki  and
I. Marusic
D. T. Squire*
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Melbourne, VIC 3010, Australia
C. Morrill-Winter
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Melbourne, VIC 3010, Australia
N. Hutchins
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Melbourne, VIC 3010, Australia
M. P. Schultz
Affiliation:
Department of Naval Architecture and Ocean Engineering, US Naval Academy, Annapolis, MD 21402, USA
J. C. Klewicki
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Melbourne, VIC 3010, Australia Mechanical Engineering Department, University of New Hampshire, Durham, NH 03824, USA
I. Marusic
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Melbourne, VIC 3010, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

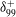Turbulent boundary layer measurements above a smooth wall and sandpaper roughness are presented across a wide range of friction Reynolds numbers, ${\it\delta}_{99}^{+}$, and equivalent sand grain roughness Reynolds numbers, 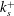$k_{s}^{+}$ (smooth wall: 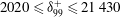$2020\leqslant {\it\delta}_{99}^{+}\leqslant 21\,430$, rough wall: 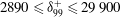$2890\leqslant {\it\delta}_{99}^{+}\leqslant 29\,900$; 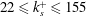$22\leqslant k_{s}^{+}\leqslant 155$; and 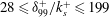$28\leqslant {\it\delta}_{99}^{+}/k_{s}^{+}\leqslant 199$). For the rough-wall measurements, the mean wall shear stress is determined using a floating element drag balance. All smooth- and rough-wall data exhibit, over an inertial sublayer, regions of logarithmic dependence in the mean velocity and streamwise velocity variance. These logarithmic slopes are apparently the same between smooth and rough walls, indicating similar dynamics are present in this region. The streamwise mean velocity defect and skewness profiles each show convincing collapse in the outer region of the flow, suggesting that Townsend’s (The Structure of Turbulent Shear Flow, vol. 1, 1956, Cambridge University Press.) wall-similarity hypothesis is a good approximation for these statistics even at these finite friction Reynolds numbers. Outer-layer collapse is also observed in the rough-wall streamwise velocity variance, but only for flows with 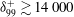${\it\delta}_{99}^{+}\gtrsim 14\,000$. At Reynolds numbers lower than this, profile invariance is only apparent when the flow is fully rough. In transitionally rough flows at low 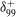${\it\delta}_{99}^{+}$, the outer region of the inner-normalised streamwise velocity variance indicates a dependence on 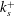$k_{s}^{+}$ for the present rough surface.

JFM classification

Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 795 , 25 May 2016 , pp. 210 - 240
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abe, H., Kawamura, H. & Choi, H. 2004 Very large-scale structures and their effects on the wall shear-stress fluctuations in a turbulent channel flow up to Re 𝜏 = 640. Trans. ASME J. Fluids Engng 126 (5), 835–843.CrossRefGoogle Scholar
Acharya, M., Bornstein, J. & Escudier, M. P. 1986 Turbulent boundary layers on rough surfaces. Exp. Fluids 4 (1), 33–47.CrossRefGoogle Scholar
Afzal, N. 1982 Fully developed turbulent flow in a pipe: an intermediate layer. Ing.-Arch. 52 (6), 355–377.Google Scholar
Akinlade, O. G., Bergstrom, D. J., Tachie, M. F. & Castillo, L. 2004 Outer flow scaling of smooth and rough wall turbulent boundary layers. Exp. Fluids 37, 604–612.CrossRefGoogle Scholar
Allen, J. J., Shockling, M. A., Kunkel, G. J. & Smits, A. J. 2007 Turbulent flow in smooth and rough pipes. Phil. Trans. R. Soc. Lond. A 365 (1852), 699–714.Google Scholar
Baars, W. J., Squire, D. T., Talluru, K. M., Abbassi, M. R., Hutchins, N. & Marusic, I.2016 Wall-drag measurements of smooth- and rough-wall turbulent boundary layers using a floating element. Exp. Fluids (under review).Google Scholar
Bergstrom, D. J., Akinlade, O. G. & Tachie, M. F. 2005 Skin friction correlation for smooth and rough wall turbulent boundary layers. Trans. ASME J. Fluids Engng 127 (6), 1146–1153.Google Scholar
Bhaganagar, K., Kim, J. & Coleman, G. 2004 Effect of roughness on wall-bounded turbulence. Flow Turbul. Combust. 72 (2–4), 463–492.CrossRefGoogle Scholar
Brzek, B., Cal, R. B., Johansson, G. & Castillo, L. 2007 Inner and outer scalings in rough surface zero pressure gradient turbulent boundary layers. Phys. Fluids 19 (6), 065101.Google Scholar
Castro, I. P. 2007 Rough-wall boundary layers: mean flow universality. J. Fluid Mech. 585, 469–485.CrossRefGoogle Scholar
Castro, I. P., Segalini, A. & Alfredsson, P. H. 2013 Outer-layer turbulence intensities in smooth- and rough-wall boundary layers. J. Fluid Mech. 727, 119–131.CrossRefGoogle Scholar
Chan, L., MacDonald, M., Chung, D., Hutchins, N. & Ooi, A. 2015 A systematic investigation of roughness height and wavelength in turbulent pipe flow in the transitionally rough regime. J. Fluid Mech. 771, 743–777.Google Scholar
Chauhan, K. A., Monkewitz, P. A. & Nagib, H. M. 2009 Criteria for assessing experiments in zero pressure gradient boundary layers. Fluid Dyn. Res. 41 (2), 021404.Google Scholar
Chin, C., Philip, J., Klewicki, J. C., Ooi, A. & Marusic, I. 2014 Reynolds-number-dependent turbulent inertia and onset of log region in pipe flows. J. Fluid Mech. 757, 747–769.Google Scholar
Clauser, F. H. 1956 The turbulent boundary layer. Adv. Appl. Mech. 4, 1–51.CrossRefGoogle Scholar
Coles, D. E.1962 A manual of experimental boundary-layer practice for low-speed flow. RAND Corp. Rep. R-403-PR. The Rand Corp, Santa Monica, CA, USA.Google Scholar
De Graaff, D. B. & Eaton, J. K. 2000 Reynolds-number scaling of the flat-plate turbulent boundary layer. J. Fluid Mech. 422, 319–346.Google Scholar
Efros, V. & Krogstad, P.-Å. 2011 Development of a turbulent boundary layer after a step from smooth to rough surface. Exp. Fluids 51 (6), 1563–1575.Google Scholar
Erm, L. P. & Joubert, P. N. 1991 Low-Reynolds-number turbulent boundary layers. J. Fluid Mech. 230, 1–44.CrossRefGoogle Scholar
Flack, K. A., Schultz, M. P. & Connelly, J. S. 2007 Examination of a critical roughness height for outer layer similarity. Phys. Fluids 19 (9), 095104.Google Scholar
Flack, K. A., Schultz, M. P. & Shapiro, T. A. 2005 Experimental support for Townsend‘s Reynolds number similarity hypothesis on rough walls. Phys. Fluids 17 (3), 035102.CrossRefGoogle Scholar
Flores, O. & Jimenez, J. 2006 Effect of wall-boundary disturbances on turbulent channel flows. J. Fluid Mech. 566, 357–376.Google Scholar
Foss, J. & Haw, R. 1990 Transverse vorticity measurements using a compact array of four sensors. T. Heuris. Therm. Anemom. 97, 71–76.Google Scholar
Grass, A. J. 1971 Structural features of turbulent flow over smooth and rough boundaries. J. Fluid Mech. 50 (02), 233–255.Google Scholar
Harun, Z., Monty, J. P., Mathis, R. & Marusic, I. 2013 Pressure gradient effects on the large-scale structure of turbulent boundary layers. J. Fluid Mech. 715, 477–498.Google Scholar
Hong, J., Katz, J. & Schultz, M. P. 2011 Near-wall turbulence statistics and flow structures over three-dimensional roughness in a turbulent channel flow. J. Fluid Mech. 667, 1–37.CrossRefGoogle Scholar
Hultmark, M., Vallikivi, M., Bailey, S. C. C. & Smits, A. J. 2013 Logarithmic scaling of turbulence in smooth- and rough-wall pipe flow. J. Fluid Mech. 728, 376–395.Google Scholar
Hutchins, N. & Marusic, I. 2007a Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.Google Scholar
Hutchins, N. & Marusic, I. 2007b Large-scale influences in near-wall turbulence. Phil. Trans. R. Soc. Lond. A 365 (1852), 647–664.Google ScholarPubMed
Hutchins, N., Nickels, T. B., Marusic, I. & Chong, M. S. 2009 Hot-wire spatial resolution issues in wall-bounded turbulence. J. Fluid Mech. 635, 103.Google Scholar
Jackson, P. S. 1981 On the displacement height in the logarithmic velocity profile. J. Fluid Mech. 111, 15–25.Google Scholar
Jiménez, J. 2004 Turbulent flows over rough walls. Annu. Rev. Fluid Mech. 36, 173–196.CrossRefGoogle Scholar
Keirsbulck, L., Labraga, L., Mazouz, A. & Tournier, C. 2002 Surface roughness effects on turbulent boundary layer structures. Trans. ASME J. Fluids Engng 124 (1), 127–135.Google Scholar
Klewicki, J. C., Fife, P. & Wei, T. 2009 On the logarithmic mean profile. J. Fluid Mech. 638, 73–93.Google Scholar
Krogstad, P.-Å., Antonia, R. A. & Browne, L. W. B. 1992 Comparison between rough- and smooth-wall turbulent boundary layers. J. Fluid Mech. 245, 599–617.Google Scholar
Krogstad, P.-Å. & Efros, V. 2010 Rough wall skin friction measurements using a high resolution surface balance. Intl J. Heat Fluid Flow 31 (3), 429–433.Google Scholar
Krogstad, P.-Å. & Efros, V. 2012 About turbulence statistics in the outer part of a boundary layer developing over two-dimensional surface roughness. Phys. Fluids 24 (7), 075112.Google Scholar
Krogstadt, P.-Å. & Antonia, R. A. 1999 Surface roughness effects in turbulent boundary layers. Exp. Fluids 27 (5), 450–460.CrossRefGoogle Scholar
Lee, S.-H. & Sung, H. J. 2007 Direct numerical simulation of the turbulent boundary layer over a rod-roughened wall. J. Fluid Mech. 584, 125–146.CrossRefGoogle Scholar
Leonardi, S., Orlandi, P., Smalley, R. J., Djenidi, L. & Antonia, R. A. 2003 Direct numerical simulations of turbulent channel flow with transverse square bars on one wall. J. Fluid Mech. 491, 229–238.CrossRefGoogle Scholar
Ligrani, P. M. & Moffat, R. J. 1986 Structure of transitionally rough and fully rough turbulent boundary layers. J. Fluid Mech. 162, 69–98.CrossRefGoogle Scholar
Marusic, I., Chauhan, K. A., Kulandaivelu, V. & Hutchins, N. 2015 Evolution of zero-pressure-gradient boundary layers from different tripping conditions. J. Fluid Mech. 783, 379–411.Google Scholar
Marusic, I., Monty, J. P., Hultmark, M. & Smits, A. J. 2013 On the logarithmic region in wall turbulence. J. Fluid Mech. 716, R3.Google Scholar
Mehdi, F., Klewicki, J. C. & White, C. M. 2013 Mean force structure and its scaling in rough-wall turbulent boundary layers. J. Fluid Mech. 731, 682–712.Google Scholar
Monty, J. P., Allen, J. J., Lien, K. & Chong, M. S. 2011 Modification of the large-scale features of high Reynolds number wall turbulence by passive surface obtrusions. Exp. Fluids 51 (6), 1755–1763.Google Scholar
Morrill-Winter, C., Klewicki, J. C., Baidya, R. & Marusic, I. 2015 Temporally optimized spanwise vorticity sensor measurements in turbulent boundary layers. Exp. Fluids 56, 216.Google Scholar
Mulhearn, P. J. & Finnigan, J. J. 1978 Turbulent flow over a very rough, random surface. Boundary-Layer Meteorol. 15 (1), 109–132.Google Scholar
Nickels, T. B., Marusic, I., Hafez, S. & Chong, M. S. 2005 Evidence of the k-1 law in a high-Reynolds-number turbulent boundary layer. Phys. Rev. Lett. 95 (7), 074501.Google Scholar
Nickels, T. B., Marusic, I., Hafez, S., Hutchins, N. & Chong, M. S. 2007 Some predictions of the attached eddy model for a high Reynolds number boundary layer. Phil. Trans. R. Soc. Lond. A 365 (1852), 807–822.Google Scholar
Nikuradse, J.1933 Laws of flow in rough pipes. NASA Tech. Memo. 1292.Google Scholar
Perry, A. E. & Joubert, P. N. 1963 Rough-wall boundary layers in adverse pressure gradients. J. Fluid Mech. 17 (02), 193–211.Google Scholar
Perry, A. E. & Li, J. D. 1990 Experimental support for the attached-eddy hypothesis in zero-pressure-gradient turbulent boundary layers. J. Fluid Mech. 218, 405–438.Google Scholar
Perry, A. E., Marusic, I. & Jones, M. B. 2002 On the streamwise evolution of turbulent boundary layers in arbitrary pressure gradients. J. Fluid Mech. 461, 61–91.Google Scholar
Perry, A. E., Schofield, W. H. & Joubert, P. N. 1969 Rough wall turbulent boundary layers. J. Fluid Mech. 37 (02), 383–413.CrossRefGoogle Scholar
Raupach, M. R. 1981 Conditional statistics of Reynolds stress in rough-wall and smooth-wall turbulent boundary layers. J. Fluid Mech. 108, 363–382.Google Scholar
Raupach, M. R., Antonia, R. A. & Rajagopalan, S. 1991 Rough-wall turbulent boundary layers. Appl. Mech. Rev. 44 (1), 1–25.Google Scholar
Raupach, M. R., Thom, A. S. & Edwards, I. 1980 A wind-tunnel study of turbulent flow close to regularly arrayed rough surfaces. Boundary-Layer Meteorol. 18 (4), 373–397.Google Scholar
Schlatter, P. & Örlü, R. 2012 Turbulent boundary layers at moderate Reynolds numbers: inflow length and tripping effects. J. Fluid Mech. 710, 5–34.Google Scholar
Schultz, M. P. & Flack, K. A. 2003 Turbulent boundary layers over surfaces smoothed by sanding. Trans. ASME J. Fluids Engng 125 (5), 863–870.Google Scholar
Schultz, M. P. & Flack, K. A. 2007 The rough-wall turbulent boundary layer from the hydraulically smooth to the fully rough regime. J. Fluid Mech. 580, 381–405.Google Scholar
Shockling, M. A., Allen, J. J. & Smits, A. J. 2006 Roughness effects in turbulent pipe flow. J. Fluid Mech. 564, 267–285.Google Scholar
Sillero, J. A., Jiménez, J. & Moser, R. D. 2013 One-point statistics for turbulent wall-bounded flows at Reynolds numbers up to 𝛿+ ≈ 2000. Phys. Fluids 25 (10), 105102.Google Scholar
Smits, A. J., Monty, J., Hultmark, M., Bailey, S. C. C., Hutchins, N. & Marusic, I. 2011 Spatial resolution correction for wall-bounded turbulence measurements. J. Fluid Mech. 676, 41–53.Google Scholar
Sreenivasan, K. R. & Sahay, A.1997 The persistence of viscous effects in the overlap region, and the mean velocity in turbulent pipe and channel flows. arXiv Physics (9708016).Google Scholar
Tachie, M. F., Bergstrom, D. J. & Balachandar, R. 2000 Rough wall turbulent boundary layers in shallow open channel flow. Trans. ASME J. Fluids Engng 122 (3), 533–541.CrossRefGoogle Scholar
Talluru, K. M., Kulandaivelu, V., Hutchins, N. & Marusic, I. 2014 A calibration technique to correct sensor drift issues in hot-wire anemometry. Meas. Sci. Technol. 25 (10), 105304.CrossRefGoogle Scholar
Thom, A. S. 1971 Momentum absorption by vegetation. Q. J. R. Meteorol. Soc. 97 (414), 414–428.CrossRefGoogle Scholar
Toh, S. & Itano, T. 2005 Interaction between a large-scale structure and near-wall structures in channel flow. J. Fluid Mech. 524 (1), 249–262.Google Scholar
Townsend, A. A. 1956 The Structure of Turbulent Shear Flow, vol. 1. Cambridge University Press.Google Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow, vol. 2. Cambridge University Press.Google Scholar
Volino, R. J., Schultz, M. P. & Flack, K. A. 2007 Turbulence structure in rough- and smooth-wall boundary layers. J. Fluid Mech. 592, 263–293.Google Scholar
Walker, J. M. 2014 The application of wall similarity techniques to determine wall shear velocity in smooth and rough wall turbulent boundary layers. Trans. ASME J. Fluids Engng 136 (5), 051204.Google Scholar
Wei, T., Fife, P., Klewicki, J. C. & McMurtry, P. 2005 Properties of the mean momentum balance in turbulent boundary layer, pipe and channel flows. J. Fluid Mech. 522, 303–327.Google Scholar
Wu, Y. & Christensen, K. T. 2007 Outer-layer similarity in the presence of a practical rough-wall topography. Phys. Fluids 19 (8), 085108.Google Scholar