Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-30T20:42:42.688Z Has data issue: false hasContentIssue false
  • English
  • Français

Collective locomotion of two closely spaced self-propelled flapping plates

Published online by Cambridge University Press:  26 June 2018

Ze-Rui Peng ,
Haibo Huang Open the ORCID record for Haibo Huang [Opens in a new window]  and
Xi-Yun Lu Open the ORCID record for Xi-Yun Lu [Opens in a new window]
Ze-Rui Peng
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei, Anhui 230026, PR China
Haibo Huang
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei, Anhui 230026, PR China
Xi-Yun Lu*
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei, Anhui 230026, PR China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Energetic benefit and enhanced performance are considered among the most fascinating achievements of collective behaviours, e.g. fish schools and flying formations. The collective locomotion of two self-propelled flapping plates initially in a side-by-side arrangement is investigated numerically. Both in-phase and antiphase oscillations for the two plates are considered. It is found that the plates will spontaneously form some stable configurations as a result of the flow-mediated interaction, specifically, the staggered-following (SF) mode and the alternate-leading (AL) mode for the in-phase scenario and the moving abreast (MA) mode and the AL mode for the antiphase scenario. In the SF mode, the rear plate follows the front one with a staggered configuration. In the AL mode, the plates chase each other side-by-side alternately. In terms of propulsive speed and efficiency, the performance of the plates in the SF mode with small lateral spacing 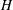$H$ is found to be better than those in the tandem following case (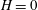$H=0$) and the side-by-side case (i.e. the AL mode). To achieve higher propulsive efficiency, no matter in-phase or antiphase oscillations, the two plates with moderate bending stiffness, e.g. 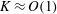$K\approx O(1)$, are preferred and they should be close enough in the lateral direction. For the side-by-side configuration, the performance of each plate in the antiphase and in-phase scenarios is enhanced and weakened in comparison with that of the isolated plate, respectively. Besides the pressure and vorticity contours, the normal force and thrust acting on the plates are also analysed. It is revealed that the thrust is mainly contributed by the normal force at moderate bending stiffness. The normal force and thrust are critical to the propulsive speed and efficiency. For two self-propelled plates, in view of hydrodynamics, to achieve higher performance the in-phase SF mode and antiphase flappings in the side-by-side configuration are preferred.

JFM classification

Biological Fluid Dynamics: Biological Fluid Dynamics Biological Fluid Dynamics: Propulsion Biological Fluid Dynamics: Swimming/flying
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 849 , 25 August 2018 , pp. 1068 - 1095
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abrahams, M. V. & Colgan, P. W. 1987 Fish schools and their hydrodynamic function: a reanalysis. Environ. Biol. Fishes 20 (1), 79–80.Google Scholar
Alben, S. 2010 Passive and active bodies in vortex-street wakes. J. Fluid Mech. 642, 95–125.Google Scholar
Ashraf, I., Bradshaw, H., Ha, T.-T., Halloy, J., Godoy-Diana, R. & Thiria, B. 2017 Simple phalanx pattern leads to energy saving in cohesive fish schooling. Proc. Natl Acad. Sci. USA 114 (36), 9599–9604.Google Scholar
Ashraf, I., Godoy-Diana, R., Halloy, J., Collignon, B. & Thiria, B. 2016 Synchronization and collective swimming patterns in fish (Hemigrammus bleheri) . J. R. Soc. Interface 13 (123), 20160734.Google Scholar
Bajec, I. L. & Heppner, F. H. 2009 Organized flight in birds. Anim. Behav. 78, 777–789.Google Scholar
Becker, A. D., Masoud, H., Newbolt, J. W., Shelley, M. & Ristroph, L. 2015 Hydrodynamic schooling of flapping swimmers. Nat. Commun. 6, 8514.Google Scholar
Boschitsch, B. M., Dewey, P. A. & Smits, A. J. 2014 Propulsive performance of unsteady tandem hydrofoils in an in-line configuration. Phys. Fluids 26, 051901.Google Scholar
Broering, T. M., Lian, Y. & Henshaw, W. 2012 Numerical investigation of energy extraction in a tandem flapping wing configuration. AIAA J. 50, 2295–2307.Google Scholar
Chen, S. & Doolen, G. D. 1998 Lattice Boltzmann method for fluid flows. Annu. Rev. Fluid Mech. 30, 329–364.Google Scholar
Connell, B. S. H. & Yue, D. K. P. 2007 Flapping dynamics of a flag in a uniform stream. J. Fluid Mech. 581, 33–67.Google Scholar
Couzin, I. D., Krause, J., Franks, N. R. & Levin, S. A. 2005 Effective leadership and decision-making in animal groups on the move. Nature 433 (7025), 513–516.Google Scholar
Couzin, I. D., Krause, J., James, R., Ruxton, G. D. & Franks, N. R. 2002 Collective memory and spatial sorting in animal groups. J. Theor. Biol. 218 (1), 1–11.Google Scholar
Daghooghi, M. & Borazjani, I. 2015 The hydrodynamic advantages of synchronized swimming in a rectangular pattern. Bioinspir. Biomim. 10 (5), 056018.Google Scholar
Dewey, P. A., Quinn, D. B., Boschitsch, B. M. & Smits, A. J. 2014 Propulsive performance of unsteady tandem hydrofoils in a side-by-side configuration. Phys. Fluids 26, 041903.Google Scholar
Dong, G.-J. & Lu, X.-Y. 2007 Characteristics of flow over traveling wavy foils in a side-by-side arrangement. Phys. Fluids 19, 057107.Google Scholar
Dong, H., Mittal, R. & Najjar, F. M. 2006 Wake topology and hydrodynamic performance of low-aspect-ratio flapping foils. J. Fluid Mech. 566, 309–343.Google Scholar
Doyle, J. F. 2001 Nonlinear Analysis of Thin-Walled Structures: Statics, Dynamics, and Stability. Springer.Google Scholar
Gazzola, M., Tchieu, A. A., Alexeev, D., de Brauer, A. & Koumoutsakos, P. 2016 Learning to school in the presence of hydrodynamic interactions. J. Fluid Mech. 789, 726–749.Google Scholar
Graves, J. 1977 Photographic method for measuring the spacing and density within pelagic fish schools at sea. U.S. Fish. Bull. 75, 230–234.Google Scholar
Guazzelli, É. & Hinch, J. 2011 Fluctuations and instability in sedimentation. Annu. Rev. Fluid Mech. 43, 97–116.Google Scholar
Hemelrijk, C. K., Reid, D. A. P., Hildenbrandt, H. & Padding, J. T. 2015 The increased efficiency of fish swimming in a school. Fish Fish. 16, 511–521.Google Scholar
Hua, R.-N., Zhu, L. & Lu, X.-Y. 2013 Locomotion of a flapping flexible plate. Phys. Fluids 25, 121901.Google Scholar
Hua, R.-N., Zhu, L. & Lu, X.-Y. 2014 Dynamics of fluid flow over a circular flexible plate. J. Fluid Mech. 759, 56–72.Google Scholar
Hummel, D. 1983 Aerodynamic aspects of formation flight in birds. J. Theor. Biol. 104, 321–347.Google Scholar
Katz, Y., Tunstrøm, K., Ioannou, C. C., Huepe, C. & Couzin, I. D. 2011 Inferring the structure and dynamics of interactions in schooling fish. Proc. Natl Acad. Sci. USA 108 (46), 18720–18725.Google Scholar
Killen, S. S., Marras, S., Steffensen, J. F. & McKenzie, D. J. 2012 Aerobic capacity influences the spatial position of individuals within fish schools. Proc. R. Soc. Lond. B 279 (1727), 357.Google Scholar
Landa, J. T. 1998 Bioeconomics of schooling fishes: selfish fish, quasi-free riders, and other fishy tales. Environ. Biol. Fishes 53 (4), 353–364.Google Scholar
Li, G.-J. & Lu, X.-Y. 2012 Force and power of flapping plates in a fluid. J. Fluid Mech. 712, 598–613.Google Scholar
Lighthill, M. J. 1975 Mathematical Biofluiddynamics, vol. 17. SIAM.Google Scholar
Lissaman, P. B. S. & Shollenberger, C. A. 1970 Formation flight of birds. Science 168, 1003–1005.Google Scholar
Major, P. F. & Dill, L. M. 1978 The three-dimensional structure of airborne bird flocks. Behav. Ecol. Sociobiol. 4 (2), 111–122.Google Scholar
Mittal, R. & Iaccarino, G. 2005 Immersed boundary methods. Annu. Rev. Fluid Mech. 37, 239–261.Google Scholar
Mysa, R. C. & Venkatraman, K. 2016 Intertwined vorticity and elastodynamics in flapping wing propulsion. J. Fluid Mech. 787, 175–223.Google Scholar
Parrish, J. K. & Edelstein-Keshet, L. 1999 Complexity, pattern, and evolutionary trade-offs in animal aggregation. Science 284, 99–101.Google Scholar
Partridge, B. L. 1982 The structure and function of fish schools. Sci. Am. 246 (6), 114–123.Google Scholar
Partridge, B. L., Pitcher, T., Cullen, J. M. & Wilson, J. 1980 The three-dimensional structure of fish schools. Behav. Ecol. Sociobiol. 6 (4), 277–288.Google Scholar
Partridge, B. L. & Pitcher, T. J. 1979 Evidence against a hydrodynamic function for fish schools. Nature 279 (5712), 418–419.Google Scholar
Peruani, F., Starruss, J., Jakovljevic, V., Søgaard-Andersen, L., Deutsch, A. & Bär, M. 2012 Collective motion and nonequilibrium cluster formation in colonies of gliding bacteria. Phys. Rev. Lett. 108, 098102.Google Scholar
Peskin, C. S. 2002 The immersed boundary method. Acta Numer. 11, 479–517.Google Scholar
Portugal, S. J., Hubel, T. Y., Fritz, J., Heese, S., Trobe, D., Voelkl, B., Hailes, S., Wilson, A. M. & Usherwood, J. R. 2014 Upwash exploitation and downwash avoidance by flap phasing in ibis formation flight. Nature 505 (7483), 399–402.Google Scholar
Ramananarivo, S., Fang, F., Oza, A., Zhang, J. & Ristroph, L. 2016 Flow interactions lead to orderly formations of flapping wings in forward flight. Phys. Rev. Fluids 1 (7), 071201.Google Scholar
Ramananarivo, S., Godoy-Diana, R. & Thiria, B. 2011 Rather than resonance, flapping wing flyers may play on aerodynamics to improve performance. Proc. Natl Acad. Sci. USA 108, 5964–5969.Google Scholar
Saintillan, D. & Shelley, M. J. 2008 Instabilities and pattern formation in active particle suspensions: kinetic theory and continuum simulations. Phys. Rev. Lett. 100, 178103.Google Scholar
Sumpter, D. 2006 The principles of collective animal behaviour. Phil. Trans. R. Soc. Lond. B 361, 5–22.Google Scholar
Thiria, B. & Godoy-Diana, R. 2010 How wing compliance drives the efficiency of self-propelled flapping flyers. Phys. Rev. E 82, 015303.Google Scholar
Vandenberghe, N., Zhang, J. & Childress, S. 2004 Symmetry breaking leads to forward flapping flight. J. Fluid Mech. 506, 147–155.Google Scholar
Viscido, S. V., Parrish, J. K. & Grünbaum, D. 2005 The effect of population size and number of influential neighbors on the emergent properties of fish schools. Ecol. Model. 183 (2), 347–363.Google Scholar
Warkentin, J. & DeLaurier, J. 2007 Experimental aerodynamic study of tandem flapping membrane wings. J. Aircraft 44, 1653–1661.Google Scholar
Weihs, D. 1973 Hydromechanics of fish schooling. Nature 241, 290–291.Google Scholar
Weihs, D. 1975 Some Hydrodynamical Aspects of Fish Schooling. Springer.Google Scholar
Zhang, H.-P., Beer, A., Florin, E.-L. & Swinney, H. 2010 Collective motion and density fluctuations in bacterial colonies. Proc. Natl Acad. Sci. USA 107, 13626–13630.Google Scholar
Zhu, X., He, G. & Zhang, X. 2014a Flow-mediated interactions between two self-propelled flapping filaments in tandem configuration. Phys. Rev. Lett. 113, 238105.Google Scholar
Zhu, X., He, G. & Zhang, X. 2014b How flexibility affects the wake symmetry properties of a self-propelled plunging foil. J. Fluid Mech. 751, 164–183.Google Scholar
Zou, Q. & He, X. 1997 On pressure and velocity boundary conditions for the lattice Boltzmann BGK model. Phys. Fluids 9 (6), 1591–1598.Google Scholar