Article contents
Collapse of a neutrally buoyant suspension column: from Newtonian to apparent non-Newtonian flow regimes
Published online by Cambridge University Press: 15 August 2017
Abstract
Experiments on the collapse of non-colloidal and neutrally buoyant particles suspended in a Newtonian fluid column are presented, in which the initial volume fraction of the suspension
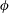 $\unicode[STIX]{x1D719}$
, the viscosity of the interstitial fluid
$\unicode[STIX]{x1D719}$
, the viscosity of the interstitial fluid
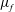 $\unicode[STIX]{x1D707}_{f}$
, the diameter of the particles
$\unicode[STIX]{x1D707}_{f}$
, the diameter of the particles
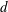 $d$
and the mixing protocol, i.e. the initial preparation of the suspension, are varied. The temporal evolution of the slumping current highlights two main regimes: (i) an inertial-dominated regime followed by (ii) a viscous-dominated regime. The inertial regime is characterized by a constant-speed slumping which is shown to scale as in the case of a classical inertial dam-break. The viscous-dominated regime is observed as a decreasing-speed phase of the front evolution. Lubrication models for Newtonian and power-law fluids describe most of situations encountered in this regime, which strongly depends on the suspension parameters. The temporal evolution of the propagating front is used to extract the rheological parameters of the fluid models. At the early stages of the viscous-dominated regime, a constant effective shear viscosity, referred to as an apparent Newtonian viscous regime, is found to depend only on
$d$
and the mixing protocol, i.e. the initial preparation of the suspension, are varied. The temporal evolution of the slumping current highlights two main regimes: (i) an inertial-dominated regime followed by (ii) a viscous-dominated regime. The inertial regime is characterized by a constant-speed slumping which is shown to scale as in the case of a classical inertial dam-break. The viscous-dominated regime is observed as a decreasing-speed phase of the front evolution. Lubrication models for Newtonian and power-law fluids describe most of situations encountered in this regime, which strongly depends on the suspension parameters. The temporal evolution of the propagating front is used to extract the rheological parameters of the fluid models. At the early stages of the viscous-dominated regime, a constant effective shear viscosity, referred to as an apparent Newtonian viscous regime, is found to depend only on
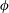 $\unicode[STIX]{x1D719}$
and
$\unicode[STIX]{x1D719}$
and
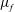 $\unicode[STIX]{x1D707}_{f}$
for each mixing protocol. The obtained values are shown to be well fitted by the Krieger–Dougherty model whose parameters involved, say a critical volume fraction
$\unicode[STIX]{x1D707}_{f}$
for each mixing protocol. The obtained values are shown to be well fitted by the Krieger–Dougherty model whose parameters involved, say a critical volume fraction
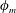 $\unicode[STIX]{x1D719}_{m}$
and the exponent of divergence, depend on the mixing protocol, i.e. the microscale interaction between particles. On a longer time scale which depends on
$\unicode[STIX]{x1D719}_{m}$
and the exponent of divergence, depend on the mixing protocol, i.e. the microscale interaction between particles. On a longer time scale which depends on
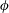 $\unicode[STIX]{x1D719}$
, the front evolution is shown to slightly deviate from the apparent Newtonian model. In this apparent non-Newtonian viscous regime, the power-law model, indicating both shear-thinning and shear-thickening behaviours, is shown to be more appropriate to describe the front evolution. The present experiments indicate that the mixing protocol plays a crucial role in the selection of a shear-thinning or shear-thickening type of collapse, while the particle diameter
$\unicode[STIX]{x1D719}$
, the front evolution is shown to slightly deviate from the apparent Newtonian model. In this apparent non-Newtonian viscous regime, the power-law model, indicating both shear-thinning and shear-thickening behaviours, is shown to be more appropriate to describe the front evolution. The present experiments indicate that the mixing protocol plays a crucial role in the selection of a shear-thinning or shear-thickening type of collapse, while the particle diameter
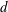 $d$
and volume fraction
$d$
and volume fraction
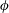 $\unicode[STIX]{x1D719}$
play a significant role in the shear-thickening case. In all cases, the normalized effective consistency of the power-law fluid model is found to be a unique function of
$\unicode[STIX]{x1D719}$
play a significant role in the shear-thickening case. In all cases, the normalized effective consistency of the power-law fluid model is found to be a unique function of
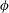 $\unicode[STIX]{x1D719}$
. Finally, an apparent viscoplastic regime, characterized by a finite length spreading reached at finite time, is observed at high
$\unicode[STIX]{x1D719}$
. Finally, an apparent viscoplastic regime, characterized by a finite length spreading reached at finite time, is observed at high
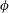 $\unicode[STIX]{x1D719}$
. This regime is mostly observed for volume fractions larger than
$\unicode[STIX]{x1D719}$
. This regime is mostly observed for volume fractions larger than
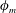 $\unicode[STIX]{x1D719}_{m}$
and up to a volume fraction
$\unicode[STIX]{x1D719}_{m}$
and up to a volume fraction
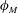 $\unicode[STIX]{x1D719}_{M}$
close to the random close packing fraction at which the initial column remains undeformed on opening the gate.
$\unicode[STIX]{x1D719}_{M}$
close to the random close packing fraction at which the initial column remains undeformed on opening the gate.
- Type
- Papers
- Information
- Copyright
- © 2017 Cambridge University Press
References
- 15
- Cited by



