Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-12-01T04:04:32.477Z Has data issue: false hasContentIssue false
  • English
  • Français

Coherent structures in a swirl injector at Re = 4800 by nonlinear simulations and linear global modes

Published online by Cambridge University Press:  03 March 2016

O. Tammisola  and
M. P. Juniper
O. Tammisola*
Affiliation:
Faculty of Engineering, The University of Nottingham, NG7 2RD, UK KTH Mechanics, KTH Royal Institute of Technology, SE-10044 Stockholm, Sweden
M. P. Juniper
Affiliation:
Department of Engineering, University of Cambridge, Cambridge CB2 1PZ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The large-scale coherent motions in a realistic swirl fuel-injector geometry are analysed by direct numerical simulations (DNS), proper orthogonal decomposition (POD), and linear global modes. The aim is to identify the origin of instability in this turbulent flow in a complex internal geometry. The flow field in the nonlinear simulation is highly turbulent, but with a distinguishable coherent structure: the precessing vortex core (a spiralling mode). The most energetic POD mode pair is identified as the precessing vortex core. By analysing the fast Fourier transform (FFT) of the time coefficients of the POD modes, we conclude that the first four POD modes contain the coherent fluctuations. The remaining POD modes (incoherent fluctuations) are used to form a turbulent viscosity field, using the Newtonian eddy model. The turbulence sets in from convective shear layer instabilities even before the nonlinear flow reaches the other end of the domain, indicating that equilibrium solutions of the Navier–Stokes are never observed. Linear global modes are computed around the mean flow from DNS, applying the turbulent viscosity extracted from POD modes. A slightly stable discrete 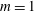$m=1$ eigenmode is found, well separated from the continuous spectrum, in very good agreement with the POD mode shape and frequency. The structural sensitivity of the precessing vortex core is located upstream of the central recirculation zone, identifying it as a spiral vortex breakdown instability in the nozzle. Furthermore, the structural sensitivity indicates that the dominant instability mechanism is the Kelvin–Helmholtz instability at the inflection point forming near vortex breakdown. Adjoint modes are strong in the shear layer along the whole extent of the nozzle, showing that the optimal initial condition for the global mode is localized in the shear layer. We analyse the qualitative influence of turbulent dissipation in the stability problem (eddy viscosity) on the eigenmodes by comparing them to eigenmodes computed without eddy viscosity. The results show that the eddy viscosity improves the complex frequency and shape of global modes around the fuel-injector mean flow, while a qualitative wavemaker position can be obtained with or without turbulent dissipation, in agreement with previous studies. This study shows how sensitivity analysis can identify which parts of the flow in a complex geometry need to be altered in order to change its hydrodynamic stability characteristics.

JFM classification

Instability: Absolute/convective instability Flow Control: Mixing enhancement Vortex Flows: Vortex breakdown
Type
Papers
Information
Journal of Fluid Mechanics , Volume 792 , 10 April 2016 , pp. 620 - 657
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barkley, D. 2006 Linear analysis of the cylinder wake mean flow. Europhys. Lett. 75, 750–756.Google Scholar
Beran, P. S. 1994 The time-asymptotic behavior of vortex breakdown in tubes. Comput. Fluids 23, 913–937.Google Scholar
Billant, P., Chomaz, J.-M. & Huerre, P. 1998 Experimental study of vortex breakdown in swirling jets. J. Fluid Mech. 376, 183–219.Google Scholar
Camarri, S., Fallenius, B. & Fransson, J. 2013 Stability analysis of experimental flow fields behind a porous cylinder for the investigation of the large-scale wake vortices. J. Fluid Mech. 715, 499–536.Google Scholar
Chomaz, J.-M. 2005 Global instabilities in spatially developing flows: non-normality and nonlinearity. Annu. Rev. Fluid Mech. 37, 357–392.Google Scholar
Cohen, J. & Wygnanski, I. 1987 The evolution of instabilities in the axisymmetrical jet. Part 1. The linear growth of disturbances near the nozzle. J. Fluid Mech. 176, 191–219.CrossRefGoogle Scholar
Conroy, D., Moisala, A., Cardoso, S., Windle, A. & Davidson, J. 2010 Carbon nanotube reactor: ferrocene decomposition, iron particle growth, nanotube aggregation and scale-up. Chem. Engng Sci. 65, 2965–2977.Google Scholar
Crouch, J. D., Garbaruk, A. & Magidov, D. 2007 Prediction of the flow unsteadiness based on global instability. J. Comput. Phys. 224, 924–940.Google Scholar
Dunham, D., Spencer, A., McGuirk, J. J. & Dianat, M. 2008 Comparison of unsteady Reynolds averaged Navier–Stokes and large eddy simulation computational fluid dynamics methodologies for air swirl fuel injectors. Trans. ASME: J. Engng Gas Turbines Power 131 (1), 011502.Google Scholar
El-Khoury, G., Schlatter, P., Noorani, A., Fischer, P. F., Breethouwer, G. & Johansson, A. V. 2013 Direct numerical simulation of turbulent pipe flows at moderately high Reynolds numbers. Flow Turbul. Combust. 91, 475–495.Google Scholar
Fischer, P. F. 1997 An overlapping Schwarz method for spectral element solution of the incompressible Navier–Stokes equations. J. Comput. Phys. 133, 84–101.Google Scholar
Fischer, P. F., Lottes, J. W. & Kerkemeier, S. G.2008 nek5000 Web page.http://nek5000.mcs.anl.gov.Google Scholar
Gallaire, F., Ruith, M., Meiburg, E., Chomaz, J.-M. & Huerre, P. 2006 Spiral vortex breakdown as a global mode. J. Fluid Mech. 549, 71–80.Google Scholar
Gaster, M., Kit, E. & Wygnanski, I. 1985 Large-scale structures in a forced turbulent mixing layer. J. Fluid Mech. 150, 23–39.CrossRefGoogle Scholar
Giannetti, F. & Luchini, P. 2007 Structural sensitivity of the first instability of the cylinder wake. J. Fluid Mech. 581, 167–197.CrossRefGoogle Scholar
Grabowski, W. J. & Berger, S. A. 1976 Solutions of the Navier–Stokes equations for vortex breakdown. J. Fluid Mech. 75, 525–544.Google Scholar
Gupta, V.2014 Linear amplification analysis for extraction of coherent structures in wall-bounded turbulent flows. PhD thesis, University of Cambridge.Google Scholar
Hansford, S., OĆonnor, J., Manoharan, K. & Hemchandra, S. 2015 Impact of flow non-axisymmetry on swirling flow dynamics and receptivity to acoustics. In Proceedings of ASME Turbo Expo, pp. GT2015–43377.Google Scholar
Hecht, F. 2012 New development in FreeFem++. J. Numer. Math. 20, 251–265.Google Scholar
Hoyas, S. & Jimenez, J. 2006 Scaling of the velocity fluctuations in turbulent channels up to $Re_{{\it\tau}}=2003$ . Phys. Fluids 18, 011702.Google Scholar
Juniper, M. P. 2012 Absolute and convective instability in gas turbine fuel injectors. In Proceedings of ASME Turbo Expo 2012, pp. GT2012–68253.Google Scholar
Juniper, M. P. & Pier, B. 2014 The structural sensitivity of open shear flows calculated by local stability analysis. Eur. J. Mech. (B/Fluids) 49, 426–437.Google Scholar
Lashgari, I., Tammisola, O., Citro, V., Brandt, L. & Juniper, M. P. 2014 The planar X-junction flow: stability and control. J. Fluid Mech. 753, 1–28.CrossRefGoogle Scholar
Leibovich, S. 1978 The structure of vortex breakdown. Annu. Rev. Fluid Mech. 10, 221–246.Google Scholar
Lieuwen, T. C. 2012 Unsteady Combustor Physics. Chap. 4, Cambridge University Press.Google Scholar
Luchtenburg, D. M., Günther, B., Noack, B. R., King, R. & Tadmor, G. 2009 A generalized mean field model of the natural and high-frequency actuated flow around a high-lift configuration. J. Fluid Mech. 623, 283–316.Google Scholar
Maday, Y. & Patera, A. T. 1989 Spectral element methods for the Navier–Stokes equations. In State-of-the-art Surveys on Computational Mechanics (ed. Noor, A.), pp. 71–143. ASME.Google Scholar
Manoharan, K., Hansford, S., OĆonnor, J. & Hemchandra, S. 2015 Instability mechanism in a swirl flow combustor: precession of vortex core and influence of density gradient. In Proceedings of ASME Turbo Expo, pp. GT2015–42985.Google Scholar
Meliga, P., Gallaire, F. & Chomaz, J.-M. 2012a A weakly nonlinear mechanism for mode selection in swirling jets. J. Fluid Mech. 699, 216–262.Google Scholar
Meliga, P., Pujals, G. & Serre, E. 2012b Sensitivity of 2-d turbulent flow past a D-shaped cylinder using global stability. Phys. Fluids 24, 061701.Google Scholar
Mettot, C., Renac, F. & Sipp, D. 2014a Computation of eigenvalue sensitivity in a discrete framework: application to open-loop control. J. Comput. Phys. 269, 234–258.Google Scholar
Mettot, C., Sipp, D. & Bézard, H. 2014b Quasi-laminar stability and sensitivity analyses for turbulent flows: prediction of low-frequency unsteadiness and passive control. Phys. Fluids 26, 045112.Google Scholar
Mezic, I. 2013 Analysis of fluid flows via the spectral properties of the Koopman operator. Annu. Rev. Fluid Mech. 45, 357–378.CrossRefGoogle Scholar
Midgley, K., Spencer, A. & McGuirk, J. J. 2005 Unsteady flow structures in swirler fed fuel injectors. Trans. ASME: J. Engng Gas Turbines Power 127, 755–764.Google Scholar
Noack, B. R., Afanasiev, K., Morzynski, M., Tadmor, G. & Thiele, F. 2003 A hierarchy of low-dimensional models for the transient and post-transient cylinder wake. J. Fluid Mech. 497, 335–363.Google Scholar
Oberleithner, K., Paschereit, C. & Wygnanski, I. 2014a On the impact of swirl on the growth of coherent structures. J. Fluid Mech. 741, 156–199.Google Scholar
Oberleithner, K., Rukes, L. & Soria, J. 2014b Mean flow stability analysis of oscillating jet experiments. J. Fluid Mech. 757, 1–32.Google Scholar
Oberleithner, K., Sieber, M. & Nayeri, C. 2011 Three-dimensional coherent structures in a swirling jet undergoing vortex breakdown: stability analysis and empirical mode. J. Fluid Mech. 679, 383–414.Google Scholar
Oberleithner, K., Stöhr, M., Im, S. H., Arndt, C. M. & Steinberg, A. M. 2015 Formation and flame-induced suppression of the precessing vortex core in a swirl combustor: experiments and linear stability analysis. Combust. Flame 162, 3100–3114.Google Scholar
Ohlsson, J., Schlatter, P., Fischer, P. F. & Henningson, D. S. 2010 Direct numerical simulation of separated flow in a three-dimensional diffuser. J. Fluid Mech. 650, 307–318.Google Scholar
Östh, J., Noack, B. R., Krajnovic, S., Barros, D. & Bore, J. 2014 On the need for a nonlinear subscale turbulence term in pod models as exemplified for a high-Reynolds-number flow over an ahmed body. J. Fluid Mech. 747, 518–544.Google Scholar
Parezanovic, V. & Cadot, O. 2012 Experimental sensitivity analysis of the global properties of a two-dimensional turbulent wake. J. Fluid Mech. 693, 115–149.Google Scholar
Protas, B., Noack, B. R. & Östh, J. 2015 Optimal nonlinear eddy viscosity in Galerkin models of turbulent flows. J. Fluid Mech. 766, 337–367.Google Scholar
Pujals, G., Garcia-Villalba, M., Cossu, C. & Depardon, S. 2009 A note on optimal transient growth in turbulent channel flows. Phys. Fluids 21, 015109.Google Scholar
Qadri, U. A., Mistry, D. & Juniper, M. P. 2013 Structural sensitivity of spiral vortex breakdown. J. Fluid Mech. 720, 558–581.Google Scholar
Revuelta, A. 2004 On the axisymmetric vortex breakdown of a swirling jet entering a sudden expansion pipe. Phys. Fluids 16, 3495–3498.Google Scholar
Reynolds, W. C. & Hussain, A. K. M. F. 1972 The mechanics of an organized wave in turbulent shear flow. Part 3. Theoretical models and comparisons with experiments. J. Fluid Mech. 54 (2), 263–288.Google Scholar
Ruith, M. R., Chen, P., Meiburg, E. & Maxworthy, T. 2003 Three-dimensional vortex breakdown in swirling jets and wakes: direct numerical simulation. J. Fluid Mech. 486, 331–378.CrossRefGoogle Scholar
Schmid, P. J. & Henningson, D. S. 2001 Stability and Transition in Shear Flows. Springer.Google Scholar
Sipp, D. & Lebedev, A. 2007 Global stability of base and mean flows: a general approach and its applications to cylinder and open cavity flows. J. Fluid Mech. 593, 333–358.Google Scholar
Stuart, J. T. 1958 On the non-linear mechanics of hydrodynamic stability. J. Fluid Mech. 4, 1–21.Google Scholar
Stuart, J. T. 1971 Nonlinear stability theory. Annu. Rev. Fluid Mech. 3, 347–370.Google Scholar
Syred, N. 2006 A review of oscillation mechanisms and the role of the precessing vortex core (PVC) in swirl combustion systems. Prog. Energy Combust. Sci. 32, 93–161.Google Scholar
Tammisola, O. 2012 Oscillatory sensitivity patterns for global modes in wakes. J. Fluid Mech. 701, 251–277.Google Scholar
Tammisola, O., Giannetti, F., Citro, V. & Juniper, M. P. 2014 Second-order perturbation of global modes and implications for spanwise wavy actuation. J. Fluid Mech. 755, 314–335.Google Scholar
Turton, S. E., Tuckerman, L. & Barkley, D. 2015 Prediction of frequencies in thermosolutal convection from mean flows. Phys. Rev. E 91, 043009.Google Scholar
Wallin, S. & Johansson, A. V. 2000 An explicit algebraic reynolds stress model for incompressible and compressible turbulent flows. J. Fluid Mech. 403, 89–132.Google Scholar
Weisbrot, I. & Wygnanski, I. 1988 On coherent structures in a highly excited mixing layer. J. Fluid Mech. 195, 137–159.Google Scholar