Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Encinar, Miguel P.
and
Jiménez, Javier
2019.
Logarithmic-layer turbulence: A view from the wall.
Physical Review Fluids,
Vol. 4,
Issue. 11,
Illingworth, Simon J.
2020.
Streamwise-constant large-scale structures in Couette and Poiseuille flows.
Journal of Fluid Mechanics,
Vol. 889,
Issue. ,
McMullen, Ryan M.
Rosenberg, Kevin
and
McKeon, Beverley J.
2020.
Interaction of forced Orr-Sommerfeld and Squire modes in a low-order representation of turbulent channel flow.
Physical Review Fluids,
Vol. 5,
Issue. 8,
Hwang, Yongyun
and
Eckhardt, Bruno
2020.
Attached eddy model revisited using a minimal quasi-linear approximation.
Journal of Fluid Mechanics,
Vol. 894,
Issue. ,
Liu, Chang
and
Gayme, Dennice F.
2020.
An input–output based analysis of convective velocity in turbulent channels.
Journal of Fluid Mechanics,
Vol. 888,
Issue. ,
Bhatt, S.
and
Gnanamanickam, E.
2020.
Linear and nonlinear mechanisms within a forced plane wall jet.
Physical Review Fluids,
Vol. 5,
Issue. 7,
Gatti, Davide
Chiarini, Alessandro
Cimarelli, Andrea
and
Quadrio, Maurizio
2020.
Structure function tensor equations in inhomogeneous turbulence.
Journal of Fluid Mechanics,
Vol. 898,
Issue. ,
Symon, S.
Illingworth, S. J.
and
Marusic, I.
2020.
Large-scale structures predicted by linear models of wall-bounded turbulence.
Journal of Physics: Conference Series,
Vol. 1522,
Issue. 1,
p.
012006.
Koo, Bonguk
and
Kang, Yong-Duck
2020.
Control of Synthetic Hairpin Vortices in Laminar Boundary Layer for Skin-Friction Reduction.
Journal of Marine Science and Engineering,
Vol. 8,
Issue. 1,
p.
45.
Deshpande, Rahul
de Silva, Charitha M.
Lee, Myoungkyu
Monty, Jason P.
and
Marusic, Ivan
2021.
Data-driven enhancement of coherent structure-based models for predicting instantaneous wall turbulence.
International Journal of Heat and Fluid Flow,
Vol. 92,
Issue. ,
p.
108879.
Sun, Guangrui
Wan, Dongdong
and
Zhang, Mengqi
2021.
Nonlinear evolutions of streaky structures in viscoelastic pipe flows.
Journal of Non-Newtonian Fluid Mechanics,
Vol. 295,
Issue. ,
p.
104622.
Liu, Chang
and
Gayme, Dennice F.
2021.
Structured input–output analysis of transitional wall-bounded flows.
Journal of Fluid Mechanics,
Vol. 927,
Issue. ,
Oehler, Stephan F.
and
Illingworth, Simon J.
2021.
Linear control of coherent structures in wall-bounded turbulence at Reτ=2000.
International Journal of Heat and Fluid Flow,
Vol. 87,
Issue. ,
p.
108735.
Deshpande, Rahul
Monty, Jason P.
and
Marusic, Ivan
2021.
Active and inactive components of the streamwise velocity in wall-bounded turbulence.
Journal of Fluid Mechanics,
Vol. 914,
Issue. ,
Skouloudis, Nikolaos
and
Hwang, Yongyun
2021.
Scaling of turbulence intensities up to
Reτ=106
with a resolvent-based quasilinear approximation.
Physical Review Fluids,
Vol. 6,
Issue. 3,
Li, Wu
Akinyemi, Lanre
Lu, Dianchen
and
Khater, Mostafa M. A.
2021.
Abundant Traveling Wave and Numerical Solutions of Weakly Dispersive Long Waves Model.
Symmetry,
Vol. 13,
Issue. 6,
p.
1085.
Chu, Yuming
Khater, Mostafa M. A.
and
Hamed, Y. S.
2021.
Diverse novel analytical and semi-analytical wave solutions of the generalized (2+1)-dimensional shallow water waves model.
AIP Advances,
Vol. 11,
Issue. 1,
Gupta, Vikrant
Madhusudanan, Anagha
Wan, Minping
Illingworth, Simon J.
and
Juniper, Matthew P.
2021.
Linear-model-based estimation in wall turbulence: improved stochastic forcing and eddy viscosity terms.
Journal of Fluid Mechanics,
Vol. 925,
Issue. ,
Aggarwal, Riya
Ugail, Hassan
and
Jha, Ravi Kumar
2022.
A deep artificial neural network architecture for mesh free solutions of nonlinear boundary value problems.
Applied Intelligence,
Vol. 52,
Issue. 1,
p.
916.
Nikolaidis, Marios-Andreas
Ioannou, Petros J.
Farrell, Brian F.
and
Lozano-Durán, Adrián
2023.
POD-based study of turbulent plane Poiseuille flow: comparing structure and dynamics between quasi-linear simulations and DNS.
Journal of Fluid Mechanics,
Vol. 962,
Issue. ,
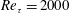 $Re_{\unicode[STIX]{x1D70F}}=2000$ is considered. We use the two-dimensional (2-D) linear coherence spectrum (LCS) to perform the comparison over a wide range of energy-carrying streamwise and spanwise length scales. The study of the 2-D LCS from DNS indicates the presence of large-scale structures that are coherent over large wall-normal distances and that are self-similar. We find that, with the addition of an eddy viscosity profile, these features of the large-scale structures are captured by the linearized equations, except in the region close to the wall. To further study this coherence, a coherence-based estimation technique, spectral linear stochastic estimation, is used to build linear estimators from the linearized Navier–Stokes equations. The estimator uses the instantaneous streamwise velocity field or the 2-D streamwise energy spectrum at one wall-normal location (obtained from DNS) to predict the same quantity at a different wall-normal location. We find that the addition of an eddy viscosity profile significantly improves the estimation.
$Re_{\unicode[STIX]{x1D70F}}=2000$ is considered. We use the two-dimensional (2-D) linear coherence spectrum (LCS) to perform the comparison over a wide range of energy-carrying streamwise and spanwise length scales. The study of the 2-D LCS from DNS indicates the presence of large-scale structures that are coherent over large wall-normal distances and that are self-similar. We find that, with the addition of an eddy viscosity profile, these features of the large-scale structures are captured by the linearized equations, except in the region close to the wall. To further study this coherence, a coherence-based estimation technique, spectral linear stochastic estimation, is used to build linear estimators from the linearized Navier–Stokes equations. The estimator uses the instantaneous streamwise velocity field or the 2-D streamwise energy spectrum at one wall-normal location (obtained from DNS) to predict the same quantity at a different wall-normal location. We find that the addition of an eddy viscosity profile significantly improves the estimation.


