Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-12-01T02:48:29.953Z Has data issue: false hasContentIssue false
  • English
  • Français

Clustering and preferential concentration of finite-size particles in forced homogeneous-isotropic turbulence

Published online by Cambridge University Press:  11 January 2017

Markus Uhlmann Open the ORCID record for Markus Uhlmann [Opens in a new window]  and
Agathe Chouippe
Markus Uhlmann*
Affiliation:
Institute for Hydromechanics, Karlsruhe Institute of Technology, 76131 Karlsruhe, Germany
Agathe Chouippe
Affiliation:
Institute for Hydromechanics, Karlsruhe Institute of Technology, 76131 Karlsruhe, Germany
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We have performed interface-resolved direct numerical simulations of forced homogeneous-isotropic turbulence in a dilute suspension of spherical particles in the Reynolds number range 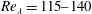$Re_{\unicode[STIX]{x1D706}}=115{-}140$. The solid–fluid density ratio was set to 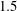$1.5$, gravity was set to zero and two particle diameters were investigated corresponding to approximately 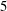$5$ and 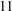$11$ Kolmogorov lengths. Note that these particle sizes are clearly outside the range of validity of the point-particle approximation, as has been shown by Homann & Bec (J. Fluid Mech., vol. 651, 2010, pp. 81–91). At the present parameter points the global effect of the particles upon the fluid flow is weak. We observe that the dispersed phase exhibits clustering with moderate intensity. The tendency to cluster, which was quantified in terms of the standard deviation of Voronoï cell volumes, decreases with the particle diameter. We have analysed the relation between particle locations and the location of intense vortical flow structures. The results do not reveal any significant statistical correlation. Contrarily, we have detected a small but statistically significant preferential location of particles with respect to the ‘sticky points’ proposed by Goto & Vassilicos (Phys. Rev. Lett., vol. 100 (5), 2008, 054503), i.e. points where the fluid acceleration field is acting such as to increase the local particle concentration in one-way coupled point-particle models under Stokes drag. The presently found statistical correlation between the ‘sticky points’ and the particle locations further increases when focusing on regions with high local concentration. Our results suggest that small finite-size particles can be brought together along the expansive directions of the fluid acceleration field, as previously observed only for the simplest model for sub-Kolmogorov particles. We further discuss the effect of density ratio and collective particle motion upon the basic Eulerian and Lagrangian statistics.

JFM classification

Turbulent Flows: Isotropic turbulence Multiphase and Particle-laden Flows: Multiphase and Particle-laden Flows Turbulent Flows: Turbulence simulation
Type
Papers
Information
Journal of Fluid Mechanics , Volume 812 , 10 February 2017 , pp. 991 - 1023
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aliseda, A., Cartellier, A., Hainaux, F. & Lasheras, J. C. 2002 Effect of preferential concentration on the settling velocity of heavy particles in homogeneous isotropic turbulence. J. Fluid Mech. 468, 77–105.CrossRefGoogle Scholar
Bagchi, P. & Balachandar, S. 2003 Effect of turbulence on the drag and lift of a particle. Phys. Fluids 15 (11), 3496–3513.CrossRefGoogle Scholar
Balachandar, S. & Eaton, J. K. 2010 Turbulent dispersed multiphase flow. Annu. Rev. Fluid Mech. 42, 111–133.CrossRefGoogle Scholar
Bec, J., Biferale, L., Boffetta, G., Celani, A., Cencini, M., Lanotte, A., Musacchio, S. & Toschi, F. 2006 Acceleration statistics of heavy particles in turbulence. J. Fluid Mech. 550 (1), 349–358.CrossRefGoogle Scholar
Bragg, A. D. & Collins, L. R. 2014 New insights from comparing statistical theories for inertial particles in turbulence: I. Spatial distribution of particles. New J. Phys. 16 (5), 055013.Google Scholar
Bragg, A. D., Ireland, P. J. & Collins, L. R. 2015a Mechanisms for the clustering of inertial particles in the inertial range of isotropic turbulence. Phys. Rev. E 92, 023029.Google ScholarPubMed
Bragg, A. D., Ireland, P. J. & Collins, L. R. 2015b On the relationship between the non-local clustering mechanism and preferential concentration. J. Fluid Mech. 780, 327–343.CrossRefGoogle Scholar
Brown, R. D., Warhaft, Z. & Voth, G. A. 2009 Acceleration statistics of neutrally buoyant spherical particles in intense turbulence. Phys. Rev. Lett. 103, 194501.CrossRefGoogle ScholarPubMed
Calzavarini, E., Kerscher, M., Lohse, D. & Toschi, F. 2008 Dimensionality and morphology of particle and bubble clusters in turbulent flow. J. Fluid Mech. 607, 13–24.CrossRefGoogle Scholar
Calzavarini, E., Volk, R., Bourgoin, M., Lévéque, E., Pinton, J.-F. & Toschi, F. 2009 Acceleration statistics of finite-sized particles in turbulent flow: the role of Faxén forces. J. Fluid Mech. 630, 179–189.CrossRefGoogle Scholar
Chen, L., Goto, S. & Vassilicos, J. C. 2006 Turbulent clustering of stagnation points and inertial particles. J. Fluid Mech. 553, 143–154.CrossRefGoogle Scholar
Chouippe, A. & Uhlmann, M. 2015 Forcing homogeneous turbulence in DNS of particulate flow with interface resolution and gravity. Phys. Fluids 27 (12), 123301.CrossRefGoogle Scholar
Chun, J., Koch, D. L., Rani, S. L., Ahluwalia, A. & Collins, L. R. 2005 Clustering of aerosol particles in isotropic turbulence. J. Fluid Mech. 536, 219–251.CrossRefGoogle Scholar
Cisse, M.2015 Suspensions turbulentes de particules de tailles finies: dynamique, modifications de l’écoulement et effets collectifs. PhD thesis, Université de Nice-Sophia Antipolis (in French).Google Scholar
Cisse, M., Homann, H. & Bec, J. 2013 Slipping motion of large neutrally buoyant particles in turbulence. J. Fluid Mech. 735, R1.CrossRefGoogle Scholar
Coleman, S. W. & Vassilicos, J. C. 2009 A unified sweep-stick mechanism to explain particle clustering in two-and three-dimensional homogeneous, isotropic turbulence. Phys. Fluids 21 (11), 113301.CrossRefGoogle Scholar
Daitche, A. 2015 On the role of the history force for inertial particles in turbulence. J. Fluid Mech. 782, 567–593.CrossRefGoogle Scholar
Doychev, T. & Uhlmann, M. 2010 A numerical study of finite size particles in homogeneous turbulent flow. In Proceedings of the 7th International Conference on Multiphase Flow (ed. Balachandar, S. & Sinclair Curtis, J.). ICMF.Google Scholar
Eaton, J. K. & Fessler, J. R. 1994 Preferential concentration of particles by turbulence. Intl J. Multiphase Flow 20 (Suppl.), 169–209.CrossRefGoogle Scholar
Eswaran, V. & Pope, S. B. 1988 An examination of forcing in direct numerical simulations of turbulence. Comput. Fluids 16 (3), 257–278.CrossRefGoogle Scholar
Fallon, T. & Rogers, B. C. 2002 Turbulence-induced preferential concentration of solid particles in microgravity conditions. Exp. Fluids 33 (2), 233–241.CrossRefGoogle Scholar
Ferenc, J.-S. & Neda, Z. 2007 On the size distribution of Poisson Voronoi cells. Physica A 385, 518–526.CrossRefGoogle Scholar
Fiabane, L., Zimmermann, R., Volk, R., Pinton, J.-F. & Bourgoin, M. 2012 Clustering of finite-size particles in turbulence. Phys. Rev. E 86, 035301(R).Google ScholarPubMed
García-Villalba, M., Kidanemariam, A. G. & Uhlmann, M. 2012 DNS of vertical plane channel flow with finite-size particles: Voronoi analysis, acceleration statistics and particle-conditioned averaging. Intl J. Multiphase Flow 46, 54–74.CrossRefGoogle Scholar
Glowinski, R., Pan, T.-W., Hesla, T. I. & Joseph, D. D. 1999 A distributed Lagrange multiplier/fictitious domain method for particulate flows. Intl J. Multiphase Flow 25, 755–794.CrossRefGoogle Scholar
Goto, S. & Vassilicos, J. C. 2006 Self-similar clustering of inertial particles and zero-acceleration points in fully developed two-dimensional turbulence. Phys. Fluids 18 (11), 115103.CrossRefGoogle Scholar
Goto, S. & Vassilicos, J. C. 2008 Sweep-stick mechanism of heavy particle clustering in fluid turbulence. Phys. Rev. Lett. 100 (5), 054503.CrossRefGoogle ScholarPubMed
Gustavsson, K. & Mehlig, B. 2016 Statistical models for spatial patterns of heavy particles in turbulence. Adv. Phys. 65 (1), 1–57.CrossRefGoogle Scholar
Hogan, R. C. & Cuzzi, J. N. 2001 Stokes and Reynolds number dependence of preferential particle concentration in simulated three-dimensional turbulence. Phys. Fluids 13 (10), 2938–2945.CrossRefGoogle Scholar
Homann, H. & Bec, J. 2010 Finite-size effects in the dynamics of neutrally buoyant particles in turbulent flow. J. Fluid Mech. 651, 81–91.CrossRefGoogle Scholar
Hunt, J. C. R., Wray, A. A. & Moin, P. 1988 Eddies, streams, and convergence zones in turbulent flows. In Proceedings of the Summer Program, pp. 193–208. Center for Turbulence Research, Stanford.Google Scholar
Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.CrossRefGoogle Scholar
Jiménez, J. 1998 Turbulent velocity fluctuations need not be Gaussian. J. Fluid Mech. 376, 139–147.CrossRefGoogle Scholar
Jiménez, J., Wray, A. A., Saffman, P. G. & Rogallo, R. S. 1993 The structure of intense vorticity in isotropic turbulence. J. Fluid Mech. 255, 65–90.CrossRefGoogle Scholar
Kidanemariam, A. G., Chan-Braun, C., Doychev, T. & Uhlmann, M. 2013 DNS of horizontal open channel flow with finite-size, heavy particles at low solid volume fraction. New J. Phys. 15 (2), 025031.CrossRefGoogle Scholar
Kidanemariam, A. G. & Uhlmann, M. 2014 Interface-resolved direct numerical simulation of the erosion of a sediment bed sheared by laminar flow. Intl J. Multiphase Flow 67, 174–188.CrossRefGoogle Scholar
Klein, S., Gibert, M., Bérut, A. & Bodenschatz, E. 2012 Simultaneous 3D measurement of the translation and rotation of finite-size particles and the flow field in a fully developed turbulent water flow. Meas. Sci. Technol. 24 (2), 024006.Google Scholar
Lomholt, S. & Maxey, M. R. 2003 Force-coupling method for particulate two-phase flow: Stokes flow. J. Comput. Phys. 184 (2), 381–405.CrossRefGoogle Scholar
Lucci, F., Ferrante, A. & Elghobashi, S. 2010 Modulation of isotropic turbulence by particles of Taylor length-scale size. J. Fluid Mech. 650, 5–55.CrossRefGoogle Scholar
Lucci, F., Ferrante, A. & Elghobashi, S. 2011 Is Stokes number an appropriate indicator for turbulence modulation by particles of Taylor length-scale size. Phys. Fluids 23, 025101.CrossRefGoogle Scholar
Maxey, M. R. 1987 The gravitational settling of aerosol particles in homogeneous turbulence and random flow fields. J. Fluid Mech. 174, 441–465.CrossRefGoogle Scholar
Moisy, F. & Jiménez, J. 2004 Geometry and clustering of intense structures in isotropic turbulence. J. Fluid Mech. 513, 111–133.CrossRefGoogle Scholar
Monchaux, R., Bourgoin, M. & Cartellier, A. 2010 Preferential concentration of heavy particles: A Voronoï analysis. Phys. Fluids 22, 103304.CrossRefGoogle Scholar
Monchaux, R., Bourgoin, M. & Cartellier, A. 2012 Analyzing preferential concentration and clustering of inertial particles in turbulence. Intl J. Multiphase Flow 40, 1–18.CrossRefGoogle Scholar
Mordant, N., Crawford, A. M. & Bodenschatz, E. 2004 Three-dimensional structure of the Lagrangian acceleration in turbulent flows. Phys. Rev. Lett. 93, 214501.CrossRefGoogle ScholarPubMed
Obligado, M., Teitelbaum, T., Cartellier, A., Mininni, P. & Bourgoin, M. 2014 Preferential concentration of heavy particles in turbulence. J. Turbul. 15 (5), 293–310.CrossRefGoogle Scholar
Qureshi, N. M., Arrieta, U., Baudet, C., Cartellier, A., Gagne, Y. & Bourgoin, M. 2008 Acceleration statistics of inertial particles in turbulent flow. Eur. Phys. J. B 66, 531–536.CrossRefGoogle Scholar
Qureshi, N. M., Bourgoin, M., Baudet, C., Cartellier, A. & Gagne, Y. 2007 Turbulent transport of material particles: an experimental study of finite-size effects. Phys. Rev. Lett. 99, 184502.CrossRefGoogle ScholarPubMed
She, Z.-S., Jackson, E. & Orszag, S. A. 1990 Intermittent vortex structures in homogeneous isotropic turbulence. Nature 344, 226–228.CrossRefGoogle Scholar
Squires, K. D. & Eaton, J. K. 1991 Preferential concentration of particles by turbulence. Phys. Fluids A 3 (5), 1169–1178.CrossRefGoogle Scholar
Sumbekova, S., Cartellier, A., Aliseda, A. & Bourgoin, M.2016 Preferential concentration of inertial sub-Kolmogorov particles. The roles of mass loading of particles, Stokes and Reynolds numbers, Phys. Rev. Fluids (submitted), arXiv:1607.01256.Google Scholar
Sundaram, S. & Collins, L. R. 1997 Collision statistics in an isotropic particle-laden turbulent suspension. Part 1. Direct numerical simulations. J. Fluid Mech. 335, 75–109.CrossRefGoogle Scholar
Ten Cate, A., Derksen, J. J., Portella, L. M. & Van Den Akker, H. E. 2004 Fully resolved simulations of colliding monodisperse spheres in forced isotropic turbulence. J. Fluid Mech. 519, 233–271.CrossRefGoogle Scholar
Uhlmann, M. 2005a An immersed boundary method with direct forcing for the simulation of particulate flows. J. Comput. Phys. 209 (2), 448–476.CrossRefGoogle Scholar
Uhlmann, M. 2005b An improved fluid-solid coupling method for DNS of particulate flow on a fixed mesh. In Proceedings of the 11th Workshop Two-Phase Flow Predictions (ed. Sommerfeld, M.). Universität Halle.Google Scholar
Uhlmann, M. 2006 Experience with DNS of particulate flow using a variant of the immersed boundary method. In Proceedings of ECCOMAS CFD 2006 (ed. Wesseling, P., Oñate, E. & Périaux, J.). ECCOMAS.Google Scholar
Uhlmann, M. 2008 Interface-resolved direct numerical simulation of vertical particulate channel flow in the turbulent regime. Phys. Fluids 20 (5), 053305.CrossRefGoogle Scholar
Uhlmann, M. & Doychev, T. 2014 Sedimentation of a dilute suspension of rigid spheres at intermediate Galileo numbers: the effect of clustering upon the particle motion. J. Fluid Mech. 752, 310–348.CrossRefGoogle Scholar
Uhlmann, M. & Dušek, J. 2014 The motion of a single heavy sphere in ambient fluid: a benchmark for interface-resolved particulate flow simulations with significant relative velocities. Intl J. Multiphase Flow 59, 221–243.CrossRefGoogle Scholar
Vedula, P. & Yeung, P. K. 1999 Similarity scaling of acceleration and pressure statistics in numerical simulations of isotropic turbulence. Phys. Fluids 11 (5), 1208–1220.CrossRefGoogle Scholar
Volk, R., Calzavarini, E., Lévêque, E. & Pinton, J.-F. 2011 Dynamics of inertial particles in a turbulent von Kármán flow. J. Fluid Mech. 668, 223–235.CrossRefGoogle Scholar
Volk, R., Calzavarini, E., Verhille, G., Lohse, D., Mordant, N., Pinton, J.-F. & Toschi, F. 2008 Acceleration of heavy and light particles in turbulence: comparison between experiments and direct numerical simulations. Physica D 237 (14–17), 2084–2089.CrossRefGoogle Scholar
Voth, G. A., la Porta, A., Crawford, A. M., Alexander, J. & Bodenschatz, E. 2002 Measurement of particle accelerations in fully developed turbulence. J. Fluid Mech. 469, 121–160.CrossRefGoogle Scholar
Wilczek, M., Daitche, A. & Friedrich, R. 2011 On the velocity distribution in homogeneous isotropic turbulence: correlations and deviations from Gaussianity. J. Fluid Mech. 676, 191–217.CrossRefGoogle Scholar
Wood, A. M., Hwang, W. & Eaton, J. K. 2005 Preferential concentration of particles in homogeneous and isotropic turbulence. Intl J. Multiphase Flow 31, 1220–1230.CrossRefGoogle Scholar
Yeo, K., Dong, S., Climent, E. & Maxey, M. R. 2010 Modulation of homogeneous turbulence seeded with finite size bubbles or particles. Intl J. Multiphase Flow 36 (3), 221–233.CrossRefGoogle Scholar
Yeung, P. K. & Pope, S. B. 1989 Lagrangian statistics from direct numerical simulations of isotropic turbulence. J. Fluid Mech. 207, 531–586.CrossRefGoogle Scholar
Yoshimoto, H. & Goto, S. 2007 Self-similar clustering of inertial particles in homogeneous turbulence. J. Fluid Mech. 577, 275–286.CrossRefGoogle Scholar
Zaichik, L. I. & Alipchenkov, V. M. 2003 Pair dispersion and preferential concentration of particles in isotropic turbulence. Phys. Fluids 15 (6), 1776–1787.CrossRefGoogle Scholar
Zaichik, L. I. & Alipchenkov, V. M. 2007 Refinement of the probability density function model for preferential concentration of aerosol particles in isotropic turbulence. Phys. Fluids 19 (11), 113308.CrossRefGoogle Scholar