Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-12-01T01:42:48.208Z Has data issue: false hasContentIssue false
  • English
  • Français

Closed-form solution for the edge vortex of a revolving plate

Published online by Cambridge University Press:  18 May 2017

Di Chen Open the ORCID record for Di Chen [Opens in a new window] ,
Dmitry Kolomenskiy Open the ORCID record for Dmitry Kolomenskiy [Opens in a new window]  and
Hao Liu Open the ORCID record for Hao Liu [Opens in a new window]
Di Chen
Affiliation:
School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiao Tong University, Shanghai 200240, People’s Republic of China Graduate School of Engineering, Chiba University, Chiba 263-8522, Japan Shanghai Jiao Tong University and Chiba University International Cooperative Research Center (SJTU-CU ICRC), Shanghai, People’s Republic of China
Dmitry Kolomenskiy*
Affiliation:
Graduate School of Engineering, Chiba University, Chiba 263-8522, Japan Center for Earth Information Science and Technology (CEIST), Japan Agency for Marine–Earth Science and Technology (JAMSTEC), Yokohama 236-0001, Japan
Hao Liu*
Affiliation:
Graduate School of Engineering, Chiba University, Chiba 263-8522, Japan Shanghai Jiao Tong University and Chiba University International Cooperative Research Center (SJTU-CU ICRC), Shanghai, People’s Republic of China
*
†Email addresses for correspondence: [email protected], [email protected]
†Email addresses for correspondence: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

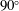Flapping and revolving wings can produce attached leading-edge vortices when the angle of attack is large. In this work, a low-order model is proposed for the edge vortices that develop on a revolving plate at $90^{\circ }$ angle of attack, which is the simplest limiting case, yet shows remarkable similarity with the generally known leading-edge vortices. The problem is solved analytically, providing short closed-form expressions for the circulation and the position of the vortex. The good agreement with the numerical solution of the Navier–Stokes equations suggests that, for the conditions examined, the vorticity production at the sharp edge and its subsequent three-dimensional transport are the main effects that shape the edge vortex.

JFM classification

Wakes/Jets: Separated flows Biological Fluid Dynamics: Swimming/flying Vortex Flows: Vortex dynamics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 821 , 25 June 2017 , pp. 200 - 218
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Birch, J. M. & Dickinson, M. H. 2001 Spanwise flow and the attachment of the leading-edge vortex on insect wings. Nature 412 (6848), 729–733.Google Scholar
Brown, C. E. & Michael, W. H. 1954 Effect of leading-edge separation on the lift of a delta wing. J. Aero. Sci. 21 (10), 690–694.Google Scholar
Carr, Z. R., DeVoria, A. C. & Ringuette, M. J. 2015 Aspect-ratio effects on rotating wings: circulation and forces. J. Fluid Mech. 767, 497–525.Google Scholar
Cortelezzi, L. 1995 On the unsteady separated flow past a semi-infinite plate: exact solution of the Brown and Michael model, scaling, and universality. Phys. Fluids 7 (3), 526–529.Google Scholar
Ellington, C. P., van den Berg, C., Willmott, A. P. & Thomas, A. L. R. 1996 Leading-edge vortices in insect flight. Nature 384 (6610), 626–630.Google Scholar
Garmann, D. J. & Visbal, M. R. 2014 Dynamics of revolving wings for various aspect ratios. J. Fluid Mech. 748, 932–956.Google Scholar
Garmann, D. J., Visbal, M. R. & Orkwis, P. D. 2013 Three-dimensional flow structure and aerodynamic loading on a revolving wing. Phys. Fluids 25 (3), 034101.Google Scholar
Harbig, R. R., Sheridan, J. & Thompson, M. C. 2013 Reynolds number and aspect ratio effects on the leading-edge vortex for rotating insect wing planforms. J. Fluid Mech. 717, 166–192.Google Scholar
Kolomenskiy, D., Elimelech, Y. & Schneider, K. 2014 Leading-edge vortex shedding from rotating wings. Fluid Dyn. Res. 46, 031421.Google Scholar
Kruyt, J. W., van Heijst, G. F., Altshuler, D. L. & Lentink, D. 2015 Power reduction and the radial limit of stall delay in revolving wings of different aspect ratio. J. R. Soc. Interface 12 (105), 20150051.Google Scholar
Lentink, D. & Dickinson, M. H. 2009 Rotational accelerations stabilize leading edge vortices on revolving fly wings. J. Expl Biol. 212, 2705–2719.Google Scholar
Limacher, E., Morton, C. & Wood, D. 2016 On the trajectory of leading-edge vortices under the influence of Coriolis acceleration. J. Fluid Mech. 800, R1.Google Scholar
Liu, H., Ellington, C. P., Kawachi, K., van den Berg, C. & Willmott, A. P. 1998 A computational fluid dynamic study of hawkmoth hovering. J. Expl Biol. 201 (4), 461–477.Google Scholar
Maxworthy, T. 1979 Experiments on the Weis–Fogh mechanism of lift generation by insects in hovering flight. Part 1. Dynamics of the ‘fling’. J. Fluid Mech. 93 (1), 47–63.Google Scholar
Maxworthy, T. 2007 The formation and maintenance of a leading-edge vortex during the forward motion of an animal wing. J. Fluid Mech. 587, 471–475.Google Scholar
Michelin, S. & Llewellyn Smith, S. G. 2009 An unsteady point vortex method for coupled fluid–solid problems. Theor. Comput. Fluid Dyn. 23 (2), 127–153.Google Scholar
Phillips, N., Knowles, K. & Bomphrey, R. J. 2017 Petiolate wings: effects on the leading-edge vortex in flapping flight. Interface Focus 7 (1), 20160084.Google Scholar
Usherwood, J. R. & Ellington, C. P. 2002 The aerodynamics of revolving wings II. Propeller force coefficients from mayfly to quail. J. Expl Biol. 205 (11), 1565–1576.Google Scholar
Wang, C. & Eldredge, J. D. 2013 Low-order phenomenological modeling of leading-edge vortex formation. Theor. Comput. Fluid Dyn. 27 (5), 577–598.Google Scholar
Wojcik, C. J. & Buchholz, J. H. J. 2014 Vorticity transport in the leading-edge vortex on a rotating blade. J. Fluid Mech. 743, 249–261.Google Scholar
Supplementary material: File

Chen supplementary material

Chen supplementary material 1

Download Chen supplementary material(File)
File 7.3 KB