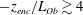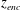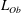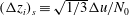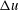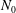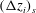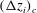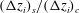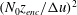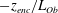1 Introduction
Entrainment, the process by which air from the free atmosphere is incorporated and mixed into the boundary-layer interior, is crucial for the structure and evolution of planetary boundary layers. Entrainment is important for cloud formation and desiccation at the boundary-layer top, for the evolution of mixed-layer properties in the interior and for surface processes. However, characterizing entrainment remains a challenge despite continuing efforts. On one hand, it is difficult to obtain accurate data at the required small scales. On the other hand, entrainment often compounds turbulent mixing in a stably stratified environment with other complex phenomena such as clouds and wind shear (Stull Reference Stull and Stull1988; Garratt Reference Garratt1992; Mellado Reference Mellado2017). In this paper, we study the effect of wind shear on entrainment in a cloud-free convective boundary layer (CBL).
The effect of wind shear on entrainment in CBLs has been studied by means of atmospheric measurements, laboratory experiments and numerical simulations (see reviews in Conzemius & Fedorovich (Reference Conzemius and Fedorovich2006a ) and Fedorovich & Conzemius (Reference Fedorovich and Conzemius2008) and references therein). These studies have shown that wind shear generally enhances entrainment, which thickens the entrainment zone and increases the growth rate of the CBL. The entrainment zone is defined as the region of negative buoyancy flux at the boundary-layer top. The main cause for this enhancement is the shear-generated turbulence in the entrainment zone, and not the vertical transport of shear-generated turbulence in the surface layer. The shear in the surface layer affects entrainment mainly indirectly by slowing the flow in the CBL interior, which leads to the formation of a localized shear layer at the CBL top. This indirect effect is even found in the absence of convection, when turbulence is solely mechanically driven (Jonker et al. Reference Jonker, van Reeuwijk, Sullivan and Patton2013). Consequently, local scales in the entrainment zone become more important in sheared CBLs than in shear-free CBLs, and the boundary-layer depth and the associated convective scales are insufficient to characterize the system (Conzemius & Fedorovich Reference Conzemius and Fedorovich2006b , Reference Conzemius and Fedorovich2007; Kim et al. Reference Kim, Park, Pino and Vilà-Guerau De Arellano2006). Nonetheless, the quantification of the shear enhancement of entrainment and of its dependence on the environmental conditions remains difficult. In the work here presented, we use a configuration of reduced complexity to better understand and characterize the vertical structure of the entrainment zone, and we use this new characterization to quantify the dependence of entrainment-zone properties on the surface and free-atmosphere conditions.
We consider a zero-pressure-gradient turbulent boundary layer that is forced by a constant surface buoyancy flux and that grows into a linearly stratified atmosphere. As we will show, such a configuration is representative of a barotropic CBL over land. Mixing and entrainment in a stably stratified environment have often been studied in idealized configurations where the turbulence is forced by a grid or by an imposed mean shear (e.g. Fernando Reference Fernando1991; Strang & Fernando Reference Strang and Fernando2001; Peltier & Caulfield Reference Peltier and Caulfield2003; Chung & Matheou Reference Chung and Matheou2012; and references therein). From these studies, we have learned about various mixing mechanisms and entrainment-rate laws depending on the stratification conditions. However, it remains difficult to extend these results to the entrainment zone of CBLs. For instance, these previous studies indicate that the buoyancy Reynolds number should be of the order of 100 for large patches of turbulence to be sustained (Smyth & Moum Reference Smyth and Moum2000a ; Portwood et al. Reference Portwood, de Bruyn Kops, Taylor, Salehipour and Caulfield2016), whereas buoyancy Reynolds numbers of the order of 10 are sufficient in the entrainment zone of CBLs (Garcia & Mellado Reference Garcia and Mellado2014). The reason for this difference is that large-scale updraughts in the CBL continuously transport turbulence into the entrainment zone. Besides, turbulence in the CBL has its distinct properties, such as the large-scale organization of the flow in convective rolls and the possible interaction between entrainment and near-surface dynamics (LeMone Reference Lemone1973; Moeng & Sullivan Reference Moeng and Sullivan1994; van de Boer et al. Reference van de Boer, Moene, Graf, Schüttemeyer and Simmer2014; Salesky, Chamecki & Bou-Zeid Reference Salesky, Chamecki and Bou-Zeid2017). Configurations of intermediate complexity such as the one considered here provide a closer representation of planetary boundary layers and can help to transfer results from studies of more idealized configurations, such as stratified shear layers and homogeneous stratified shear turbulence, to planetary boundary layers.
Because of the relevance of the local shear in the entrainment zone, understanding the vertical structure of the entrainment zone is crucial to understand shear effects on entrainment. In shear-free CBLs, Garcia & Mellado (Reference Garcia and Mellado2014) have introduced a two-layer structure to describe the entrainment zone. The lower sublayer is characterized by global scales, namely, by a length scale proportional to the CBL depth and by the convective scales that characterize the variances in the CBL interior. The upper sublayer acts as a transition layer between the turbulent region below and the non-turbulent stably stratified region above, and is characterized by local scales. As the CBL broadens, the upper sublayer becomes thinner compared to the lower sublayer. This two-layer structure rationalizes the observation that the entrainment-zone thickness deviates from a constant fraction of the CBL depth as the CBL grows (Deardorff, Willis & Stochton Reference Deardorff, Willis and Stochton1980; Sullivan et al. Reference Sullivan, Moeng, Stevens, Lenschow and Mayor1998), and that the variance correlates with the local gradients and not with the convective scales that characterize the CBL interior (Deardorff Reference Deardorff1974; Sorbjan Reference Sorbjan2005). This two-layer structure also helps explain the observed dependence on weak and strong stratification regimes of the minimum buoyancy flux, and of the relationship between the mean entrainment velocity and the convective Richardson number. In this work, we show that the entrainment zone in sheared CBLs is also better described as a two-layer structure.
One last goal of the work presented here is to quantify the dependence of entrainment-zone properties on environmental conditions, which is particularly important for sheared CBLs because, as indicated above, these properties partly define the evolution of global CBL properties. Previous studies have identified major sensitivities of entrainment-zone properties to changes in environmental conditions. For instance, Pino & Vilà-Guerau De Arellano (Reference Pino and Vilà-Guerau De Arellano2008) showed that entrainment generally increases with the wind velocity in the free atmosphere. Conzemius & Fedorovich (Reference Conzemius and Fedorovich2006a ) found that increasing the free-atmosphere stratification or decreasing the surface buoyancy flux enhances shear effects, because a slower CBL growth permits the accumulation of more shear in the entrainment zone. Mahrt & Lenschow (Reference Mahrt and Lenschow1976) and Kim, Park & Moeng (Reference Kim, Park and Moeng2003) observed that gradient and flux Richardson numbers in the entrainment zone approach constant values in the range 0.25–0.3 as shear increases, which indicates a balance between shear production of turbulence kinetic energy (TKE), buoyancy destruction and viscous dissipation. This condition is accompanied by patches of Kelvin–Helmholtz-like billows, which are induced by convective thermals impinging into the inversion and reducing locally the gradient Richardson number (Kim et al. Reference Kim, Park and Moeng2003). The quantification of these sensitivities, however, remains elusive. In this paper, we provide explicit scaling laws in terms of the surface and free-atmosphere conditions. Based on these scaling laws, we identify the conditions for which shear effects become relevant, and for which shear effects become of order one. In contrast to previous work, the scaling laws proposed here do not have a singularity at a finite wind strength.
One curious aspect of wind-shear effects on entrainment is that, for weak shear conditions and during the early state of the CBL development, entrainment slightly decreases with respect to the shear-free CBL (Conzemius & Fedorovich Reference Conzemius and Fedorovich2006a ; Pino & Vilà-Guerau De Arellano Reference Pino and Vilà-Guerau De Arellano2008). Such a reduction has been associated with the blockage of turbulence propagation near a turbulent/non-turbulent interface (Hunt & Durbin Reference Hunt and Durbin1999; Fedorovich & Thäter Reference Fedorovich and Thäter2001), and with the enhancement of the energy drain from the CBL top by gravity-wave radiation into the free atmosphere (Schröter Reference Schröter2018). It remains unclear, however, how much this phenomenon depends on the initial conditions and on the different CBL regimes. Systematic studies of sheared CBLs can also help to clarify this aspect.
We note that one key to better quantify entrainment is to obtain accurate data at the required small scales, which are of the order of tens of metres. Typical grid spacings in large-eddy simulations are also of the order of 10 m or more, and hence simulated properties can be strongly affected by the subgrid-scale models and numerical artefacts, as illustrated by the order-of-one intra-model variability of the minimum buoyancy flux in the intercomparison study of Fedorovich et al. (Reference Fedorovich, Conzemius, Esau, Chow, Lewellen, Moeng, Sullivan, Pino and Vilà-Guerau De Arellano2004a ). To reduce this uncertainty, we use direct numerical simulation (DNS) and assess the dependence of the results on the Reynolds number.
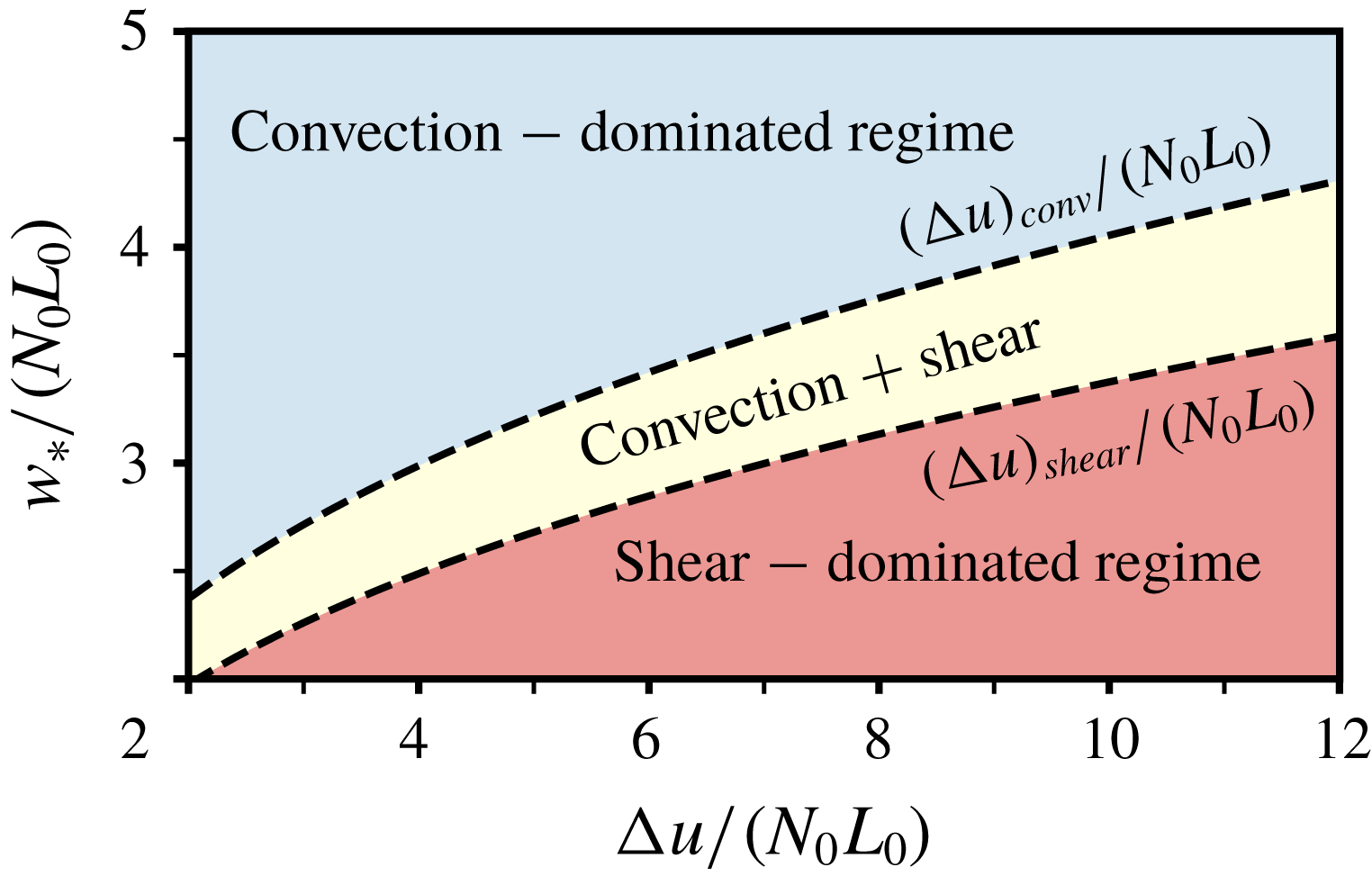
The structure of the paper is as follows. After defining the problem in § 2, we discuss in § 3 wind-shear effects on buoyancy and velocity properties, identifying the conditions at which these effects become significant. In § 4, we characterize the two-layer structure of the entrainment zone. The local scales identified in this section are then used in § 5 to provide scaling laws that express the dependence of entrainment-zone properties on the surface and free-atmosphere conditions, and on the state of development of the CBL. In § 6, we use the results to define a convection-dominated regime, where shear effects are negligible, and a shear-dominated regime, where shear effects are of the order of one. We finally summarize these results and draw conclusions in § 7.
2 Problem definition
We consider a cloud-free CBL that develops over a flat, aerodynamically smooth wall and penetrates into a free atmosphere with constant buoyancy gradient,
![]() $N_{0}^{2}$
, where
$N_{0}^{2}$
, where
![]() $N_{0}$
is the Brunt–Väisälä frequency (see figure 1). Convection is forced by a constant and homogeneous surface buoyancy flux,
$N_{0}$
is the Brunt–Väisälä frequency (see figure 1). Convection is forced by a constant and homogeneous surface buoyancy flux,
![]() $B_{0}$
. We consider barotropic conditions, i.e. the wind strength in the free atmosphere,
$B_{0}$
. We consider barotropic conditions, i.e. the wind strength in the free atmosphere,
![]() $U_{0}$
, is constant with height (Fedorovich & Conzemius Reference Fedorovich and Conzemius2008; Pino & Vilà-Guerau De Arellano Reference Pino and Vilà-Guerau De Arellano2008). This configuration is representative of midday conditions over land. In addition, we consider the limit of zero Coriolis parameter, which implies that the mean pressure gradient associated with the geostrophic balance is zero. Results show that our simulations reproduce the main features of barotropic CBLs in middle latitudes, and the limit of zero Coriolis parameter provides a reference case to systematically study Coriolis effects. The resulting configuration is a temporally evolving zero-pressure-gradient boundary layer that is convectively forced at the surface. Because of the stable stratification in the free atmosphere, the boundary layer develops in a quasi-steady regime, in which CBL properties evolve on time scales much larger than the eddy turnover time of the large, energy-containing motions. We focus on this quasi-steady regime.
$U_{0}$
, is constant with height (Fedorovich & Conzemius Reference Fedorovich and Conzemius2008; Pino & Vilà-Guerau De Arellano Reference Pino and Vilà-Guerau De Arellano2008). This configuration is representative of midday conditions over land. In addition, we consider the limit of zero Coriolis parameter, which implies that the mean pressure gradient associated with the geostrophic balance is zero. Results show that our simulations reproduce the main features of barotropic CBLs in middle latitudes, and the limit of zero Coriolis parameter provides a reference case to systematically study Coriolis effects. The resulting configuration is a temporally evolving zero-pressure-gradient boundary layer that is convectively forced at the surface. Because of the stable stratification in the free atmosphere, the boundary layer develops in a quasi-steady regime, in which CBL properties evolve on time scales much larger than the eddy turnover time of the large, energy-containing motions. We focus on this quasi-steady regime.
2.1 Governing equations
We solve the conservation equations for mass, momentum, and energy in the Boussinesq approximation:

Figure 1. Sketch of the barotropic CBL considered in this analysis. The vertical white bars indicate different definitions of the CBL depth, namely, from left to right, the encroachment length scale,
![]() $z_{enc}$
, the flux-based height,
$z_{enc}$
, the flux-based height,
![]() $z_{i,f}$
, and the gradient-based height,
$z_{i,f}$
, and the gradient-based height,
![]() $z_{i,g}$
. The background is a cross-section of the logarithm of the magnitude of the buoyancy gradient from case
$z_{i,g}$
. The background is a cross-section of the logarithm of the magnitude of the buoyancy gradient from case
![]() $Fr_{0}=20$
and
$Fr_{0}=20$
and
![]() $Re_{0}=25$
of table 1 at
$Re_{0}=25$
of table 1 at
![]() $z_{enc}/L_{0}\simeq 15$
. (The image only shows the lower
$z_{enc}/L_{0}\simeq 15$
. (The image only shows the lower
![]() $40\,\%$
of the vertical domain.)
$40\,\%$
of the vertical domain.)
Impermeable, no-slip and impermeable, free-slip boundary conditions are applied, respectively, at the bottom and at the top of the domain. Neumann boundary conditions are used for the buoyancy at the bottom,
![]() $\unicode[STIX]{x2202}_{z}b=-B_{0}/\unicode[STIX]{x1D705}_{b}$
, and at the top,
$\unicode[STIX]{x2202}_{z}b=-B_{0}/\unicode[STIX]{x1D705}_{b}$
, and at the top,
![]() $\unicode[STIX]{x2202}_{z}b=N_{0}^{2}$
, to maintain fixed constant fluxes. Periodicity is applied at the lateral boundaries. A linear relaxation term acts on the velocity and buoyancy fields inside a sponge layer occupying the upper 15 %–20 % of the computational domain. The reference values of this relaxation term are the initial conditions. The proportionality coefficient of the relaxation term increases quadratically with the distance from the inner limit of the sponge layer, from zero at the inner limit to
$\unicode[STIX]{x2202}_{z}b=N_{0}^{2}$
, to maintain fixed constant fluxes. Periodicity is applied at the lateral boundaries. A linear relaxation term acts on the velocity and buoyancy fields inside a sponge layer occupying the upper 15 %–20 % of the computational domain. The reference values of this relaxation term are the initial conditions. The proportionality coefficient of the relaxation term increases quadratically with the distance from the inner limit of the sponge layer, from zero at the inner limit to
![]() $N_{0}/(2\unicode[STIX]{x03C0})$
at the outer limit (which coincides with the top of the computational domain).
$N_{0}/(2\unicode[STIX]{x03C0})$
at the outer limit (which coincides with the top of the computational domain).
The initial buoyancy field is defined as
where
![]() $b_{ics}(x_{1},x_{2})=(B_{0}/\unicode[STIX]{x1D705}_{b}+N_{0}^{2})\unicode[STIX]{x1D6FF}_{ics}(x_{1},x_{2})$
is the surface buoyancy and
$b_{ics}(x_{1},x_{2})=(B_{0}/\unicode[STIX]{x1D705}_{b}+N_{0}^{2})\unicode[STIX]{x1D6FF}_{ics}(x_{1},x_{2})$
is the surface buoyancy and
![]() $\unicode[STIX]{x1D6FF}_{ics}$
is the local gradient thickness (Mellado, van Heerwaarden & Garcia Reference Mellado, van Heerwaarden and Garcia2016). A broadband field is constructed by specifying
$\unicode[STIX]{x1D6FF}_{ics}$
is the local gradient thickness (Mellado, van Heerwaarden & Garcia Reference Mellado, van Heerwaarden and Garcia2016). A broadband field is constructed by specifying
![]() $\unicode[STIX]{x1D6FF}_{ics}(x_{1},x_{2})=\unicode[STIX]{x1D6FF}_{0}[1+\unicode[STIX]{x1D709}(x_{1},x_{2})]$
, with the parameter
$\unicode[STIX]{x1D6FF}_{ics}(x_{1},x_{2})=\unicode[STIX]{x1D6FF}_{0}[1+\unicode[STIX]{x1D709}(x_{1},x_{2})]$
, with the parameter
![]() $\unicode[STIX]{x1D6FF}_{0}$
to be given. The random field
$\unicode[STIX]{x1D6FF}_{0}$
to be given. The random field
![]() $\unicode[STIX]{x1D709}(x_{1},x_{2})$
has a Gaussian power spectral density centred at a spatial frequency
$\unicode[STIX]{x1D709}(x_{1},x_{2})$
has a Gaussian power spectral density centred at a spatial frequency
![]() $\unicode[STIX]{x1D706}_{0}^{-1}=(4\unicode[STIX]{x1D6FF}_{0})^{-1}$
and with a standard deviation
$\unicode[STIX]{x1D706}_{0}^{-1}=(4\unicode[STIX]{x1D6FF}_{0})^{-1}$
and with a standard deviation
![]() $(6\unicode[STIX]{x1D706}_{0})^{-1}$
, so that there is practically no energy with spatial frequencies below
$(6\unicode[STIX]{x1D706}_{0})^{-1}$
, so that there is practically no energy with spatial frequencies below
![]() $(2\unicode[STIX]{x1D706}_{0})^{-1}$
. The phase of
$(2\unicode[STIX]{x1D706}_{0})^{-1}$
. The phase of
![]() $\unicode[STIX]{x1D709}$
is random, its mean value is zero and the root-mean-square (r.m.s.) is
$\unicode[STIX]{x1D709}$
is random, its mean value is zero and the root-mean-square (r.m.s.) is
![]() $\unicode[STIX]{x1D709}_{rms}=0.1$
. The initial velocity field is imposed as
$\unicode[STIX]{x1D709}_{rms}=0.1$
. The initial velocity field is imposed as
where
![]() $\boldsymbol{i}=(1,0,0)$
. Such a function provides the no-slip boundary condition at the surface and a height-constant velocity in the streamwise direction in the bulk of the domain.
$\boldsymbol{i}=(1,0,0)$
. Such a function provides the no-slip boundary condition at the surface and a height-constant velocity in the streamwise direction in the bulk of the domain.
A finite difference method using Cartesian coordinates and a structured grid is employed to solve the governing equations. The discretization of the equations is carried out by sixth-order spectral-like compact schemes for the spatial derivatives (Lele Reference Lele1992) along with a low-storage fourth-order Runge–Kutta scheme to advance in time (Carpenter & Kennedy Reference Carpenter and Kennedy1994). For the compact schemes used in this study, approximately four points per wavelength provide
![]() $99\,\%$
accuracy in the transfer function of the derivative operator. For comparison, second-order central schemes need approximately eight points per wavelength to reach
$99\,\%$
accuracy in the transfer function of the derivative operator. For comparison, second-order central schemes need approximately eight points per wavelength to reach
![]() $90\,\%$
accuracy, which is the motivation to employ compact schemes despite being computationally more demanding (Lele Reference Lele1992). The pressure-Poisson equation is solved using a Fourier decomposition along the horizontal directions, which results in a set of second-order differential equations along the vertical coordinate (Mellado & Ansorge Reference Mellado and Ansorge2012).
$90\,\%$
accuracy, which is the motivation to employ compact schemes despite being computationally more demanding (Lele Reference Lele1992). The pressure-Poisson equation is solved using a Fourier decomposition along the horizontal directions, which results in a set of second-order differential equations along the vertical coordinate (Mellado & Ansorge Reference Mellado and Ansorge2012).
2.2 Dimensional analysis
The sheared CBL described in the previous section is completely governed by the control parameters
![]() $\{\unicode[STIX]{x1D708},\unicode[STIX]{x1D705}_{b},B_{0},N_{0},U_{0}\}$
once the turbulent flow has sufficiently forgotten the initial conditions. Hence, three non-dimensional parameters are sufficient to characterize the system. In this work, we take the shear-free limit
$\{\unicode[STIX]{x1D708},\unicode[STIX]{x1D705}_{b},B_{0},N_{0},U_{0}\}$
once the turbulent flow has sufficiently forgotten the initial conditions. Hence, three non-dimensional parameters are sufficient to characterize the system. In this work, we take the shear-free limit
![]() $U_{0}=0$
as reference and study how entrainment-zone properties change as we gradually increase the wind velocity. Hence, we choose
$U_{0}=0$
as reference and study how entrainment-zone properties change as we gradually increase the wind velocity. Hence, we choose
![]() $N_{0}$
and
$N_{0}$
and
![]() $B_{0}$
to non-dimensionalize the problem, which yields
$B_{0}$
to non-dimensionalize the problem, which yields
![]() $N_{0}^{-1}$
as the reference time scale,
$N_{0}^{-1}$
as the reference time scale,
as the reference length scale, and
![]() $N_{0}L_{0}=(B_{0}/N_{0})^{1/2}$
as the reference velocity scale. (Henceforth, the symbol
$N_{0}L_{0}=(B_{0}/N_{0})^{1/2}$
as the reference velocity scale. (Henceforth, the symbol
![]() $\equiv$
indicates a definition.) The characteristic length scale
$\equiv$
indicates a definition.) The characteristic length scale
![]() $L_{0}$
will be referred to as the reference Ozmidov length. This scale provides a reference value of the Ozmidov length
$L_{0}$
will be referred to as the reference Ozmidov length. This scale provides a reference value of the Ozmidov length
in the entrainment zone, since the viscous dissipation rate
![]() $\unicode[STIX]{x1D700}$
in shear-free CBLs is an order-of-one fraction of the surface buoyancy flux
$\unicode[STIX]{x1D700}$
in shear-free CBLs is an order-of-one fraction of the surface buoyancy flux
![]() $B_{0}$
(Fedorovich, Conzemius & Mironov Reference Fedorovich, Conzemius and Mironov2004b
), and the mean buoyancy gradient
$B_{0}$
(Fedorovich, Conzemius & Mironov Reference Fedorovich, Conzemius and Mironov2004b
), and the mean buoyancy gradient
![]() $N^{2}$
is partly characterized by
$N^{2}$
is partly characterized by
![]() $N_{0}^{2}$
(Garcia & Mellado Reference Garcia and Mellado2014). The Ozmidov length represents the size of the largest motions unaffected by a background stratification
$N_{0}^{2}$
(Garcia & Mellado Reference Garcia and Mellado2014). The Ozmidov length represents the size of the largest motions unaffected by a background stratification
![]() $N^{2}$
in a turbulent field characterized by a viscous dissipation rate
$N^{2}$
in a turbulent field characterized by a viscous dissipation rate
![]() $\unicode[STIX]{x1D700}$
(Dougherty Reference Dougherty1961; Ozmidov Reference Ozmidov1965). Garcia & Mellado (Reference Garcia and Mellado2014) and Mellado, Puche & van Heerwaarden (Reference Mellado, Puche and van Heerwaarden2017) have shown that, in shear-free CBLs,
$\unicode[STIX]{x1D700}$
(Dougherty Reference Dougherty1961; Ozmidov Reference Ozmidov1965). Garcia & Mellado (Reference Garcia and Mellado2014) and Mellado, Puche & van Heerwaarden (Reference Mellado, Puche and van Heerwaarden2017) have shown that, in shear-free CBLs,
![]() $L_{0}$
helps characterize the main properties in the upper region of the entrainment zone, such as the mean gradients and variances of temperature and specific humidity. We will show that
$L_{0}$
helps characterize the main properties in the upper region of the entrainment zone, such as the mean gradients and variances of temperature and specific humidity. We will show that
![]() $L_{0}$
is also a useful parameter to characterize the entrainment zone in the sheared CBLs considered in this study.
$L_{0}$
is also a useful parameter to characterize the entrainment zone in the sheared CBLs considered in this study.
The shear-free limit is fully characterized by a reference buoyancy Reynolds number
and the Prandtl number
![]() $Pr\equiv \unicode[STIX]{x1D708}/\unicode[STIX]{x1D705}_{b}$
. The parameter
$Pr\equiv \unicode[STIX]{x1D708}/\unicode[STIX]{x1D705}_{b}$
. The parameter
![]() $Re_{0}$
provides a reference value of the buoyancy Reynolds number
$Re_{0}$
provides a reference value of the buoyancy Reynolds number
in the lower part of the entrainment zone, since
![]() $\unicode[STIX]{x1D700}\sim B_{0}$
and
$\unicode[STIX]{x1D700}\sim B_{0}$
and
![]() $N\sim N_{0}$
in shear-free CBLs, as explained before. A buoyancy Reynolds number is often used in the study of the interaction between turbulence and stable stratification (see e.g. Smyth & Moum Reference Smyth and Moum2000a
; Hebert & de Bruyn Kops Reference Hebert and de Bruyn Kops2006; Chung & Matheou Reference Chung and Matheou2012; Portwood et al.
Reference Portwood, de Bruyn Kops, Taylor, Salehipour and Caulfield2016). As explained in the introduction, the work presented here helps ascertain to what extent results from those previous studies apply to the entrainment zone of sheared CBLs.
$N\sim N_{0}$
in shear-free CBLs, as explained before. A buoyancy Reynolds number is often used in the study of the interaction between turbulence and stable stratification (see e.g. Smyth & Moum Reference Smyth and Moum2000a
; Hebert & de Bruyn Kops Reference Hebert and de Bruyn Kops2006; Chung & Matheou Reference Chung and Matheou2012; Portwood et al.
Reference Portwood, de Bruyn Kops, Taylor, Salehipour and Caulfield2016). As explained in the introduction, the work presented here helps ascertain to what extent results from those previous studies apply to the entrainment zone of sheared CBLs.
To characterize wind-shear effects, we use the reference Froude number
as the third non-dimensional parameter. The denominator is the velocity scale that stems from the buoyancy acceleration
![]() $N_{0}^{2}L_{0}$
associated with a vertical displacement
$N_{0}^{2}L_{0}$
associated with a vertical displacement
![]() $L_{0}$
in an environment with a buoyancy stratification
$L_{0}$
in an environment with a buoyancy stratification
![]() $N_{0}^{2}$
. The last equality follows from the definition of
$N_{0}^{2}$
. The last equality follows from the definition of
![]() $L_{0}$
and indicates that
$L_{0}$
and indicates that
![]() $Fr_{0}$
can be interpreted as the ratio between the wind velocity in the free atmosphere and the velocity scale associated with motions of size
$Fr_{0}$
can be interpreted as the ratio between the wind velocity in the free atmosphere and the velocity scale associated with motions of size
![]() $L_{0}$
in a turbulent cascade characterized by an energy transfer rate
$L_{0}$
in a turbulent cascade characterized by an energy transfer rate
![]() $B_{0}$
, as is the case in shear-free CBLs.
$B_{0}$
, as is the case in shear-free CBLs.
Owing to statistical homogeneity in the horizontal directions, statistical properties are only functions of two independent variables, namely, height and time
![]() $\{z,t\}$
. Following previous work in shear-free CBLs growing into linearly stratified atmospheres (Garcia & Mellado Reference Garcia and Mellado2014; van Heerwaarden & Mellado Reference van Heerwaarden and Mellado2016; Mellado et al.
Reference Mellado, van Heerwaarden and Garcia2016), we use the non-dimensionalized form of these variables
$\{z,t\}$
. Following previous work in shear-free CBLs growing into linearly stratified atmospheres (Garcia & Mellado Reference Garcia and Mellado2014; van Heerwaarden & Mellado Reference van Heerwaarden and Mellado2016; Mellado et al.
Reference Mellado, van Heerwaarden and Garcia2016), we use the non-dimensionalized form of these variables
![]() $\{z/z_{enc},z_{enc}/L_{0}\}$
. The variable
$\{z/z_{enc},z_{enc}/L_{0}\}$
. The variable
![]() $z_{enc}$
is the encroachment length scale defined as
$z_{enc}$
is the encroachment length scale defined as
where
![]() $z_{\infty }$
is located far enough into the non-turbulent free atmosphere for the integral to become approximately independent of
$z_{\infty }$
is located far enough into the non-turbulent free atmosphere for the integral to become approximately independent of
![]() $z_{\infty }$
. Angle brackets denote averaging along horizontal planes. The integral analysis of the buoyancy equation (2.1c
) yields
$z_{\infty }$
. Angle brackets denote averaging along horizontal planes. The integral analysis of the buoyancy equation (2.1c
) yields
where
![]() $t_{0}$
is a constant of integration, so that
$t_{0}$
is a constant of integration, so that
![]() $z_{enc}$
can be easily calculated at any time. The reason to use
$z_{enc}$
can be easily calculated at any time. The reason to use
![]() $z_{enc}$
instead of time as independent variable is that the encroachment length scale provides a measure of the shear-free CBL depth (Carson & Smith Reference Carson and Smith1975), and it can be calculated from the mean buoyancy profile according to (2.9), which makes it convenient for the interpretation of results. We will show that
$z_{enc}$
instead of time as independent variable is that the encroachment length scale provides a measure of the shear-free CBL depth (Carson & Smith Reference Carson and Smith1975), and it can be calculated from the mean buoyancy profile according to (2.9), which makes it convenient for the interpretation of results. We will show that
![]() $z_{enc}$
also provides a relevant depth measure for the sheared CBLs considered in this study.
$z_{enc}$
also provides a relevant depth measure for the sheared CBLs considered in this study.
The sheared CBL can also be partly characterized by the stability parameter defined as the ratio between the CBL depth and the Obukhov length (Stull Reference Stull and Stull1988). The Obukhov length is defined as
where
![]() $\unicode[STIX]{x1D705}\simeq 0.41$
is the von Kármán constant,
$\unicode[STIX]{x1D705}\simeq 0.41$
is the von Kármán constant,
is the friction velocity and
is a convective velocity scale (Deardorff Reference Deardorff1970). Very large values of
![]() $-z_{enc}/L_{Ob}$
correspond to nearly shear-free CBLs, and very small values correspond to nearly neutral, shear-driven boundary layers. When studying entrainment-zone properties, however, the stability parameter alone is not sufficient as an independent variable, and alternative options have been proposed, such as a Richardson number (see Conzemius & Fedorovich Reference Conzemius and Fedorovich2006b
; Pino & Vilà-Guerau De Arellano Reference Pino and Vilà-Guerau De Arellano2008; and references therein). We will discuss these alternative variables in § 6.
$-z_{enc}/L_{Ob}$
correspond to nearly shear-free CBLs, and very small values correspond to nearly neutral, shear-driven boundary layers. When studying entrainment-zone properties, however, the stability parameter alone is not sufficient as an independent variable, and alternative options have been proposed, such as a Richardson number (see Conzemius & Fedorovich Reference Conzemius and Fedorovich2006b
; Pino & Vilà-Guerau De Arellano Reference Pino and Vilà-Guerau De Arellano2008; and references therein). We will discuss these alternative variables in § 6.
2.3 Parameter space and description of simulations
For typical midday conditions,
![]() $N_{0}\simeq (0.6{-}1.8)\times 10^{-2}~\text{s}^{-1}$
,
$N_{0}\simeq (0.6{-}1.8)\times 10^{-2}~\text{s}^{-1}$
,
![]() $B_{0}\simeq (0.3{-}1.0)\times 10^{-2}~\text{m}^{2}~\text{s}^{-3}$
and
$B_{0}\simeq (0.3{-}1.0)\times 10^{-2}~\text{m}^{2}~\text{s}^{-3}$
and
![]() $z_{enc}\simeq 500{-}2000~\text{m}$
, one finds
$z_{enc}\simeq 500{-}2000~\text{m}$
, one finds
![]() $L_{0}\simeq 20{-}200~\text{m}$
and states of development in the range
$L_{0}\simeq 20{-}200~\text{m}$
and states of development in the range
![]() $z_{enc}/L_{0}\simeq 5{-}50$
. For these conditions and wind velocities in the interval
$z_{enc}/L_{0}\simeq 5{-}50$
. For these conditions and wind velocities in the interval
![]() $U_{0}=0{-}15~\text{m}~\text{s}^{-1}$
, the reference Froude number is in the range
$U_{0}=0{-}15~\text{m}~\text{s}^{-1}$
, the reference Froude number is in the range
![]() $Fr_{0}\simeq 0{-}35$
. Using
$Fr_{0}\simeq 0{-}35$
. Using
![]() $\unicode[STIX]{x1D705}_{b}=2.1\times 10^{-5}~\text{m}^{2}~\text{s}^{-1}$
and
$\unicode[STIX]{x1D705}_{b}=2.1\times 10^{-5}~\text{m}^{2}~\text{s}^{-1}$
and
![]() $\unicode[STIX]{x1D708}=1.5\times 10^{-5}~\text{m}^{2}~\text{s}^{-1}$
, one further obtains
$\unicode[STIX]{x1D708}=1.5\times 10^{-5}~\text{m}^{2}~\text{s}^{-1}$
, one further obtains
![]() $Re_{0}\simeq 6\times 10^{5}$
to
$Re_{0}\simeq 6\times 10^{5}$
to
![]() $2\times 10^{7}$
and
$2\times 10^{7}$
and
![]() $Pr\simeq 0.7$
.
$Pr\simeq 0.7$
.
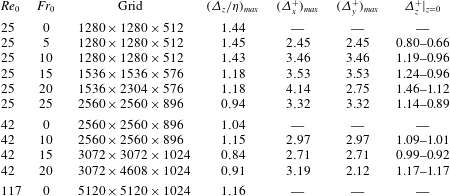
Table 1. Simulation properties. Columns 3–8 provide data at the final time of the simulations, and columns 9–11 show the variation between
![]() $z_{enc}/L_{0}=15$
and the final time of the simulations. Here
$z_{enc}/L_{0}=15$
and the final time of the simulations. Here
![]() $Re_{0}$
is the reference buoyancy Reynolds number defined by (2.6);
$Re_{0}$
is the reference buoyancy Reynolds number defined by (2.6);
![]() $Fr_{0}$
is the reference Froude number defined by (2.8);
$Fr_{0}$
is the reference Froude number defined by (2.8);
![]() $z_{enc}$
is the encroachment length defined by (2.9); and
$z_{enc}$
is the encroachment length defined by (2.9); and
![]() $L_{0}$
is the reference Ozmidov length defined by (2.4). The convective Reynolds number is defined as
$L_{0}$
is the reference Ozmidov length defined by (2.4). The convective Reynolds number is defined as
![]() $Re_{\ast }\equiv z_{enc}w_{\ast }/\unicode[STIX]{x1D708}$
, where
$Re_{\ast }\equiv z_{enc}w_{\ast }/\unicode[STIX]{x1D708}$
, where
![]() $w_{\ast }$
is the convective velocity scale defined by (2.13). The turbulent Reynolds number is defined as
$w_{\ast }$
is the convective velocity scale defined by (2.13). The turbulent Reynolds number is defined as
![]() $Re_{t}\equiv e^{2}/\unicode[STIX]{x1D700}\unicode[STIX]{x1D708}$
, where
$Re_{t}\equiv e^{2}/\unicode[STIX]{x1D700}\unicode[STIX]{x1D708}$
, where
![]() $e$
is the TKE and
$e$
is the TKE and
![]() $\unicode[STIX]{x1D700}$
its viscous dissipation rate;
$\unicode[STIX]{x1D700}$
its viscous dissipation rate;
![]() $(Re_{t})_{max}$
is the maximum turbulent Reynolds number in the CBL; and
$(Re_{t})_{max}$
is the maximum turbulent Reynolds number in the CBL; and
![]() $(Re_{t})_{z_{i,f}}$
is the turbulent Reynolds number particularized at the height of the minimum buoyancy flux.
$(Re_{t})_{z_{i,f}}$
is the turbulent Reynolds number particularized at the height of the minimum buoyancy flux.
![]() $(Re_{b})_{z_{i,f}}$
is the buoyancy Reynolds number defined by (2.7) particularized at the height of the minimum buoyancy flux;
$(Re_{b})_{z_{i,f}}$
is the buoyancy Reynolds number defined by (2.7) particularized at the height of the minimum buoyancy flux;
![]() $\unicode[STIX]{x1D702}\equiv (\unicode[STIX]{x1D708}^{3}/\unicode[STIX]{x1D700})^{1/4}$
is the Kolmogorov scale;
$\unicode[STIX]{x1D702}\equiv (\unicode[STIX]{x1D708}^{3}/\unicode[STIX]{x1D700})^{1/4}$
is the Kolmogorov scale;
![]() $(\unicode[STIX]{x0394}z_{i})_{c}$
and
$(\unicode[STIX]{x0394}z_{i})_{c}$
and
![]() $(\unicode[STIX]{x0394}z_{i})_{s}$
are defined by (4.9) and (4.10), respectively, and are the convective and shear limits of the entrainment-zone scale, which is defined by (4.6);
$(\unicode[STIX]{x0394}z_{i})_{s}$
are defined by (4.9) and (4.10), respectively, and are the convective and shear limits of the entrainment-zone scale, which is defined by (4.6);
![]() $L_{Ob}$
is the Obukhov length defined by (2.11).
$L_{Ob}$
is the Obukhov length defined by (2.11).
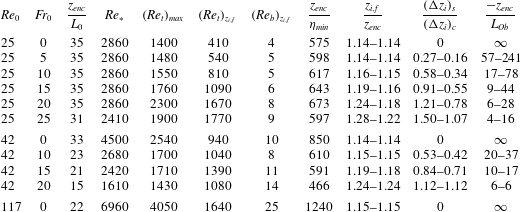
In our simulations, we fix
![]() $Pr=1$
and change the reference Froude number between zero (no wind condition) and 25 (strong wind condition) in intervals of 5. Table 1 summarizes the configurations studied in this work. We reach
$Pr=1$
and change the reference Froude number between zero (no wind condition) and 25 (strong wind condition) in intervals of 5. Table 1 summarizes the configurations studied in this work. We reach
![]() $z_{enc}/L_{0}\simeq 35$
, covering in this way a large extent of the typical values observed in nature. The stability parameter
$z_{enc}/L_{0}\simeq 35$
, covering in this way a large extent of the typical values observed in nature. The stability parameter
![]() $-z_{enc}/L_{Ob}$
is larger than 4. Hence, we cover the regime of weakly unstable conditions
$-z_{enc}/L_{Ob}$
is larger than 4. Hence, we cover the regime of weakly unstable conditions
![]() $0<-z_{enc}/L_{Ob}\lesssim 15{-}20$
, characterized by horizontal convective rolls aligned with the mean wind direction, as well as the regime of strongly unstable conditions, characterized by polygonal convective cells (LeMone Reference Lemone1973; Moeng & Sullivan Reference Moeng and Sullivan1994; Salesky et al.
Reference Salesky, Chamecki and Bou-Zeid2017). The reference Reynolds number that we achieve in our simulations, however, is much smaller than in the atmosphere. Nonetheless, the entrainment zone is largely occupied with turbulent patches, as shown in figure 2. We use data from simulations with
$0<-z_{enc}/L_{Ob}\lesssim 15{-}20$
, characterized by horizontal convective rolls aligned with the mean wind direction, as well as the regime of strongly unstable conditions, characterized by polygonal convective cells (LeMone Reference Lemone1973; Moeng & Sullivan Reference Moeng and Sullivan1994; Salesky et al.
Reference Salesky, Chamecki and Bou-Zeid2017). The reference Reynolds number that we achieve in our simulations, however, is much smaller than in the atmosphere. Nonetheless, the entrainment zone is largely occupied with turbulent patches, as shown in figure 2. We use data from simulations with
![]() $Re_{0}=25$
,
$Re_{0}=25$
,
![]() $Re_{0}=42$
and
$Re_{0}=42$
and
![]() $Re_{0}=117$
. The main analysis is based on the simulations with
$Re_{0}=117$
. The main analysis is based on the simulations with
![]() $Re_{0}=25$
because these cases reach higher values of state of development
$Re_{0}=25$
because these cases reach higher values of state of development
![]() $z_{enc}/L_{0}$
, and, unless otherwise stated, the figures show data from these simulations. The cases with
$z_{enc}/L_{0}$
, and, unless otherwise stated, the figures show data from these simulations. The cases with
![]() $Re_{0}=42$
are used to study the sensitivity of the results to the Reynolds number; for the shear-free cases, we also compare to case
$Re_{0}=42$
are used to study the sensitivity of the results to the Reynolds number; for the shear-free cases, we also compare to case
![]() $Re_{0}=117$
. Although this range of Reynolds number is small, the observed tendency towards Reynolds-number similarity is consistent with that observed in previous work in similar configurations, and supports the use of DNS to study some aspects of the atmospheric boundary layer (Jonker et al.
Reference Jonker, van Reeuwijk, Sullivan and Patton2013; Waggy, Biringen & Sullivan Reference Waggy, Biringen and Sullivan2013; Garcia & Mellado Reference Garcia and Mellado2014; van Heerwaarden & Mellado Reference van Heerwaarden and Mellado2016; Mellado et al.
Reference Mellado, Bretherton, Stevens and Wyant2018).
$Re_{0}=117$
. Although this range of Reynolds number is small, the observed tendency towards Reynolds-number similarity is consistent with that observed in previous work in similar configurations, and supports the use of DNS to study some aspects of the atmospheric boundary layer (Jonker et al.
Reference Jonker, van Reeuwijk, Sullivan and Patton2013; Waggy, Biringen & Sullivan Reference Waggy, Biringen and Sullivan2013; Garcia & Mellado Reference Garcia and Mellado2014; van Heerwaarden & Mellado Reference van Heerwaarden and Mellado2016; Mellado et al.
Reference Mellado, Bretherton, Stevens and Wyant2018).

Figure 2. Horizontal cross-section of the standardized natural logarithm of the viscous dissipation rate
![]() $\unicode[STIX]{x1D716}\equiv \unicode[STIX]{x1D708}(\unicode[STIX]{x2202}_{i}u_{j}^{\prime }+\unicode[STIX]{x2202}_{j}u_{i}^{\prime })\unicode[STIX]{x2202}_{j}u_{i}^{\prime }$
at the height of the minimum buoyancy flux from case
$\unicode[STIX]{x1D716}\equiv \unicode[STIX]{x1D708}(\unicode[STIX]{x2202}_{i}u_{j}^{\prime }+\unicode[STIX]{x2202}_{j}u_{i}^{\prime })\unicode[STIX]{x2202}_{j}u_{i}^{\prime }$
at the height of the minimum buoyancy flux from case
![]() $Fr_{0}=20$
and
$Fr_{0}=20$
and
![]() $Re_{0}=42$
of table 1 at
$Re_{0}=42$
of table 1 at
![]() $z_{enc}/L_{0}\simeq 15$
. Primes indicate turbulent-fluctuation fields.
$z_{enc}/L_{0}\simeq 15$
. Primes indicate turbulent-fluctuation fields.
The domain size is
![]() $215L_{0}\times 215L_{0}\times 130L_{0}$
in all cases, and stopping the simulation at
$215L_{0}\times 215L_{0}\times 130L_{0}$
in all cases, and stopping the simulation at
![]() $z_{enc}/L_{0}\simeq 35$
implies that the boundary layer occupies approximately
$z_{enc}/L_{0}\simeq 35$
implies that the boundary layer occupies approximately
![]() $30\,\%$
of the computational domain. Preliminary studies have shown that this ratio between the CBL depth and the depth of the computational domain is small enough for results to be independent of the depth of the computational domain. The aspect ratio of the horizontal domain size and the CBL depth varies between
$30\,\%$
of the computational domain. Preliminary studies have shown that this ratio between the CBL depth and the depth of the computational domain is small enough for results to be independent of the depth of the computational domain. The aspect ratio of the horizontal domain size and the CBL depth varies between
![]() $12:1$
at the beginning of the quasi-steady regime to around
$12:1$
at the beginning of the quasi-steady regime to around
![]() $5:1$
at the final time considered in the analysis. The thickness
$5:1$
at the final time considered in the analysis. The thickness
![]() $\unicode[STIX]{x1D6FF}_{0}$
used in the initial conditions (2.2) and (2.3) is
$\unicode[STIX]{x1D6FF}_{0}$
used in the initial conditions (2.2) and (2.3) is
![]() $\unicode[STIX]{x1D6FF}_{0}\simeq 0.2L_{0}$
, small compared to
$\unicode[STIX]{x1D6FF}_{0}\simeq 0.2L_{0}$
, small compared to
![]() $z_{enc}\simeq 10L_{0}$
, which is when the quasi-steady regime in shear-free CBLs starts. Preliminary studies considering additional perturbations in the velocity field over a similarly thin region have shown that results are independent of the details of the initial conditions.
$z_{enc}\simeq 10L_{0}$
, which is when the quasi-steady regime in shear-free CBLs starts. Preliminary studies considering additional perturbations in the velocity field over a similarly thin region have shown that results are independent of the details of the initial conditions.
Table 2. Grid resolution. Here
![]() $\unicode[STIX]{x1D6E5}_{x}$
,
$\unicode[STIX]{x1D6E5}_{x}$
,
![]() $\unicode[STIX]{x1D6E5}_{y}$
and
$\unicode[STIX]{x1D6E5}_{y}$
and
![]() $\unicode[STIX]{x1D6E5}_{z}$
are the grid spacings in the streamwise, spanwise and vertical directions, respectively. The maximum value of
$\unicode[STIX]{x1D6E5}_{z}$
are the grid spacings in the streamwise, spanwise and vertical directions, respectively. The maximum value of
![]() $\unicode[STIX]{x1D6E5}_{z}/\unicode[STIX]{x1D702}$
occurs at the final time of the simulations, while the maximum values of
$\unicode[STIX]{x1D6E5}_{z}/\unicode[STIX]{x1D702}$
occurs at the final time of the simulations, while the maximum values of
![]() $\unicode[STIX]{x1D6E5}_{x}^{+}$
,
$\unicode[STIX]{x1D6E5}_{x}^{+}$
,
![]() $\unicode[STIX]{x1D6E5}_{y}^{+}$
and
$\unicode[STIX]{x1D6E5}_{y}^{+}$
and
![]() $\unicode[STIX]{x1D6E5}_{z}^{+}$
take place at the very beginning of the simulations, when the friction velocity is large. The last column shows the variation between
$\unicode[STIX]{x1D6E5}_{z}^{+}$
take place at the very beginning of the simulations, when the friction velocity is large. The last column shows the variation between
![]() $z_{enc}/L_{0}=15$
and the final time of the simulations.
$z_{enc}/L_{0}=15$
and the final time of the simulations.
Apart from the case
![]() $Fr_{0}=20$
, the grid spacings are uniform and isotropic in all of the computational domain except near the surface and in the free atmosphere above the turbulent boundary layer (see table 2). As we move towards the surface, the vertical grid spacing is smoothly refined according to a hyperbolic tangent profile to provide the required higher resolution near the surface. The ratio between the vertical grid spacing in the bulk of the CBL and near the surface is 2.5, which is roughly the ratio between the Kolmogorov length scale in the bulk of the turbulent layer and near the surface in convection-dominated flows (Shishkina et al.
Reference Shishkina, Stevens, Grossmann and Lohse2010; Mellado Reference Mellado2012). The grid stretching associated with this refinement concentrates between
$Fr_{0}=20$
, the grid spacings are uniform and isotropic in all of the computational domain except near the surface and in the free atmosphere above the turbulent boundary layer (see table 2). As we move towards the surface, the vertical grid spacing is smoothly refined according to a hyperbolic tangent profile to provide the required higher resolution near the surface. The ratio between the vertical grid spacing in the bulk of the CBL and near the surface is 2.5, which is roughly the ratio between the Kolmogorov length scale in the bulk of the turbulent layer and near the surface in convection-dominated flows (Shishkina et al.
Reference Shishkina, Stevens, Grossmann and Lohse2010; Mellado Reference Mellado2012). The grid stretching associated with this refinement concentrates between
![]() $z=3L_{0}$
and
$z=3L_{0}$
and
![]() $z=15L_{0}$
and the stretching factor is less than 1.5 %, which has been shown to be small enough to maintain the high accuracy of the compact schemes used in this work (Mellado & Ansorge Reference Mellado and Ansorge2012). As we move upwards outside of the turbulent boundary layer and into the non-turbulent free atmosphere, the vertical grid spacing is smoothly coarsened according to a second hyperbolic tangent profile. The aim is to extend the vertical size of the computational domain and reduce the effect of the spurious reflection of gravity waves at the top of the computational domain without an excessive penalty in the required number of grid points. This coarsening starts beyond
$z=15L_{0}$
and the stretching factor is less than 1.5 %, which has been shown to be small enough to maintain the high accuracy of the compact schemes used in this work (Mellado & Ansorge Reference Mellado and Ansorge2012). As we move upwards outside of the turbulent boundary layer and into the non-turbulent free atmosphere, the vertical grid spacing is smoothly coarsened according to a second hyperbolic tangent profile. The aim is to extend the vertical size of the computational domain and reduce the effect of the spurious reflection of gravity waves at the top of the computational domain without an excessive penalty in the required number of grid points. This coarsening starts beyond
![]() $z=55L_{0}$
, which is well above the turbulent boundary layer, and the corresponding stretching factor is less than 3.5 %. We used preliminary studies to ascertain that the results were insensitive to the details of the grid.
$z=55L_{0}$
, which is well above the turbulent boundary layer, and the corresponding stretching factor is less than 3.5 %. We used preliminary studies to ascertain that the results were insensitive to the details of the grid.
The grid spacings are chosen according to the well-established resolution requirements for shear-driven flows (Flores, Jiménez & Del Álamo Reference Flores, Jiménez and Del Álamo2007; Spalart, Coleman & Johnstone Reference Spalart, Coleman and Johnstone2008; Bernardini, Pirozzoli & Orlandi Reference Bernardini, Pirozzoli and Orlandi2014) and convection-driven flows (Shishkina et al.
Reference Shishkina, Stevens, Grossmann and Lohse2010; Mellado Reference Mellado2012; Waggy et al.
Reference Waggy, Biringen and Sullivan2013). The vertical grid spacing,
![]() $\unicode[STIX]{x1D6E5}_{z}$
, always satisfies the relation
$\unicode[STIX]{x1D6E5}_{z}$
, always satisfies the relation
![]() $\unicode[STIX]{x1D6E5}_{z}/\unicode[STIX]{x1D702}\lesssim 1.5$
(cf. table 2), where
$\unicode[STIX]{x1D6E5}_{z}/\unicode[STIX]{x1D702}\lesssim 1.5$
(cf. table 2), where
![]() $\unicode[STIX]{x1D702}\equiv (\unicode[STIX]{x1D708}^{3}/\unicode[STIX]{x1D700})^{1/4}$
is the Kolmogorov scale. This ratio is sufficient for the statistical properties of interest to depend less than
$\unicode[STIX]{x1D702}\equiv (\unicode[STIX]{x1D708}^{3}/\unicode[STIX]{x1D700})^{1/4}$
is the Kolmogorov scale. This ratio is sufficient for the statistical properties of interest to depend less than
![]() $5\,\%$
on the grid spacing, which is comparable to or less than the statistical convergence of the properties considered in the present work (Mellado Reference Mellado2012; Garcia & Mellado Reference Garcia and Mellado2014). We also keep
$5\,\%$
on the grid spacing, which is comparable to or less than the statistical convergence of the properties considered in the present work (Mellado Reference Mellado2012; Garcia & Mellado Reference Garcia and Mellado2014). We also keep
![]() $\unicode[STIX]{x1D6E5}_{x}^{+}=\unicode[STIX]{x1D6E5}_{y}^{+}\lesssim 4.5$
, where superscript
$\unicode[STIX]{x1D6E5}_{x}^{+}=\unicode[STIX]{x1D6E5}_{y}^{+}\lesssim 4.5$
, where superscript
![]() $+$
denotes quantities normalized with the wall unit
$+$
denotes quantities normalized with the wall unit
![]() $\unicode[STIX]{x1D708}/u_{\ast }$
(Ansorge & Mellado Reference Ansorge and Mellado2014; Gohari & Sarkar Reference Gohari and Sarkar2017; Pirozzoli et al.
Reference Pirozzoli, Bernardini, Verzicco and Orlandi2017). Moreover, the viscous sublayer is resolved by
$\unicode[STIX]{x1D708}/u_{\ast }$
(Ansorge & Mellado Reference Ansorge and Mellado2014; Gohari & Sarkar Reference Gohari and Sarkar2017; Pirozzoli et al.
Reference Pirozzoli, Bernardini, Verzicco and Orlandi2017). Moreover, the viscous sublayer is resolved by
![]() $\simeq 10$
grid points in all simulations (Spalart et al.
Reference Spalart, Coleman and Johnstone2008; Gohari & Sarkar Reference Gohari and Sarkar2017). The reason for the anisotropic grid in the horizontal directions in the cases with
$\simeq 10$
grid points in all simulations (Spalart et al.
Reference Spalart, Coleman and Johnstone2008; Gohari & Sarkar Reference Gohari and Sarkar2017). The reason for the anisotropic grid in the horizontal directions in the cases with
![]() $Fr_{0}=20$
is that we could satisfy the aforementioned resolution constraints without the need to reduce the grid spacing in the streamwise direction with respect to the corresponding cases with
$Fr_{0}=20$
is that we could satisfy the aforementioned resolution constraints without the need to reduce the grid spacing in the streamwise direction with respect to the corresponding cases with
![]() $Fr_{0}=15$
, which allowed us to save computational time.
$Fr_{0}=15$
, which allowed us to save computational time.
To improve statistical convergence and thus the clarity of the results discussed below, horizontal averages are additionally averaged in time over an interval
![]() $\unicode[STIX]{x0394}z_{enc}/L_{0}=2$
, which means
$\unicode[STIX]{x0394}z_{enc}/L_{0}=2$
, which means
![]() $\simeq 6$
large-eddy turnover times at
$\simeq 6$
large-eddy turnover times at
![]() $z_{enc}/L_{0}=30$
. This time interval is small compared to the time required for the mean properties to change significantly. When plotting the data, lines indicate this running average within an interval
$z_{enc}/L_{0}=30$
. This time interval is small compared to the time required for the mean properties to change significantly. When plotting the data, lines indicate this running average within an interval
![]() $\unicode[STIX]{x0394}z_{enc}/L_{0}=2$
, and shadow regions indicate the interval of two standard deviations around that average.
$\unicode[STIX]{x0394}z_{enc}/L_{0}=2$
, and shadow regions indicate the interval of two standard deviations around that average.
2.4 Equilibrium (quasi-steady) entrainment regime
Garcia & Mellado (Reference Garcia and Mellado2014) have shown that the equilibrium (quasi-steady) entrainment regime is reached beyond
![]() $z_{enc}/L_{0}\simeq 10$
in shear-free CBLs growing into linearly stratified atmospheres. In order to evaluate if the wind shear changes this critical value, following Fedorovich et al. (Reference Fedorovich, Conzemius and Mironov2004b
), we perform an integral analysis of the TKE evolution equation
$z_{enc}/L_{0}\simeq 10$
in shear-free CBLs growing into linearly stratified atmospheres. In order to evaluate if the wind shear changes this critical value, following Fedorovich et al. (Reference Fedorovich, Conzemius and Mironov2004b
), we perform an integral analysis of the TKE evolution equation
where
![]() $\unicode[STIX]{x2202}_{t}e$
is the accumulation term,
$\unicode[STIX]{x2202}_{t}e$
is the accumulation term,
![]() $P\equiv -\langle u^{\prime }w^{\prime }\rangle \unicode[STIX]{x2202}_{z}\langle u\rangle$
is the shear-production rate,
$P\equiv -\langle u^{\prime }w^{\prime }\rangle \unicode[STIX]{x2202}_{z}\langle u\rangle$
is the shear-production rate,
![]() $\langle b^{\prime }w^{\prime }\rangle$
is the buoyancy production or destruction rate,
$\langle b^{\prime }w^{\prime }\rangle$
is the buoyancy production or destruction rate,
![]() $-\unicode[STIX]{x2202}_{z}T$
is the turbulent transport, where
$-\unicode[STIX]{x2202}_{z}T$
is the turbulent transport, where
![]() $T\equiv \langle u_{i}^{\prime }u_{i}^{\prime }w^{\prime }/2+p^{\prime }w^{\prime }-u_{i}^{\prime }\unicode[STIX]{x1D70F}_{i3}^{\prime }\rangle$
, and
$T\equiv \langle u_{i}^{\prime }u_{i}^{\prime }w^{\prime }/2+p^{\prime }w^{\prime }-u_{i}^{\prime }\unicode[STIX]{x1D70F}_{i3}^{\prime }\rangle$
, and
![]() $\unicode[STIX]{x1D700}\equiv \langle \unicode[STIX]{x1D70F}_{ij}^{\prime }\unicode[STIX]{x2202}_{j}u_{i}^{\prime }\rangle$
is the viscous dissipation rate,
$\unicode[STIX]{x1D700}\equiv \langle \unicode[STIX]{x1D70F}_{ij}^{\prime }\unicode[STIX]{x2202}_{j}u_{i}^{\prime }\rangle$
is the viscous dissipation rate,
![]() $\unicode[STIX]{x1D70F}_{ij}\equiv \unicode[STIX]{x1D708}(\unicode[STIX]{x2202}_{i}u_{j}+\unicode[STIX]{x2202}_{j}u_{i})$
being the kinematic components of the viscous stress tensor. Primes indicate turbulent-fluctuation fields, e.g.
$\unicode[STIX]{x1D70F}_{ij}\equiv \unicode[STIX]{x1D708}(\unicode[STIX]{x2202}_{i}u_{j}+\unicode[STIX]{x2202}_{j}u_{i})$
being the kinematic components of the viscous stress tensor. Primes indicate turbulent-fluctuation fields, e.g.
![]() $b^{\prime }\equiv b-\langle b\rangle$
. Integrating (2.14) from the surface to a height
$b^{\prime }\equiv b-\langle b\rangle$
. Integrating (2.14) from the surface to a height
![]() $z_{\infty }$
far into the non-turbulent free atmosphere yields
$z_{\infty }$
far into the non-turbulent free atmosphere yields
which for simplicity we write as
The temporal evolution of each term normalized by
![]() $w_{\ast }^{3}$
is shown in figure 3. (Curves in this figure correspond to the upper limit of integration
$w_{\ast }^{3}$
is shown in figure 3. (Curves in this figure correspond to the upper limit of integration
![]() $z_{\infty }=2.5z_{enc}$
, but results remain similar when varying this limit between
$z_{\infty }=2.5z_{enc}$
, but results remain similar when varying this limit between
![]() $1.5z_{enc}$
and
$1.5z_{enc}$
and
![]() $2.5z_{enc}$
.) Similar to the shear-free case, the normalized integral of the transport term
$2.5z_{enc}$
.) Similar to the shear-free case, the normalized integral of the transport term
![]() $I_{T}$
is small, which implies that the energy drain due to the upward radiation of gravity waves is negligible. Moreover, the normalized integral of the temporal term
$I_{T}$
is small, which implies that the energy drain due to the upward radiation of gravity waves is negligible. Moreover, the normalized integral of the temporal term
![]() $I_{t}$
becomes negligible beyond
$I_{t}$
becomes negligible beyond
![]() $z_{enc}/L_{0}\simeq 10$
–15, implying that there is a balance between shear production, buoyancy production and viscous dissipation, i.e.
$z_{enc}/L_{0}\simeq 10$
–15, implying that there is a balance between shear production, buoyancy production and viscous dissipation, i.e.
![]() $I_{bw}+I_{P}\simeq I_{\unicode[STIX]{x1D700}}$
. This balance corresponds to the equilibrium (quasi-steady) entrainment regime. In this work, we focus on this regime and study wind-shear effects beyond
$I_{bw}+I_{P}\simeq I_{\unicode[STIX]{x1D700}}$
. This balance corresponds to the equilibrium (quasi-steady) entrainment regime. In this work, we focus on this regime and study wind-shear effects beyond
![]() $z_{enc}/L_{0}\simeq 15$
, and we will only consider the data in the quasi-steady regime to derive scaling laws. However, we will plot the data starting at
$z_{enc}/L_{0}\simeq 15$
, and we will only consider the data in the quasi-steady regime to derive scaling laws. However, we will plot the data starting at
![]() $z_{enc}/L_{0}=5$
to indicate how the statistics approach the quasi-steady regime.
$z_{enc}/L_{0}=5$
to indicate how the statistics approach the quasi-steady regime.
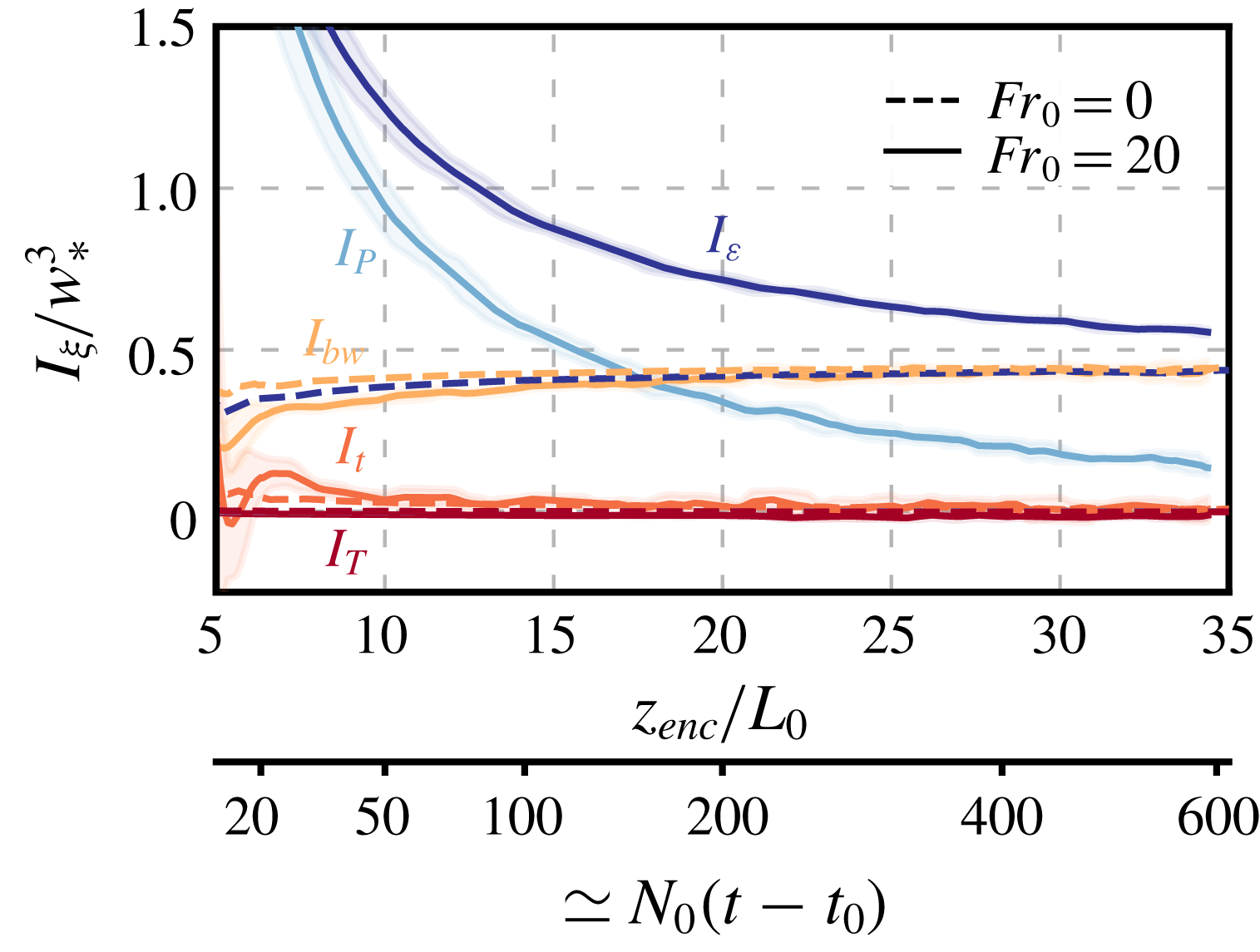
Figure 3. Temporal evolution of the terms of the integral TKE budget equation (2.16) normalized with the convective velocity scale, defined in (2.13). Lines indicate the average within an interval
![]() $\unicode[STIX]{x0394}z_{enc}/L_{0}=2$
, and shadow regions indicate the interval of two standard deviations around that average.
$\unicode[STIX]{x0394}z_{enc}/L_{0}=2$
, and shadow regions indicate the interval of two standard deviations around that average.
3 Wind-shear effects on buoyancy and velocity
In this section, we discuss the dependence of buoyancy and velocity properties on
![]() $Fr_{0}$
and
$Fr_{0}$
and
![]() $z_{enc}/L_{0}$
, obtaining the values of these quantities for which wind-shear effects become significant. Consistently with previous studies, some properties, like horizontal-velocity statistics, vary monotonically with the Froude number, some properties, like the buoyancy flux in the entrainment zone, change significantly only when
$z_{enc}/L_{0}$
, obtaining the values of these quantities for which wind-shear effects become significant. Consistently with previous studies, some properties, like horizontal-velocity statistics, vary monotonically with the Froude number, some properties, like the buoyancy flux in the entrainment zone, change significantly only when
![]() $Fr_{0}\gtrsim 10$
, and some properties, like the buoyancy and vertical-velocity statistics in the mixed layer, remain approximately unchanged and follow shear-free scaling laws for all conditions considered in this study. In the following sections, we will rationalize this behaviour.
$Fr_{0}\gtrsim 10$
, and some properties, like the buoyancy and vertical-velocity statistics in the mixed layer, remain approximately unchanged and follow shear-free scaling laws for all conditions considered in this study. In the following sections, we will rationalize this behaviour.
3.1 Effects on the buoyancy
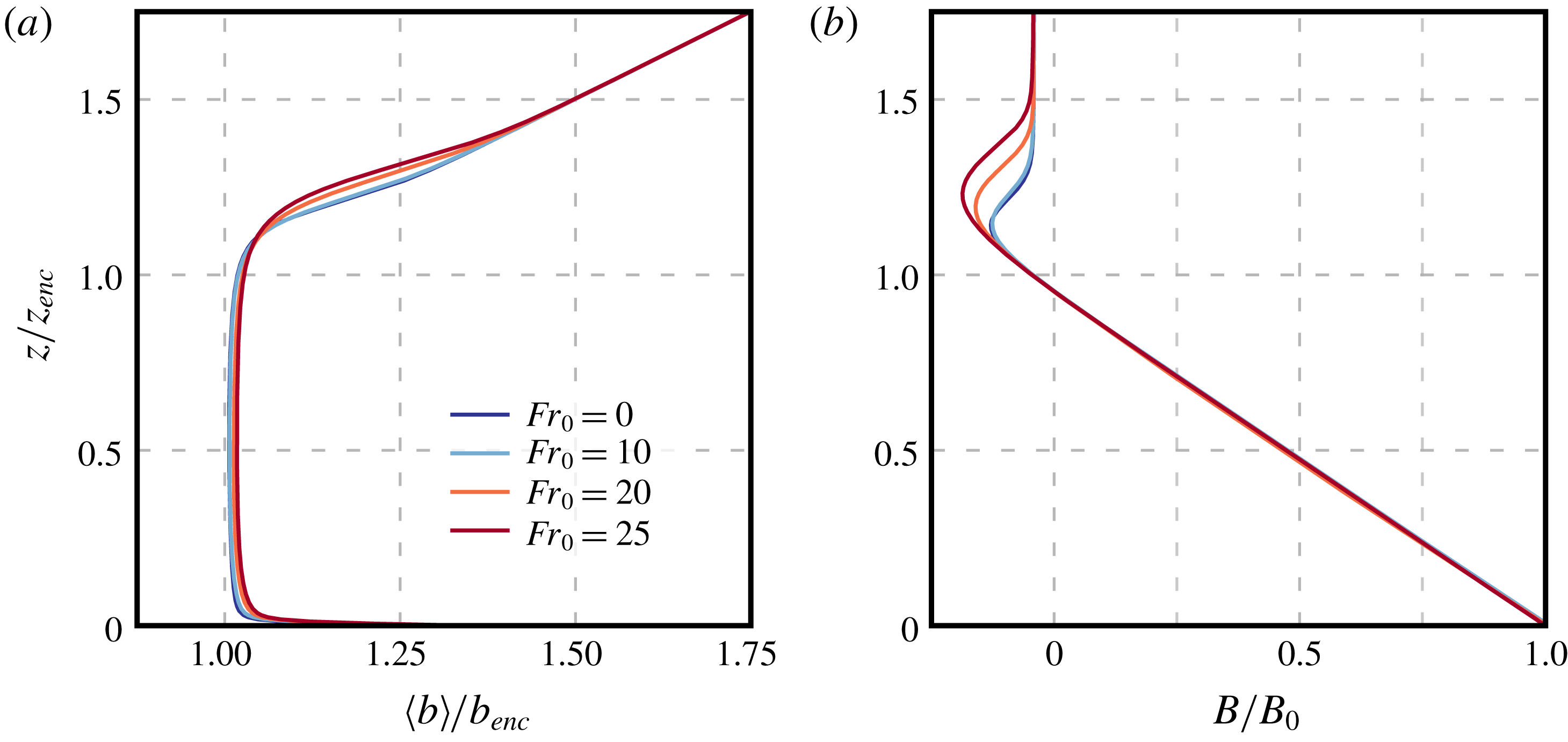
Figure 4. Vertical profiles of (a) the mean buoyancy normalized by the encroachment buoyancy, defined by (3.1), and (b) the buoyancy flux, defined by (3.2), normalized by the surface buoyancy flux, for different Froude numbers at
![]() $z_{enc}/L_{0}\simeq 30$
. Data have been averaged within an interval
$z_{enc}/L_{0}\simeq 30$
. Data have been averaged within an interval
![]() $\unicode[STIX]{x0394}z_{enc}/L_{0}=2$
.
$\unicode[STIX]{x0394}z_{enc}/L_{0}=2$
.
In the mixed layer, i.e. the well-mixed region between
![]() $z\simeq 0.1z_{enc}$
and
$z\simeq 0.1z_{enc}$
and
![]() $z\simeq z_{enc}$
, the mean buoyancy increases in time due to the surface buoyancy flux and the entrainment flux. In our study, the surface flux is constant and independent of the wind velocity, but the entrainment flux increases with the wind velocity, and therefore the mean buoyancy in the mixed layer is expected to increase with
$z\simeq z_{enc}$
, the mean buoyancy increases in time due to the surface buoyancy flux and the entrainment flux. In our study, the surface flux is constant and independent of the wind velocity, but the entrainment flux increases with the wind velocity, and therefore the mean buoyancy in the mixed layer is expected to increase with
![]() $Fr_{0}$
. Previous studies have shown, however, that this increase is weak (e.g. Kim et al.
Reference Kim, Park and Moeng2003; Pino, Vilà-Guerau De Arellano & Duynkerke Reference Pino, Vilà-Guerau De Arellano and Duynkerke2003; Pino & Vilà-Guerau De Arellano Reference Pino and Vilà-Guerau De Arellano2008), so that the encroachment buoyancy (Carson & Smith Reference Carson and Smith1975)
$Fr_{0}$
. Previous studies have shown, however, that this increase is weak (e.g. Kim et al.
Reference Kim, Park and Moeng2003; Pino, Vilà-Guerau De Arellano & Duynkerke Reference Pino, Vilà-Guerau De Arellano and Duynkerke2003; Pino & Vilà-Guerau De Arellano Reference Pino and Vilà-Guerau De Arellano2008), so that the encroachment buoyancy (Carson & Smith Reference Carson and Smith1975)
characterizes the mean buoyancy in the mixed layer not only in shear-free conditions but also in sheared CBLs under weakly to strongly unstable conditions. Figure 4(a) confirms this result up to wind velocities corresponding to
![]() $Fr_{0}=25$
, for which the mean buoyancy is only
$Fr_{0}=25$
, for which the mean buoyancy is only
![]() $\simeq 2$
% higher than in shear-free conditions. Wind-shear effects on the buoyancy flux
$\simeq 2$
% higher than in shear-free conditions. Wind-shear effects on the buoyancy flux
are also negligible in the mixed layer for all Froude numbers considered in this study (figure 4 b). In contrast, in the entrainment zone, the region of negative buoyancy flux above the mixed layer, wind-shear effects become significant for Froude numbers larger than 10. Hence, in agreement with the aforementioned previous studies where Coriolis effects are retained, wind-shear effects on buoyancy properties remain localized inside the entrainment zone for the idealized CBLs considered in this study.
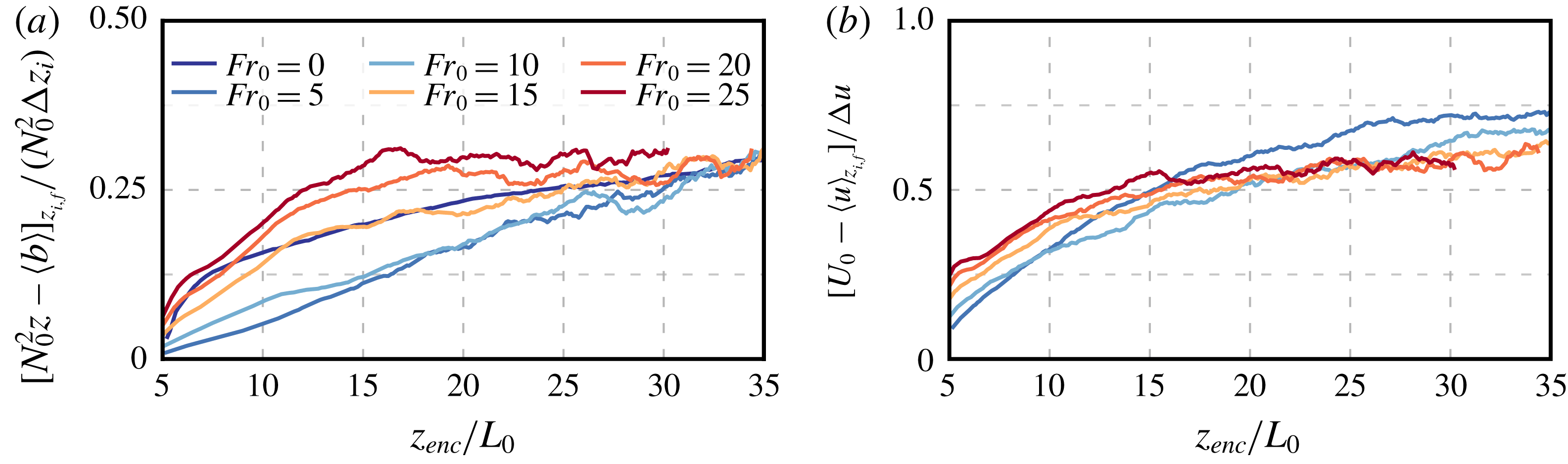
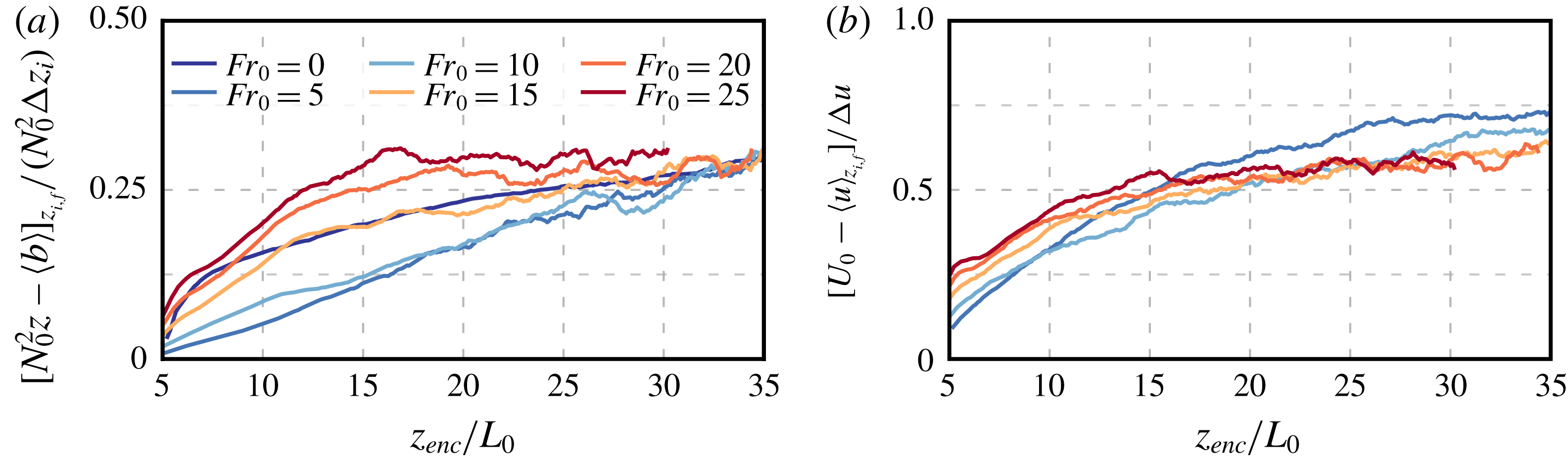
To better quantify the effect of the wind shear on entrainment-zone properties, we plot the temporal evolution of the minimum buoyancy flux normalized by the surface buoyancy flux,
![]() $-B_{z_{i,f}}/B_{0}$
, in figure 5(a). (Henceforth, the subscript
$-B_{z_{i,f}}/B_{0}$
, in figure 5(a). (Henceforth, the subscript
![]() $z_{i,\unicode[STIX]{x1D709}}$
indicates that the corresponding quantity is evaluated at
$z_{i,\unicode[STIX]{x1D709}}$
indicates that the corresponding quantity is evaluated at
![]() $z_{i,\unicode[STIX]{x1D709}}$
, and
$z_{i,\unicode[STIX]{x1D709}}$
, and
![]() $z_{i,f}$
is the height of the minimum buoyancy flux.) For
$z_{i,f}$
is the height of the minimum buoyancy flux.) For
![]() $Fr_{0}\lesssim 10$
, this quantity approximately coincides with that of the shear-free case for
$Fr_{0}\lesssim 10$
, this quantity approximately coincides with that of the shear-free case for
![]() $z_{enc}/L_{0}\gtrsim 10{-}15$
, which indicates a negligible effect of wind shear on the minimum buoyancy flux during the quasi-steady regime. The slight decrease for weak shear conditions
$z_{enc}/L_{0}\gtrsim 10{-}15$
, which indicates a negligible effect of wind shear on the minimum buoyancy flux during the quasi-steady regime. The slight decrease for weak shear conditions
![]() $Fr_{0}=5$
at early states of development
$Fr_{0}=5$
at early states of development
![]() $z_{enc}/L_{0}\lesssim 15$
has also been observed in Pino & Vilà-Guerau De Arellano (Reference Pino and Vilà-Guerau De Arellano2008), and it might be a manifestation of the sheltering effect of shear on the propagation of turbulence near a turbulent/non-turbulent interface (Hunt & Durbin Reference Hunt and Durbin1999; Fedorovich & Thäter Reference Fedorovich and Thäter2001), or of the enhancement of the energy drain from the CBL top by gravity-wave radiation into the free atmosphere (Schröter Reference Schröter2018). However, more analysis would be required to draw a definitive conclusion because the effect of the shear near the surface might still be significant in such a shallow CBL. For Froude numbers larger than 10, the ratio
$z_{enc}/L_{0}\lesssim 15$
has also been observed in Pino & Vilà-Guerau De Arellano (Reference Pino and Vilà-Guerau De Arellano2008), and it might be a manifestation of the sheltering effect of shear on the propagation of turbulence near a turbulent/non-turbulent interface (Hunt & Durbin Reference Hunt and Durbin1999; Fedorovich & Thäter Reference Fedorovich and Thäter2001), or of the enhancement of the energy drain from the CBL top by gravity-wave radiation into the free atmosphere (Schröter Reference Schröter2018). However, more analysis would be required to draw a definitive conclusion because the effect of the shear near the surface might still be significant in such a shallow CBL. For Froude numbers larger than 10, the ratio
![]() $-B_{z_{i,f}}/B_{0}$
increases. Visualizations show that Kelvin–Helmholtz-like instabilities inside the entrainment zone are associated with this increase (cf. figure 1), in agreement with previous observations (Kim et al.
Reference Kim, Park and Moeng2003).
$-B_{z_{i,f}}/B_{0}$
increases. Visualizations show that Kelvin–Helmholtz-like instabilities inside the entrainment zone are associated with this increase (cf. figure 1), in agreement with previous observations (Kim et al.
Reference Kim, Park and Moeng2003).
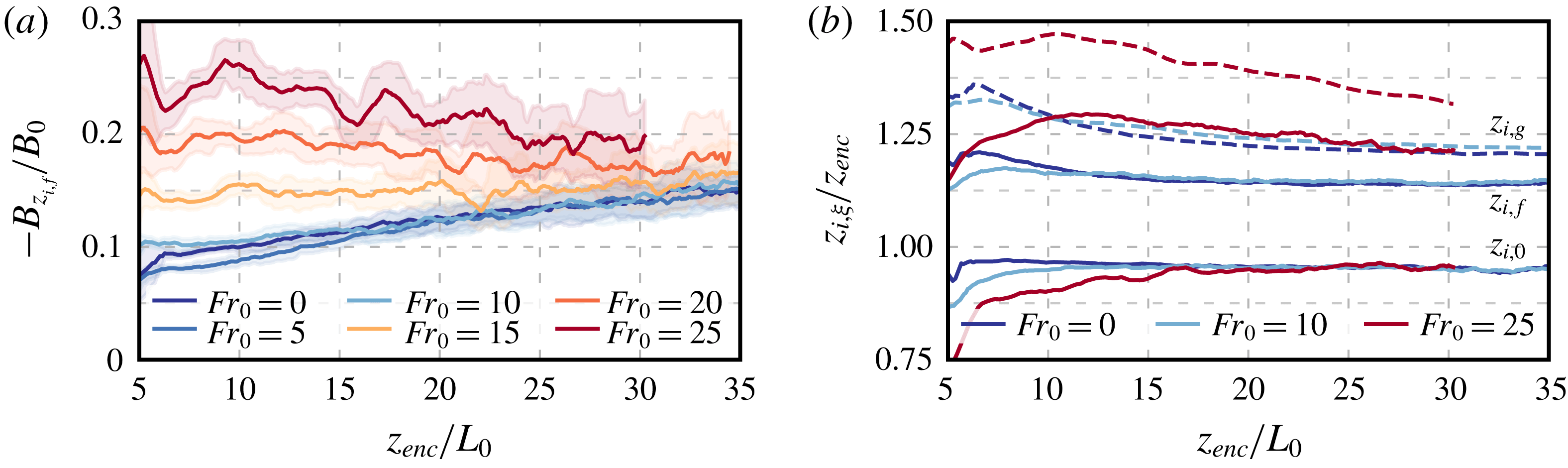
Figure 5. Temporal evolution of (a) the minimum buoyancy flux normalized by the surface buoyancy flux, and (b) different definitions of the CBL depth normalized by the encroachment length scale. For clarity, in panel (b), the height of the maximum buoyancy gradient,
![]() $z_{i,g}$
, is indicated by dashed lines.
$z_{i,g}$
, is indicated by dashed lines.
Another property that proves useful for the analysis of wind-shear effects on entrainment-zone properties is the CBL depth. We consider the following definitions of the CBL depth (see e.g. Garratt Reference Garratt1992; Sullivan et al.
Reference Sullivan, Moeng, Stevens, Lenschow and Mayor1998): (i) the zero-crossing height,
![]() $z_{i,0}$
, where the buoyancy flux becomes zero; (ii) the flux-based height,
$z_{i,0}$
, where the buoyancy flux becomes zero; (ii) the flux-based height,
![]() $z_{i,f}$
, where the buoyancy flux is minimum; and (iii) the gradient-based height,
$z_{i,f}$
, where the buoyancy flux is minimum; and (iii) the gradient-based height,
![]() $z_{i,g}$
, where the mean buoyancy gradient is maximum. The temporal evolution of these heights, shown in figure 5(b), corroborates the features discussed before. First, the zero-crossing height
$z_{i,g}$
, where the mean buoyancy gradient is maximum. The temporal evolution of these heights, shown in figure 5(b), corroborates the features discussed before. First, the zero-crossing height
![]() $z_{i,0}$
, which marks the bottom of the entrainment zone, is independent of the wind strength and it is well approximated by the encroachment length scale,
$z_{i,0}$
, which marks the bottom of the entrainment zone, is independent of the wind strength and it is well approximated by the encroachment length scale,
![]() $z_{enc}$
. This result further indicates that wind-shear effects above the surface layer on the mean buoyancy concentrate in the entrainment zone (Fedorovich & Conzemius Reference Fedorovich and Conzemius2008; Pino & Vilà-Guerau De Arellano Reference Pino and Vilà-Guerau De Arellano2008). Second, the difference in
$z_{enc}$
. This result further indicates that wind-shear effects above the surface layer on the mean buoyancy concentrate in the entrainment zone (Fedorovich & Conzemius Reference Fedorovich and Conzemius2008; Pino & Vilà-Guerau De Arellano Reference Pino and Vilà-Guerau De Arellano2008). Second, the difference in
![]() $z_{i,f}$
and
$z_{i,f}$
and
![]() $z_{i,g}$
between cases
$z_{i,g}$
between cases
![]() $Fr_{0}=0$
and
$Fr_{0}=0$
and
![]() $Fr_{0}=10$
is small, which further indicates that entrainment-zone properties remain unchanged for such a weak wind condition. Third, for stronger wind conditions, wind-shear effects in the entrainment zone become considerable, and both
$Fr_{0}=10$
is small, which further indicates that entrainment-zone properties remain unchanged for such a weak wind condition. Third, for stronger wind conditions, wind-shear effects in the entrainment zone become considerable, and both
![]() $z_{i,f}$
and
$z_{i,f}$
and
![]() $z_{i,g}$
increase. We note that, although the change of these heights is small relative to the CBL depth, those changes are approximately 100 % of the entrainment-zone thickness, and are relevant for the local analysis of the entrainment zone in § 4.
$z_{i,g}$
increase. We note that, although the change of these heights is small relative to the CBL depth, those changes are approximately 100 % of the entrainment-zone thickness, and are relevant for the local analysis of the entrainment zone in § 4.
Figure 5(a,b) also shows that wind-shear effects diminish and eventually vanish as the CBL grows and thermals ascending from the mixed layer become more vigorous and dominate mixing in the entrainment zone (Mahrt & Lenschow Reference Mahrt and Lenschow1976; Pino & Vilà-Guerau De Arellano Reference Pino and Vilà-Guerau De Arellano2008; Liu, Sun & Shen Reference Liu, Sun and Shen2016). Hence, shear effects depend not only on the Froude number
![]() $Fr_{0}$
, or, equivalently, the wind velocity in the free atmosphere, but also on the normalized CBL depth
$Fr_{0}$
, or, equivalently, the wind velocity in the free atmosphere, but also on the normalized CBL depth
![]() $z_{enc}/L_{0}$
. In § 5, we find a non-dimensional variable that embeds the dependence on both
$z_{enc}/L_{0}$
. In § 5, we find a non-dimensional variable that embeds the dependence on both
![]() $Fr_{0}$
and
$Fr_{0}$
and
![]() $z_{enc}/L_{0}$
, which facilitates the characterization of wind-shear effects.
$z_{enc}/L_{0}$
, which facilitates the characterization of wind-shear effects.
3.2 Effects on the velocity
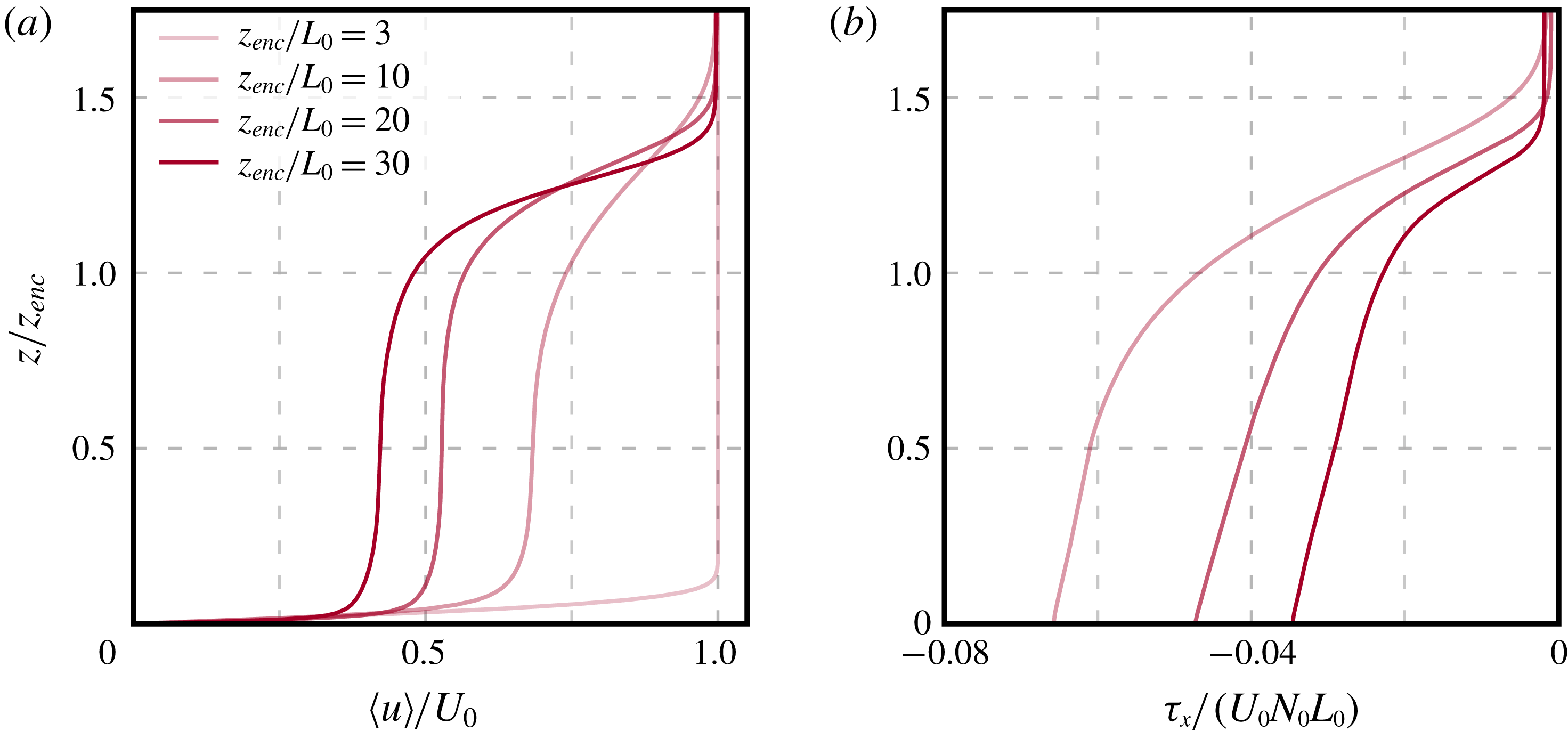
Figure 6. Vertical profiles of (a) the mean streamwise velocity normalized by the wind velocity in the free atmosphere,
![]() $U_{0}$
, and (b) the momentum flux normalized with
$U_{0}$
, and (b) the momentum flux normalized with
![]() $U_{0}$
and the reference convection velocity
$U_{0}$
and the reference convection velocity
![]() $N_{0}L_{0}$
. Data correspond to case
$N_{0}L_{0}$
. Data correspond to case
![]() $Fr_{0}=25$
at different
$Fr_{0}=25$
at different
![]() $z_{enc}/L_{0}$
.
$z_{enc}/L_{0}$
.
As seen in figure 6(a), when the CBL depth becomes an order of magnitude larger than
![]() $L_{0}$
, the velocity profile varies rapidly across the CBL top, and becomes almost flat within the mixed layer. Because of this flat shape, the vertically averaged mean velocity
$L_{0}$
, the velocity profile varies rapidly across the CBL top, and becomes almost flat within the mixed layer. Because of this flat shape, the vertically averaged mean velocity
provides an appropriate characteristic scale, and velocity profiles normalized by
![]() $u_{ml}$
collapse on top of each other and exhibit self-similarity within the mixed layer. This vertical structure consisting of a well-mixed velocity profile in the mixed layer and an elevated wind shear in the entrainment zone is characteristic of the weakly to strongly unstable conditions
$u_{ml}$
collapse on top of each other and exhibit self-similarity within the mixed layer. This vertical structure consisting of a well-mixed velocity profile in the mixed layer and an elevated wind shear in the entrainment zone is characteristic of the weakly to strongly unstable conditions
![]() $-z_{enc}/L_{Ob}\gtrsim 4$
considered in this study (Kim et al.
Reference Kim, Park and Moeng2003; Conzemius & Fedorovich Reference Conzemius and Fedorovich2006a
; Sorbjan Reference Sorbjan2006; Pino & Vilà-Guerau De Arellano Reference Pino and Vilà-Guerau De Arellano2008). Hence, the idealized CBL considered in this study also reproduces this main feature of barotropic CBLs in middle latitudes, despite neglecting Coriolis effects.
$-z_{enc}/L_{Ob}\gtrsim 4$
considered in this study (Kim et al.
Reference Kim, Park and Moeng2003; Conzemius & Fedorovich Reference Conzemius and Fedorovich2006a
; Sorbjan Reference Sorbjan2006; Pino & Vilà-Guerau De Arellano Reference Pino and Vilà-Guerau De Arellano2008). Hence, the idealized CBL considered in this study also reproduces this main feature of barotropic CBLs in middle latitudes, despite neglecting Coriolis effects.
The corresponding profiles of the kinematic momentum flux
are shown in figure 6(b). Horizontal momentum is entrained at the CBL top, transported down across the mixed layer, and finally removed by friction at the surface. The larger magnitude of the momentum flux at the surface compared to the entrainment zone causes the momentum inside the mixed layer to decrease in time (figure 6 a). However, the difference between the momentum flux at the surface and at the CBL top decreases in time, which implies a decrease in the time rate of change of the mean velocity in the mixed layer.
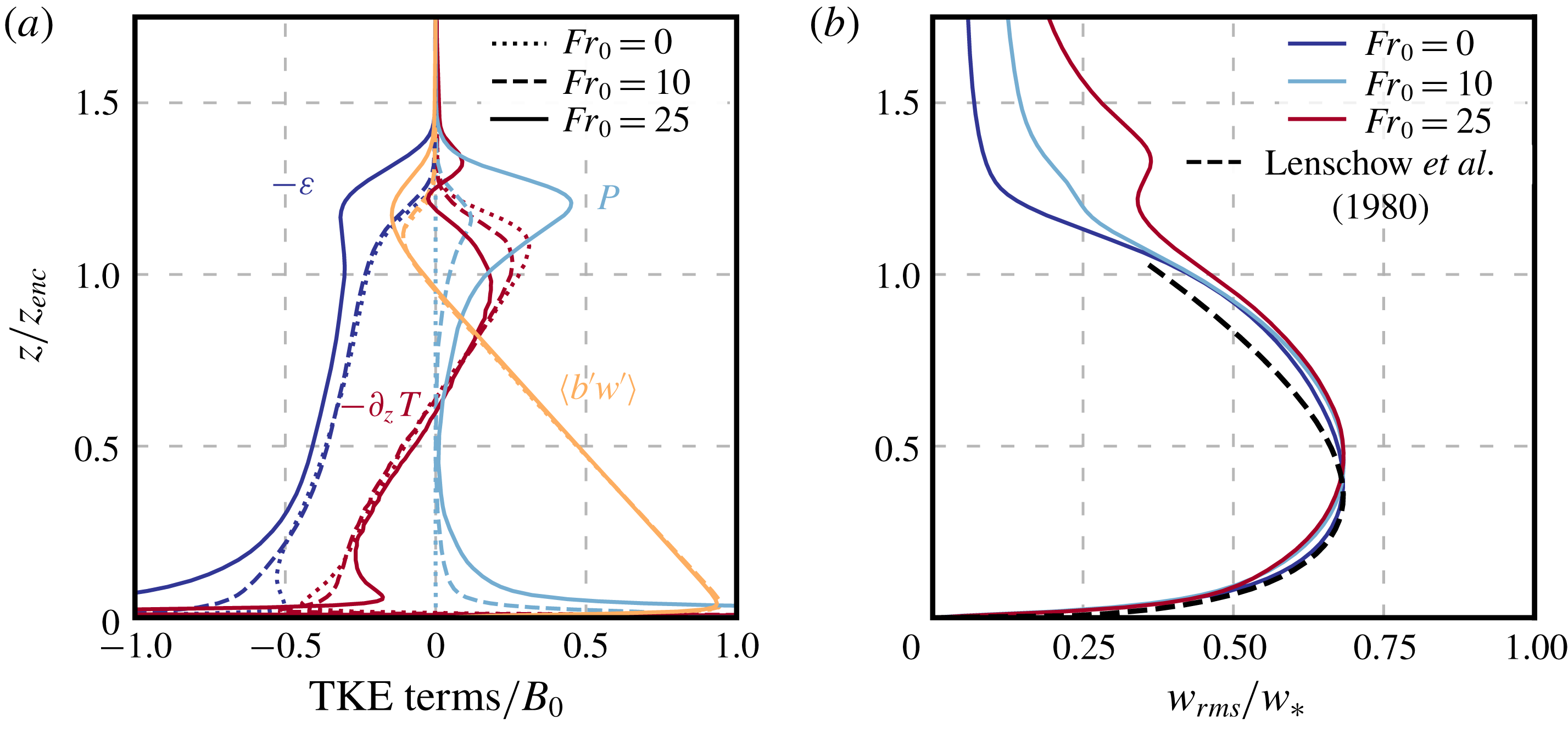
Figure 7. Vertical profiles of (a) the TKE budget and (b) the r.m.s. of the vertical velocity at
![]() $z_{enc}/L_{0}\simeq 30$
. Data from case
$z_{enc}/L_{0}\simeq 30$
. Data from case
![]() $Fr_{0}=10$
correspond to the transition from a convection-dominated regime in the entrainment zone to a shear-dominated regime, and data from case
$Fr_{0}=10$
correspond to the transition from a convection-dominated regime in the entrainment zone to a shear-dominated regime, and data from case
![]() $Fr_{0}=25$
correspond to a shear-dominated regime (
$Fr_{0}=25$
correspond to a shear-dominated regime (
![]() $(\unicode[STIX]{x0394}z_{i})_{s}/(\unicode[STIX]{x0394}z_{i})_{c}\approx 0.43$
and
$(\unicode[STIX]{x0394}z_{i})_{s}/(\unicode[STIX]{x0394}z_{i})_{c}\approx 0.43$
and
![]() $(\unicode[STIX]{x0394}z_{i})_{s}/(\unicode[STIX]{x0394}z_{i})_{c}\approx 1.21$
, respectively; see figure 17 and table 3).
$(\unicode[STIX]{x0394}z_{i})_{s}/(\unicode[STIX]{x0394}z_{i})_{c}\approx 1.21$
, respectively; see figure 17 and table 3).
The TKE budget is shown in figure 7(a). For
![]() $Fr_{0}=10$
, the strong shear production of TKE near the surface changes the transport and dissipation terms, but those changes remain constrained to a depth below
$Fr_{0}=10$
, the strong shear production of TKE near the surface changes the transport and dissipation terms, but those changes remain constrained to a depth below
![]() $\simeq 0.25z_{enc}$
: compared to the shear-free case, the turbulent transport additionally removes energy from very near the surface, below
$\simeq 0.25z_{enc}$
: compared to the shear-free case, the turbulent transport additionally removes energy from very near the surface, below
![]() $\simeq 0.05z_{enc}$
, and deposits it in a thin layer above that region, between
$\simeq 0.05z_{enc}$
, and deposits it in a thin layer above that region, between
![]() $\simeq 0.05z_{enc}$
and
$\simeq 0.05z_{enc}$
and
![]() $\simeq 0.25z_{enc}$
. The turbulent transport remains unchanged in the CBL interior, between
$\simeq 0.25z_{enc}$
. The turbulent transport remains unchanged in the CBL interior, between
![]() $\simeq 0.25z_{enc}$
and
$\simeq 0.25z_{enc}$
and
![]() $\simeq 0.9z_{enc}$
. In the entrainment zone, the reduction of turbulent transport approximately compensates the shear production, while the buoyancy flux and viscous dissipation remain practically the same as in shear-free conditions.
$\simeq 0.9z_{enc}$
. In the entrainment zone, the reduction of turbulent transport approximately compensates the shear production, while the buoyancy flux and viscous dissipation remain practically the same as in shear-free conditions.
For stronger shear conditions, such as for
![]() $Fr_{0}=25$
, the changes near the surface become larger but the turbulent transport still seems to redistribute TKE within a region below
$Fr_{0}=25$
, the changes near the surface become larger but the turbulent transport still seems to redistribute TKE within a region below
![]() $\simeq 0.25z_{enc}$
, which indicates that shear-generated turbulence near the surface is not responsible for the shear enhancement of entrainment (Conzemius & Fedorovich Reference Conzemius and Fedorovich2006a
; Fedorovich & Conzemius Reference Fedorovich and Conzemius2008). In contrast, the changes in the entrainment zone are now more substantial. The turbulent transport develops a local minimum close to zero at the height of maximum shear production, and the magnitudes of the buoyancy flux and dissipation rate increase. We also observe a slight change in the turbulent transport in the CBL interior, a displacement of the curve towards the right. This change indicates that, with respect to the shear-free case, less TKE is being transported from the lower half of the CBL to the upper half, or that shear-generated TKE in the entrainment zone is actually being transported downwards towards the CBL interior. The magnitude of the dissipation rate in the CBL interior increases accordingly.
$\simeq 0.25z_{enc}$
, which indicates that shear-generated turbulence near the surface is not responsible for the shear enhancement of entrainment (Conzemius & Fedorovich Reference Conzemius and Fedorovich2006a
; Fedorovich & Conzemius Reference Fedorovich and Conzemius2008). In contrast, the changes in the entrainment zone are now more substantial. The turbulent transport develops a local minimum close to zero at the height of maximum shear production, and the magnitudes of the buoyancy flux and dissipation rate increase. We also observe a slight change in the turbulent transport in the CBL interior, a displacement of the curve towards the right. This change indicates that, with respect to the shear-free case, less TKE is being transported from the lower half of the CBL to the upper half, or that shear-generated TKE in the entrainment zone is actually being transported downwards towards the CBL interior. The magnitude of the dissipation rate in the CBL interior increases accordingly.
The variance of the vertical velocity, shown in figure 7(b), further stresses the importance of shear across the entrainment zone compared to the shear near the surface, since the curves for different Froude numbers differ for
![]() $z\gtrsim z_{enc}$
but approximately collapse on top of each other for
$z\gtrsim z_{enc}$
but approximately collapse on top of each other for
![]() $z\lesssim z_{enc}$
. In this region, the parametrization for
$z\lesssim z_{enc}$
. In this region, the parametrization for
![]() $w_{rms}$
proposed by Lenschow, Wyngaard & Pennell (Reference Lenschow, Wyngaard and Pennell1980) provides accurate estimates for the weakly to strongly unstable conditions
$w_{rms}$
proposed by Lenschow, Wyngaard & Pennell (Reference Lenschow, Wyngaard and Pennell1980) provides accurate estimates for the weakly to strongly unstable conditions
![]() $-z_{enc}/L_{Ob}\gtrsim 4$
considered here.
$-z_{enc}/L_{Ob}\gtrsim 4$
considered here.
4 Wind-shear effects on the entrainment-zone vertical structure
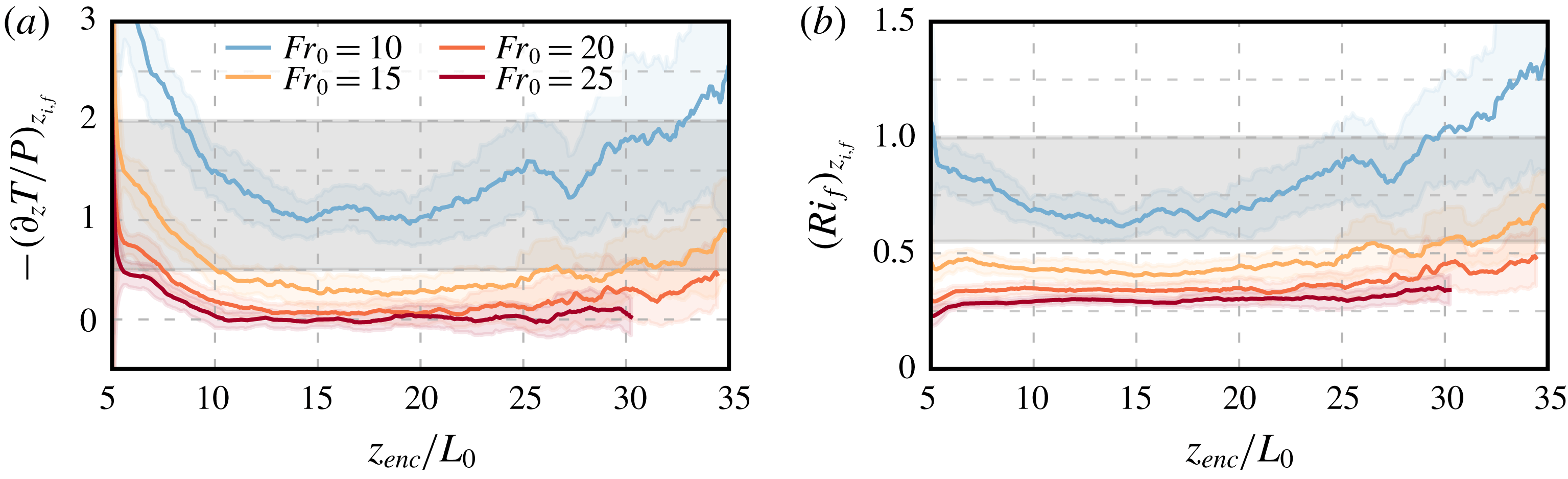
Figure 8. Temporal evolution of (a) the ratio between turbulent transport and shear production of TKE, and (b) the flux Richardson number (4.1), both evaluated at the height of the minimum buoyancy flux. Grey areas indicate the interval where both shear and convection are important, as discussed in § 6.
We have seen in the previous section that wind-shear effects on entrainment-zone properties become significant when
![]() $Fr_{0}\gtrsim 10$
. This behaviour can be understood by examining the energetics in the entrainment zone. The ratio between the turbulent-transport term and the shear-production term decreases with
$Fr_{0}\gtrsim 10$
. This behaviour can be understood by examining the energetics in the entrainment zone. The ratio between the turbulent-transport term and the shear-production term decreases with
![]() $Fr_{0}$
, as shown in figure 8(a), and both terms become comparable at
$Fr_{0}$
, as shown in figure 8(a), and both terms become comparable at
![]() $Fr_{0}\simeq 10$
. Concomitantly, the flux Richardson number,
$Fr_{0}\simeq 10$
. Concomitantly, the flux Richardson number,
becomes less than 1 and asymptotically approaches
![]() $\simeq 0.25{-}0.3$
(figure 8
b). This change in energetics with increasing shear has often been documented in previous studies (Pino et al.
Reference Pino, Vilà-Guerau De Arellano and Duynkerke2003; Conzemius & Fedorovich Reference Conzemius and Fedorovich2006a
; Fedorovich & Conzemius Reference Fedorovich and Conzemius2008; Pino & Vilà-Guerau De Arellano Reference Pino and Vilà-Guerau De Arellano2008). In this section, we further rationalize this change in energetics in terms of a change in characteristic length scales in the two-layer structure of the entrainment zone.
$\simeq 0.25{-}0.3$
(figure 8
b). This change in energetics with increasing shear has often been documented in previous studies (Pino et al.
Reference Pino, Vilà-Guerau De Arellano and Duynkerke2003; Conzemius & Fedorovich Reference Conzemius and Fedorovich2006a
; Fedorovich & Conzemius Reference Fedorovich and Conzemius2008; Pino & Vilà-Guerau De Arellano Reference Pino and Vilà-Guerau De Arellano2008). In this section, we further rationalize this change in energetics in terms of a change in characteristic length scales in the two-layer structure of the entrainment zone.
4.1 The two-layer structure of the entrainment zone in the shear-free CBL
The analysis presented in this section is based on previous work on shear-free CBLs by Garcia & Mellado (Reference Garcia and Mellado2014), who described the entrainment zone as a composition of two sublayers (cf. figure 9). The lower entrainment-zone (EZ) sublayer is located around
![]() $z_{i,f}$
and is characterized by a length scale proportional to the CBL depth and by the convective scales derived from the CBL depth and the surface buoyancy flux (Deardorff Reference Deardorff1970). The scaling law for
$z_{i,f}$
and is characterized by a length scale proportional to the CBL depth and by the convective scales derived from the CBL depth and the surface buoyancy flux (Deardorff Reference Deardorff1970). The scaling law for
![]() $z_{i,f}$
in shear-free CBLs is (figure 10
a)
$z_{i,f}$
in shear-free CBLs is (figure 10
a)
On the left-hand side, we measure distances with respect to
![]() $z_{enc}$
, the encroachment length scale, because
$z_{enc}$
, the encroachment length scale, because
![]() $z_{enc}$
provides an analytical reference height for the position of the entrainment zone, and subtracting this order-of-one quantity allows us to emphasize the local structure. (By ‘scaling law’ we mean functional relationships between dependent and independent variables that are consistent with the dimensional analysis presented in § 2.2.)
$z_{enc}$
provides an analytical reference height for the position of the entrainment zone, and subtracting this order-of-one quantity allows us to emphasize the local structure. (By ‘scaling law’ we mean functional relationships between dependent and independent variables that are consistent with the dimensional analysis presented in § 2.2.)
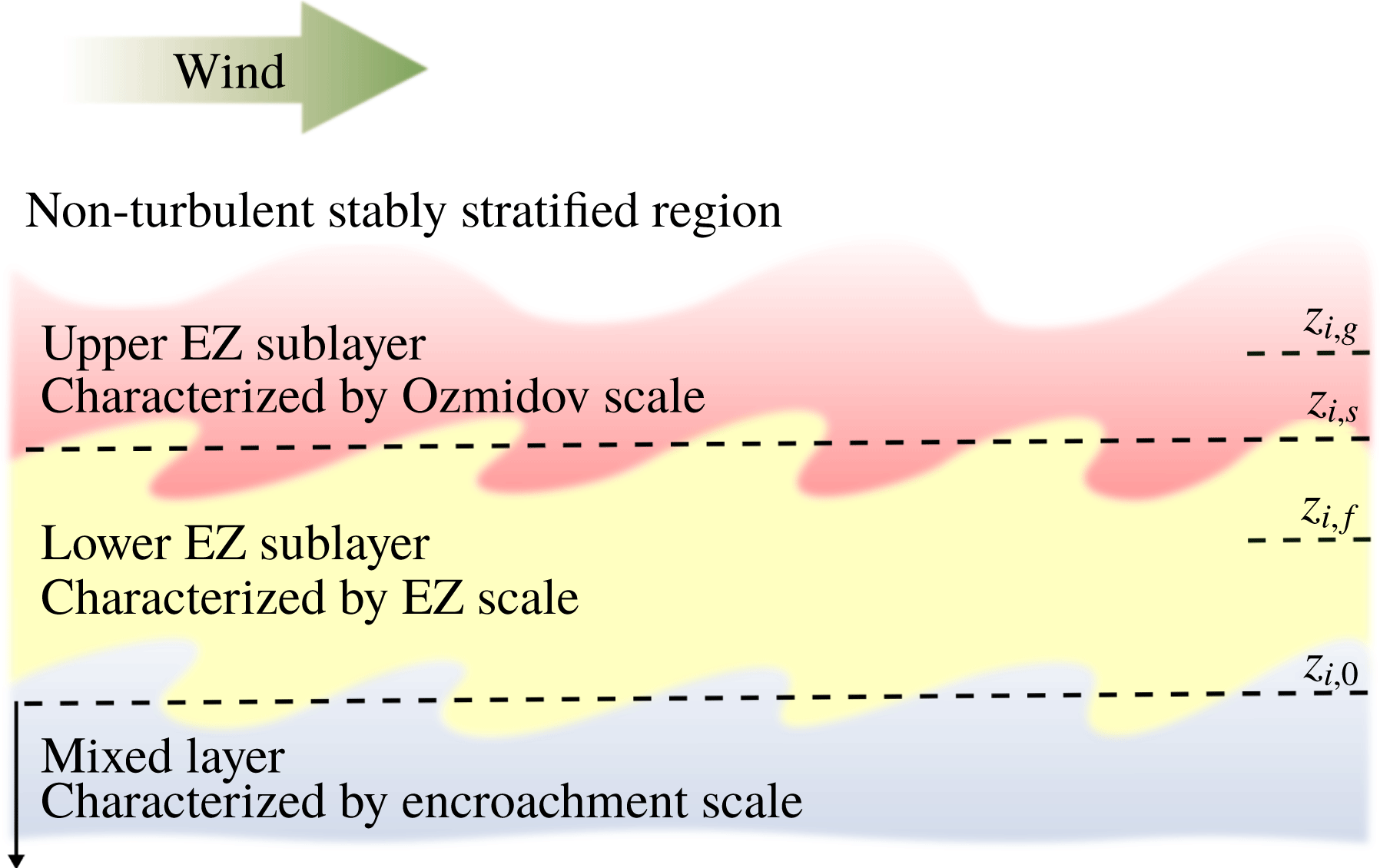
Figure 9. Sketch of the vertical structure of the CBL-top region. Here
![]() $z_{i,0}$
is the zero-crossing height;
$z_{i,0}$
is the zero-crossing height;
![]() $z_{i,f}$
is the height of the minimum buoyancy flux;
$z_{i,f}$
is the height of the minimum buoyancy flux;
![]() $z_{i,s}$
marks the transition from the lower EZ sublayer to the upper EZ sublayer; and
$z_{i,s}$
marks the transition from the lower EZ sublayer to the upper EZ sublayer; and
![]() $z_{i,g}$
is the height of the maximum buoyancy gradient. Red indicates the upper EZ sublayer, yellow indicates the lower EZ sublayer, and blue indicates the mixed layer.
$z_{i,g}$
is the height of the maximum buoyancy gradient. Red indicates the upper EZ sublayer, yellow indicates the lower EZ sublayer, and blue indicates the mixed layer.
The upper EZ sublayer is centred around
![]() $z_{i,g}$
, acts as a transition layer between the turbulent region below and the non-turbulent stably stratified region above, and is characterized by local scales. The local length scale is
$z_{i,g}$
, acts as a transition layer between the turbulent region below and the non-turbulent stably stratified region above, and is characterized by local scales. The local length scale is
![]() $(L_{Oz})_{z_{i,f}}$
, the Ozmidov scale defined in (2.5) particularized at the height of the minimum buoyancy flux
$(L_{Oz})_{z_{i,f}}$
, the Ozmidov scale defined in (2.5) particularized at the height of the minimum buoyancy flux
![]() $z_{i,f}$
. Since the upper EZ sublayer, which is characterized by
$z_{i,f}$
. Since the upper EZ sublayer, which is characterized by
![]() $(L_{Oz})_{z_{i,f}}$
, is on top of the lower EZ sublayer, which is characterized by
$(L_{Oz})_{z_{i,f}}$
, is on top of the lower EZ sublayer, which is characterized by
![]() $z_{enc}$
, we seek a scaling law for
$z_{enc}$
, we seek a scaling law for
![]() $z_{i,g}$
of the form
$z_{i,g}$
of the form
where
![]() $\unicode[STIX]{x1D6FC}_{c}$
and
$\unicode[STIX]{x1D6FC}_{c}$
and
![]() $\unicode[STIX]{x1D6FD}_{c}$
are constants to be determined. This ansatz is supported by figure 10(b). A linear regression to the data for
$\unicode[STIX]{x1D6FD}_{c}$
are constants to be determined. This ansatz is supported by figure 10(b). A linear regression to the data for
![]() $z_{enc}/L_{0}\gtrsim 15$
provides the values
$z_{enc}/L_{0}\gtrsim 15$
provides the values
![]() $\unicode[STIX]{x1D6FC}_{c}=0.184$
and
$\unicode[STIX]{x1D6FC}_{c}=0.184$
and
![]() $\unicode[STIX]{x1D6FD}_{c}=1.78$
. Equation (4.3) extends the result
$\unicode[STIX]{x1D6FD}_{c}=1.78$
. Equation (4.3) extends the result
![]() $z_{i,g}\propto z_{enc}$
proposed in Garcia & Mellado (Reference Garcia and Mellado2014) with a first-order correction proportional to
$z_{i,g}\propto z_{enc}$
proposed in Garcia & Mellado (Reference Garcia and Mellado2014) with a first-order correction proportional to
![]() $(L_{Oz})_{z_{i,f}}$
.
$(L_{Oz})_{z_{i,f}}$
.
We can define
as a reference height that marks the transition from the lower EZ sublayer to the upper EZ sublayer, i.e. the transition from a region characterized by
![]() $z_{enc}$
to a region characterized by
$z_{enc}$
to a region characterized by
![]() $(L_{Oz})_{z_{i,f}}$
. The upper boundary of the entrainment zone, and thus the upper boundary of the CBL, can be estimated as
$(L_{Oz})_{z_{i,f}}$
. The upper boundary of the entrainment zone, and thus the upper boundary of the CBL, can be estimated as
![]() $z_{i,g}+1.78(L_{Oz})_{z_{i,f}}$
. The thickness of the upper EZ sublayer can be estimated as
$z_{i,g}+1.78(L_{Oz})_{z_{i,f}}$
. The thickness of the upper EZ sublayer can be estimated as
![]() $2(z_{i,g}-z_{i,s})\simeq 3.56(L_{Oz})_{z_{i,f}}$
. As later discussed in § 5, the length scale
$2(z_{i,g}-z_{i,s})\simeq 3.56(L_{Oz})_{z_{i,f}}$
. As later discussed in § 5, the length scale
![]() $(L_{Oz})_{z_{i,f}}$
varies only weakly in time and it is well approximated by
$(L_{Oz})_{z_{i,f}}$
varies only weakly in time and it is well approximated by
![]() $0.45L_{0}$
, where
$0.45L_{0}$
, where
![]() $L_{0}$
is the reference Ozmidov length.
$L_{0}$
is the reference Ozmidov length.
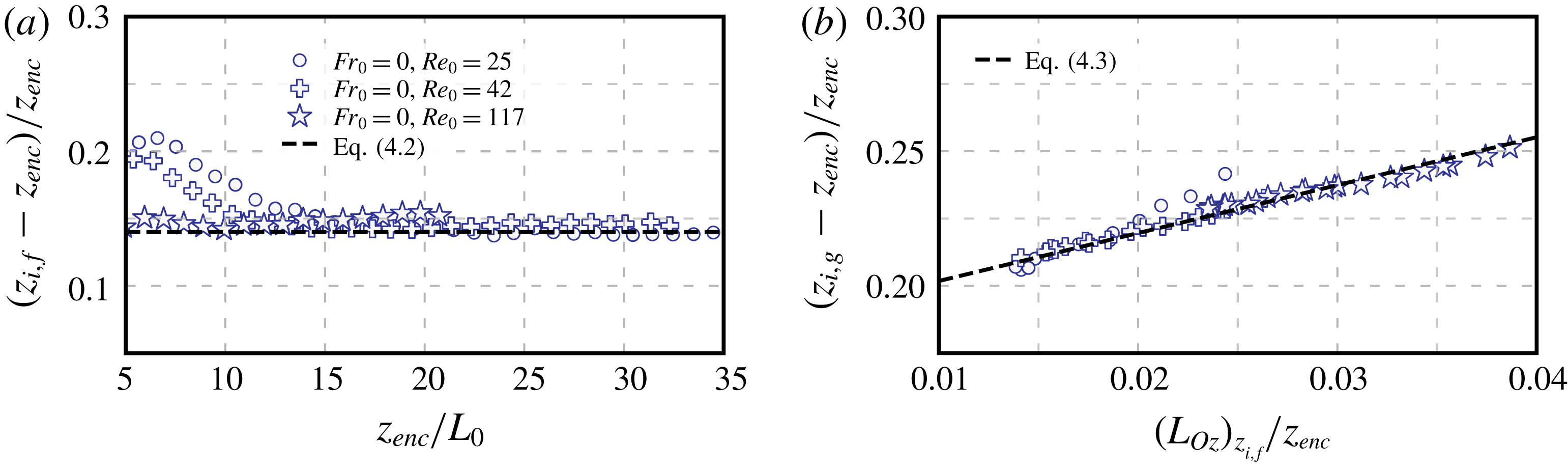
Figure 10. Scaling of the flux-based and gradient-based CBL depths in the shear-free CBL in terms of the encroachment length,
![]() $z_{enc}$
, and the Ozmidov length
$z_{enc}$
, and the Ozmidov length
![]() $(L_{Oz})_{z_{i,f}}$
. Symbols indicate the average within an interval
$(L_{Oz})_{z_{i,f}}$
. Symbols indicate the average within an interval
![]() $\unicode[STIX]{x0394}z_{enc}/L_{0}=2$
. In panel (b), only data for
$\unicode[STIX]{x0394}z_{enc}/L_{0}=2$
. In panel (b), only data for
![]() $z_{enc}/L_{0}\gtrsim 15$
are considered.
$z_{enc}/L_{0}\gtrsim 15$
are considered.
4.2 The two-layer structure of the entrainment zone in the sheared CBL
How does the two-layer structure of the entrainment zone change with wind in the free atmosphere? As observed in § 3, wind in the free atmosphere leads to the formation of a shear layer in the entrainment zone, i.e. a layer of marked variation of the mean velocity between two regions with homogeneous velocity. From the various idealized configurations often employed to study stably stratified sheared turbulence, the stably stratified shear layer seems appropriate to introduce the discussion on the interaction between shear and stratification in the entrainment zone of the CBL, given the coincidence of a localized shear layer with a localized stratified layer (see e.g. Sherman, Imberger & Corcos Reference Sherman, Imberger and Corcos1978; Peltier & Caulfield Reference Peltier and Caulfield2003; Mashayek & Peltier Reference Mashayek and Peltier2011). The minimum gradient Richardson number
is a major variable characterizing the evolution of stably stratified shear layers. If the initial shear layer is thin enough for the Richardson number to be relatively small, Kelvin–Helmholtz-like instabilities will cause an overturning of the stably stratified fluid and a thickening of the shear layer. As the shear layer thickens, overturning the fluid becomes more difficult because the vertical displacement increases whereas the available kinetic energy, proportional to the squared velocity jump across the shear layer, remains constant. Once the shear layer reaches a critical thickness, or equivalently a critical Richardson number, the available kinetic energy is insufficient to overturn the fluid and turbulence decays. Results show that this critical Richardson number is
![]() $1/3\pm 15\,\%$
, the uncertainty interval representing statistical convergence and the dependence on Prandtl number, Reynolds number and initial conditions given that the flow is strongly transient (see e.g. Smyth & Moum Reference Smyth and Moum2000b
; Brucker & Sarkar Reference Brucker and Sarkar2007; Howland, Taylor & Caulfield Reference Howland, Taylor and Caulfield2018).
$1/3\pm 15\,\%$
, the uncertainty interval representing statistical convergence and the dependence on Prandtl number, Reynolds number and initial conditions given that the flow is strongly transient (see e.g. Smyth & Moum Reference Smyth and Moum2000b
; Brucker & Sarkar Reference Brucker and Sarkar2007; Howland, Taylor & Caulfield Reference Howland, Taylor and Caulfield2018).
In the CBL, convection in the mixed layer underneath the entrainment zone is expected to introduce important differences with respect to the stably stratified shear layer. One difference is that turbulence is sustained for a gradient Richardson number significantly larger than
![]() $1/3$
. This is shown in figure 11(a), which plots
$1/3$
. This is shown in figure 11(a), which plots
![]() $Ri_{g}$
at the height of the minimum buoyancy flux, which approximately coincides with the height of the minimum
$Ri_{g}$
at the height of the minimum buoyancy flux, which approximately coincides with the height of the minimum
![]() $Ri_{g}$
. The main reason is that convective motions in the CBL make the shear layer locally thinner, which leads to local subcritical Richardson numbers and hence local shear instabilities that maintain a turbulent state (Mahrt & Lenschow Reference Mahrt and Lenschow1976; Kim et al.
Reference Kim, Park and Moeng2003; Conzemius & Fedorovich Reference Conzemius and Fedorovich2007). It is curious that the gradient Richardson number in the entrainment zone approaches the value
$Ri_{g}$
. The main reason is that convective motions in the CBL make the shear layer locally thinner, which leads to local subcritical Richardson numbers and hence local shear instabilities that maintain a turbulent state (Mahrt & Lenschow Reference Mahrt and Lenschow1976; Kim et al.
Reference Kim, Park and Moeng2003; Conzemius & Fedorovich Reference Conzemius and Fedorovich2007). It is curious that the gradient Richardson number in the entrainment zone approaches the value
![]() $1/3$
as shear increases, which is the upper value observed in stably stratified shear layers, although there is a priori no strong argument to expect this agreement given the strong differences between the two cases.
$1/3$
as shear increases, which is the upper value observed in stably stratified shear layers, although there is a priori no strong argument to expect this agreement given the strong differences between the two cases.
To quantify how wind shear modifies the lower EZ sublayer, specifically, the scaling law (4.2) for
![]() $z_{i,f}$
, we introduce the length scale
$z_{i,f}$
, we introduce the length scale
where
is the velocity difference across the entrainment zone, the mixed-layer value
![]() $u_{ml}$
being defined by (3.3). The length scale
$u_{ml}$
being defined by (3.3). The length scale
![]() $\unicode[STIX]{x0394}z_{i}$
is referred to as the vorticity thickness in the literature of stably stratified shear layers. In this work we will refer to
$\unicode[STIX]{x0394}z_{i}$
is referred to as the vorticity thickness in the literature of stably stratified shear layers. In this work we will refer to
![]() $\unicode[STIX]{x0394}z_{i}$
as the EZ scale, because, as shown in the remainder of this section and in § 5,
$\unicode[STIX]{x0394}z_{i}$
as the EZ scale, because, as shown in the remainder of this section and in § 5,
![]() $\unicode[STIX]{x0394}z_{i}$
characterizes the lower EZ sublayer (cf. figure 9). Since the lower EZ sublayer is on top of the mixed layer, which is characterized by
$\unicode[STIX]{x0394}z_{i}$
characterizes the lower EZ sublayer (cf. figure 9). Since the lower EZ sublayer is on top of the mixed layer, which is characterized by
![]() $z_{enc}$
, we seek a scaling law for
$z_{enc}$
, we seek a scaling law for
![]() $z_{i,f}$
that is a linear combination of
$z_{i,f}$
that is a linear combination of
![]() $\unicode[STIX]{x0394}z_{i}$
and
$\unicode[STIX]{x0394}z_{i}$
and
![]() $z_{enc}$
. Figure 12(a) supports this ansatz, and a linear regression to the data for
$z_{enc}$
. Figure 12(a) supports this ansatz, and a linear regression to the data for
![]() $z_{enc}/L_{0}\gtrsim 15$
yields
$z_{enc}/L_{0}\gtrsim 15$
yields
The largest deviation from this linear behaviour occurs for weak wind conditions,
![]() $Fr_{0}\lesssim 10$
, where the turbulent and buoyancy Reynolds numbers in the entrainment zone are smallest in our DNS (see table 1). However, even in these cases, the linear behaviour is approached as the CBL – and accordingly the Reynolds number – grows, the deviation becoming less than 20 % for
$Fr_{0}\lesssim 10$
, where the turbulent and buoyancy Reynolds numbers in the entrainment zone are smallest in our DNS (see table 1). However, even in these cases, the linear behaviour is approached as the CBL – and accordingly the Reynolds number – grows, the deviation becoming less than 20 % for
![]() $z_{enc}/L_{0}\gtrsim 25$
. The data from the case
$z_{enc}/L_{0}\gtrsim 25$
. The data from the case
![]() $Fr_{0}=10$
and
$Fr_{0}=10$
and
![]() $Re_{0}=42$
further support this argument, since the deviation of these data from (4.8) at
$Re_{0}=42$
further support this argument, since the deviation of these data from (4.8) at
![]() $z_{enc}/L_{0}=15$
decreases by
$z_{enc}/L_{0}=15$
decreases by
![]() $\simeq 33\,\%$
with respect to the case
$\simeq 33\,\%$
with respect to the case
![]() $Fr_{0}=10$
and
$Fr_{0}=10$
and
![]() $Re_{0}=25$
. To avoid this low-Reynolds-number effect from the weak shear cases, only the data from the cases
$Re_{0}=25$
. To avoid this low-Reynolds-number effect from the weak shear cases, only the data from the cases
![]() $Fr_{0}>10$
are considered in the regression. Last, we also verified that the dependence of the regression coefficients on the threshold of
$Fr_{0}>10$
are considered in the regression. Last, we also verified that the dependence of the regression coefficients on the threshold of
![]() $z_{enc}/L_{0}$
is small: the coefficients in
$z_{enc}/L_{0}$
is small: the coefficients in
![]() $z_{i,f}\simeq 0.94z_{enc}+0.8\unicode[STIX]{x0394}z_{i}$
vary by
$z_{i,f}\simeq 0.94z_{enc}+0.8\unicode[STIX]{x0394}z_{i}$
vary by
![]() $\simeq 2\,\%$
and
$\simeq 2\,\%$
and
![]() $\simeq 5\,\%$
, respectively, as the threshold changes from
$\simeq 5\,\%$
, respectively, as the threshold changes from
![]() $15$
to
$15$
to
![]() $20$
.
$20$
.

Figure 12. Scaling of the flux-based and gradient-based CBL depths in the sheared CBL in terms of the encroachment length
![]() $z_{enc}$
, the EZ scale
$z_{enc}$
, the EZ scale
![]() $\unicode[STIX]{x0394}z_{i}$
, and the Ozmidov length
$\unicode[STIX]{x0394}z_{i}$
, and the Ozmidov length
![]() $(L_{Oz})_{z_{i,f}}$
. Light colours indicate low values of
$(L_{Oz})_{z_{i,f}}$
. Light colours indicate low values of
![]() $z_{enc}/L_{0}$
, and dark colours indicate higher values of
$z_{enc}/L_{0}$
, and dark colours indicate higher values of
![]() $z_{enc}/L_{0}$
.
$z_{enc}/L_{0}$
.
We can easily find the limits of
![]() $\unicode[STIX]{x0394}z_{i}$
for weak wind conditions and strong wind conditions. For a vanishingly small wind, (4.8) has to recover (4.2), which implies that we can define
$\unicode[STIX]{x0394}z_{i}$
for weak wind conditions and strong wind conditions. For a vanishingly small wind, (4.8) has to recover (4.2), which implies that we can define
as the asymptotic limit of
![]() $\unicode[STIX]{x0394}z_{i}$
when
$\unicode[STIX]{x0394}z_{i}$
when
![]() $Fr_{0}$
tends towards zero. This limit is indicated in figure 12(a) by the bold
$Fr_{0}$
tends towards zero. This limit is indicated in figure 12(a) by the bold
![]() $\times$
symbol. We will refer to
$\times$
symbol. We will refer to
![]() $(\unicode[STIX]{x0394}z_{i})_{c}$
as the convective limit of the EZ scale. To obtain the behaviour of
$(\unicode[STIX]{x0394}z_{i})_{c}$
as the convective limit of the EZ scale. To obtain the behaviour of
![]() $\unicode[STIX]{x0394}z_{i}$
for a strong wind, we use (4.5) to rewrite (4.6) as
$\unicode[STIX]{x0394}z_{i}$
for a strong wind, we use (4.5) to rewrite (4.6) as
![]() $\unicode[STIX]{x0394}z_{i}\simeq \sqrt{(Ri_{g})_{z_{i,f}}}\unicode[STIX]{x0394}u/N_{0}$
, where we have used the result
$\unicode[STIX]{x0394}z_{i}\simeq \sqrt{(Ri_{g})_{z_{i,f}}}\unicode[STIX]{x0394}u/N_{0}$
, where we have used the result
![]() $(\unicode[STIX]{x2202}_{z}\langle b\rangle )_{z_{i,f}}\simeq N_{0}^{2}$
shown in figure 11(b). Hence, as the wind strength increases and the gradient Richardson number decreases towards
$(\unicode[STIX]{x2202}_{z}\langle b\rangle )_{z_{i,f}}\simeq N_{0}^{2}$
shown in figure 11(b). Hence, as the wind strength increases and the gradient Richardson number decreases towards
![]() $1/3$
,
$1/3$
,
![]() $\unicode[STIX]{x0394}z_{i}$
asymptotically approaches
$\unicode[STIX]{x0394}z_{i}$
asymptotically approaches
We will refer to
![]() $(\unicode[STIX]{x0394}z_{i})_{s}$
as the shear limit of the EZ scale. When convection dominates in the entrainment zone,
$(\unicode[STIX]{x0394}z_{i})_{s}$
as the shear limit of the EZ scale. When convection dominates in the entrainment zone,
![]() $(\unicode[STIX]{x0394}z_{i})_{s}$
is smaller than
$(\unicode[STIX]{x0394}z_{i})_{s}$
is smaller than
![]() $(\unicode[STIX]{x0394}z_{i})_{c}$
, and the latter characterizes the lower EZ sublayer. As the wind intensity
$(\unicode[STIX]{x0394}z_{i})_{c}$
, and the latter characterizes the lower EZ sublayer. As the wind intensity
![]() $U_{0}$
increases,
$U_{0}$
increases,
![]() $(\unicode[STIX]{x0394}z_{i})_{s}$
increases and eventually becomes comparable to
$(\unicode[STIX]{x0394}z_{i})_{s}$
increases and eventually becomes comparable to
![]() $(\unicode[STIX]{x0394}z_{i})_{c}$
, at which point
$(\unicode[STIX]{x0394}z_{i})_{c}$
, at which point
![]() $(\unicode[STIX]{x0394}z_{i})_{s}$
starts to characterize the lower EZ sublayer. The weakly to strongly unstable conditions
$(\unicode[STIX]{x0394}z_{i})_{s}$
starts to characterize the lower EZ sublayer. The weakly to strongly unstable conditions
![]() $-z_{enc}/L_{Ob}\gtrsim 4$
considered in this paper correspond to
$-z_{enc}/L_{Ob}\gtrsim 4$
considered in this paper correspond to
![]() $(\unicode[STIX]{x0394}z_{i})_{s}/(\unicode[STIX]{x0394}z_{i})_{c}\lesssim 1.5$
. We will further explore in § 5 the capability of the ratio
$(\unicode[STIX]{x0394}z_{i})_{s}/(\unicode[STIX]{x0394}z_{i})_{c}\lesssim 1.5$
. We will further explore in § 5 the capability of the ratio
![]() $(\unicode[STIX]{x0394}z_{i})_{s}/(\unicode[STIX]{x0394}z_{i})_{c}$
to characterize shear effects on entrainment-zone properties.
$(\unicode[STIX]{x0394}z_{i})_{s}/(\unicode[STIX]{x0394}z_{i})_{c}$
to characterize shear effects on entrainment-zone properties.
To characterize the upper EZ sublayer, we propose the following scaling law for the height of the maximum buoyancy gradient:
This ansatz is motivated by (4.3), which indicates that, for shear-free conditions, the position of the upper EZ sublayer with respect to the lower EZ sublayer can be characterized by a linear combination of the scales characterizing the lower and upper sublayers. Figure 12(b) supports this ansatz, providing the coefficients
![]() $\unicode[STIX]{x1D6FE}_{s}\simeq 0.184$
and
$\unicode[STIX]{x1D6FE}_{s}\simeq 0.184$
and
![]() $\unicode[STIX]{x1D6FD}_{s}\simeq 1.78$
. The linear behaviour is also supported by the data corresponding to higher Reynolds-number simulations (
$\unicode[STIX]{x1D6FD}_{s}\simeq 1.78$
. The linear behaviour is also supported by the data corresponding to higher Reynolds-number simulations (
![]() $Re_{0}=42$
), although longer simulations would help to further validate (4.11). For vanishingly small
$Re_{0}=42$
), although longer simulations would help to further validate (4.11). For vanishingly small
![]() $Fr_{0}$
, substituting
$Fr_{0}$
, substituting
![]() $\unicode[STIX]{x0394}z_{i}$
by
$\unicode[STIX]{x0394}z_{i}$
by
![]() $(\unicode[STIX]{x0394}z_{i})_{c}$
in (4.8) and (4.11) recovers the shear-free result (4.3), which indicates that changes in the upper EZ sublayer due to wind shear are captured by the changes in
$(\unicode[STIX]{x0394}z_{i})_{c}$
in (4.8) and (4.11) recovers the shear-free result (4.3), which indicates that changes in the upper EZ sublayer due to wind shear are captured by the changes in
![]() $(L_{Oz})_{z_{i,f}}$
, the Ozmidov scale at
$(L_{Oz})_{z_{i,f}}$
, the Ozmidov scale at
![]() $z_{i,f}$
. This further supports this length as a characteristic scale of the upper EZ sublayer. As the turbulence intensity in the lower EZ sublayer increases with respect to shear-free conditions, the lower EZ sublayer broadens and so does the upper EZ sublayer.
$z_{i,f}$
. This further supports this length as a characteristic scale of the upper EZ sublayer. As the turbulence intensity in the lower EZ sublayer increases with respect to shear-free conditions, the lower EZ sublayer broadens and so does the upper EZ sublayer.
In summary, the entrainment zone in sheared CBLs can also be described as a composition of two sublayers, the lower EZ sublayer around the height of the minimum buoyancy flux, and the upper EZ sublayer around the height of the maximum buoyancy gradient. The difference from the shear-free case is that wind introduces a local scale
![]() $\unicode[STIX]{x0394}z_{i}$
in the characterization of the entrainment zone, in addition to the encroachment scale
$\unicode[STIX]{x0394}z_{i}$
in the characterization of the entrainment zone, in addition to the encroachment scale
![]() $z_{enc}$
and the Ozmidov scale
$z_{enc}$
and the Ozmidov scale
![]() $(L_{Oz})_{z_{i,f}}$
. The scaling laws for the reference heights are:
$(L_{Oz})_{z_{i,f}}$
. The scaling laws for the reference heights are:
5 Quantifying wind-shear effects on entrainment-zone properties
Normalized entrainment-zone properties in the barotropic CBLs considered in this study depend on the Froude number
![]() $Fr_{0}$
and on the normalized CBL depth
$Fr_{0}$
and on the normalized CBL depth
![]() $z_{enc}/L_{0}$
. The analysis of the entrainment-zone structure presented in § 4, however, indicates that the variable
$z_{enc}/L_{0}$
. The analysis of the entrainment-zone structure presented in § 4, however, indicates that the variable
![]() $\unicode[STIX]{x0394}z_{i}/z_{enc}$
embeds both dependences and fully describes key properties such as
$\unicode[STIX]{x0394}z_{i}/z_{enc}$
embeds both dependences and fully describes key properties such as
![]() $z_{i,f}$
. This reduction from two independent variables to one independent variable can help simplify the parametrization of wind-shear effects in boundary-layer schemes of atmospheric models. Therefore, we further investigate in this section the capability of the EZ scale,
$z_{i,f}$
. This reduction from two independent variables to one independent variable can help simplify the parametrization of wind-shear effects in boundary-layer schemes of atmospheric models. Therefore, we further investigate in this section the capability of the EZ scale,
![]() $\unicode[STIX]{x0394}z_{i}$
, to characterize entrainment-zone properties. Moreover, we will obtain a relationship between
$\unicode[STIX]{x0394}z_{i}$
, to characterize entrainment-zone properties. Moreover, we will obtain a relationship between
![]() $\unicode[STIX]{x0394}z_{i}$
and the velocity increment across the entrainment zone,
$\unicode[STIX]{x0394}z_{i}$
and the velocity increment across the entrainment zone,
![]() $\unicode[STIX]{x0394}u$
, so that the latter can be used as independent variable. The motivation for changing the variable
$\unicode[STIX]{x0394}u$
, so that the latter can be used as independent variable. The motivation for changing the variable
![]() $\unicode[STIX]{x0394}z_{i}$
by the variable
$\unicode[STIX]{x0394}z_{i}$
by the variable
![]() $\unicode[STIX]{x0394}u$
is that
$\unicode[STIX]{x0394}u$
is that
![]() $\unicode[STIX]{x0394}z_{i}$
is locally defined in terms of a gradient (cf. (4.6)) whereas
$\unicode[STIX]{x0394}z_{i}$
is locally defined in terms of a gradient (cf. (4.6)) whereas
![]() $\unicode[STIX]{x0394}u$
is defined as the velocity difference between two regions of homogeneous velocity (cf. (4.7)), and thus
$\unicode[STIX]{x0394}u$
is defined as the velocity difference between two regions of homogeneous velocity (cf. (4.7)), and thus
![]() $\unicode[STIX]{x0394}u$
is less sensitive to measurements and numerical uncertainties.
$\unicode[STIX]{x0394}u$
is less sensitive to measurements and numerical uncertainties.
5.1 Scaling law for the EZ scale,
 $\unicode[STIX]{x0394}z_{i}$
$\unicode[STIX]{x0394}z_{i}$
To derive a scaling law for
![]() $\unicode[STIX]{x0394}z_{i}$
, we consider the integral analysis of the TKE balance equation discussed in § 2.4 but restricted to the entrainment zone:
$\unicode[STIX]{x0394}z_{i}$
, we consider the integral analysis of the TKE balance equation discussed in § 2.4 but restricted to the entrainment zone:
Henceforth, the superscript
![]() $EZ$
stands for entrainment zone and indicates that the corresponding integral is calculated in the interval
$EZ$
stands for entrainment zone and indicates that the corresponding integral is calculated in the interval
![]() $z_{i,0}<z<z_{\infty }$
. To better quantify shear effects, we subtract the balance equation for the shear-free CBL from the balance equation for the sheared CBL, and we focus on the cases
$z_{i,0}<z<z_{\infty }$
. To better quantify shear effects, we subtract the balance equation for the shear-free CBL from the balance equation for the sheared CBL, and we focus on the cases
![]() $Fr_{0}\gtrsim 15$
because wind-shear effects on entrainment-zone properties are small for smaller Froude numbers.
$Fr_{0}\gtrsim 15$
because wind-shear effects on entrainment-zone properties are small for smaller Froude numbers.
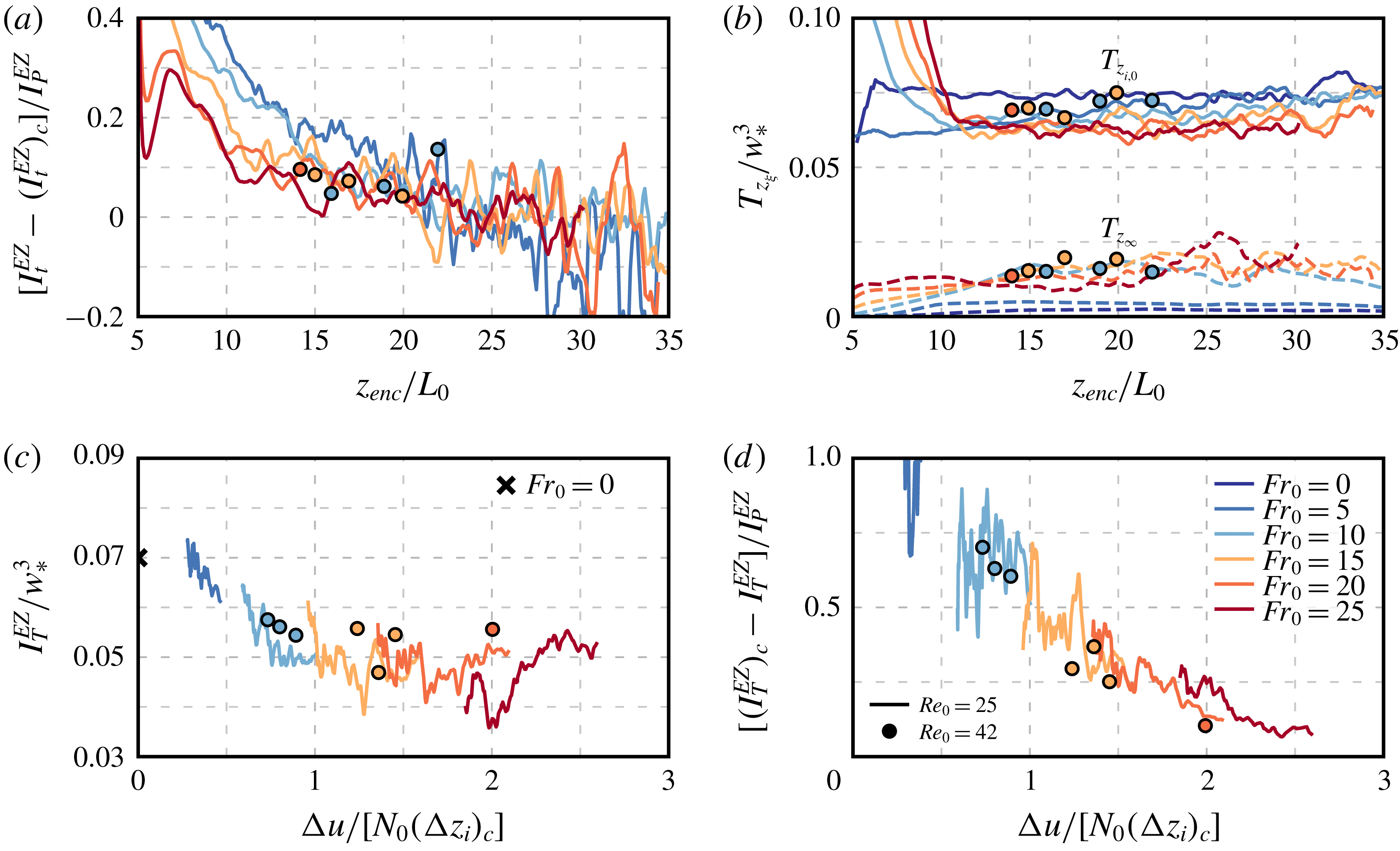
Figure 13. Temporal evolution of the contributions from the accumulation term,
![]() $I_{t}^{EZ}$
, and the turbulent-transport term,
$I_{t}^{EZ}$
, and the turbulent-transport term,
![]() $I_{T}^{EZ}=T_{z_{i,0}}-T_{z_{\infty }}$
, to the TKE budget equation (5.1). The subscript
$I_{T}^{EZ}=T_{z_{i,0}}-T_{z_{\infty }}$
, to the TKE budget equation (5.1). The subscript
![]() $c$
indicates the convective limit
$c$
indicates the convective limit
![]() $Fr_{0}=0$
.
$Fr_{0}=0$
.
The shear enhancement of the accumulation term on the left-hand side of (5.1) is less than 10–20 % of the shear-production term for
![]() $z_{enc}/L_{0}\gtrsim 15$
(cf. figure 13
a) and hence negligible to leading order, which indicates a quasi-steady regime in the entrainment zone. The transport term can be written as
$z_{enc}/L_{0}\gtrsim 15$
(cf. figure 13
a) and hence negligible to leading order, which indicates a quasi-steady regime in the entrainment zone. The transport term can be written as
i.e. the difference between the transport of kinetic energy from the mixed layer into the entrainment zone and the transport of kinetic energy from the entrainment zone into the free atmosphere. As seen in figure 13(b), shear reduces the energy that is transported into the entrainment zone from the mixed layer and shear increases the energy that is radiated out into the free atmosphere by gravity waves, so that
![]() $I_{T}^{EZ}$
decreases with increasing shear. For weak shear conditions
$I_{T}^{EZ}$
decreases with increasing shear. For weak shear conditions
![]() $Fr_{0}=5$
, the reduction of energy transported into the entrainment zone is larger than the enhancement of energy drained at the top (cf. figure 13
b), which suggests that shear sheltering (Hunt & Durbin Reference Hunt and Durbin1999) dominates over shear enhancement of gravity-wave radiation (Schröter Reference Schröter2018). This effect on the transport term for weak shear conditions, however, is not observed in the entrainment flux and viscous dissipation rate, which remain practically unchanged for
$Fr_{0}=5$
, the reduction of energy transported into the entrainment zone is larger than the enhancement of energy drained at the top (cf. figure 13
b), which suggests that shear sheltering (Hunt & Durbin Reference Hunt and Durbin1999) dominates over shear enhancement of gravity-wave radiation (Schröter Reference Schröter2018). This effect on the transport term for weak shear conditions, however, is not observed in the entrainment flux and viscous dissipation rate, which remain practically unchanged for
![]() $Fr_{0}\lesssim 10$
once the CBL is inside the quasi-steady regime (see also figures 5
a and 7
a). We also see that the shear reduction of
$Fr_{0}\lesssim 10$
once the CBL is inside the quasi-steady regime (see also figures 5
a and 7
a). We also see that the shear reduction of
![]() $I_{T}^{EZ}$
saturates and asymptotically approaches
$I_{T}^{EZ}$
saturates and asymptotically approaches
![]() $\simeq 0.02w_{\ast }^{3}$
with increasing shear, where
$\simeq 0.02w_{\ast }^{3}$
with increasing shear, where
![]() $w_{\ast }^{3}=B_{0}z_{enc}$
. This saturation is more clearly shown in figure 13(c), where we plot the flux difference across the entrainment zone as a function of the variable
$w_{\ast }^{3}=B_{0}z_{enc}$
. This saturation is more clearly shown in figure 13(c), where we plot the flux difference across the entrainment zone as a function of the variable
![]() $\unicode[STIX]{x0394}u/[N_{0}(\unicode[STIX]{x0394}z_{i})_{c}]$
. (Using this independent variable is motivated by the results presented below.) Hence, as the shear production increases, the relative contribution of the turbulent transport in (5.1) decreases (cf. figure 13
d). For instance, the relative contribution is
$\unicode[STIX]{x0394}u/[N_{0}(\unicode[STIX]{x0394}z_{i})_{c}]$
. (Using this independent variable is motivated by the results presented below.) Hence, as the shear production increases, the relative contribution of the turbulent transport in (5.1) decreases (cf. figure 13
d). For instance, the relative contribution is
![]() $\simeq 0.35I_{P}^{EZ}$
for
$\simeq 0.35I_{P}^{EZ}$
for
![]() $Fr_{0}=15$
and
$Fr_{0}=15$
and
![]() $\simeq 0.15I_{P}^{EZ}$
for
$\simeq 0.15I_{P}^{EZ}$
for
![]() $Fr_{0}=25$
. We also observe that data from cases with
$Fr_{0}=25$
. We also observe that data from cases with
![]() $Re_{0}=42$
coincide with data from cases with
$Re_{0}=42$
coincide with data from cases with
![]() $Re_{0}=25$
within the statistical convergence reached in our simulations. Although the relative contribution of
$Re_{0}=25$
within the statistical convergence reached in our simulations. Although the relative contribution of
![]() $I_{T}^{EZ}$
is arguably non-negligible for
$I_{T}^{EZ}$
is arguably non-negligible for
![]() $Fr_{0}=15$
, the shear effect on entrainment-zone properties is still moderate for that Froude number, and therefore we neglect the turbulent transport terms in (5.1) as a first approximation; this approximation is validated below.
$Fr_{0}=15$
, the shear effect on entrainment-zone properties is still moderate for that Froude number, and therefore we neglect the turbulent transport terms in (5.1) as a first approximation; this approximation is validated below.
Shear effects on the viscous dissipation rate and the buoyancy flux are negligible for
![]() $Fr_{0}\lesssim 10$
once the CBL is inside the quasi-steady regime. For
$Fr_{0}\lesssim 10$
once the CBL is inside the quasi-steady regime. For
![]() $Fr_{0}>10$
, figure 14(a) demonstrates that they are commensurate with each other,
$Fr_{0}>10$
, figure 14(a) demonstrates that they are commensurate with each other,
which indicates that energy destruction by viscous dissipation and by conversion to potential energy increase in a constant ratio independently of the shear strength in the equilibrium entrainment regime of the sheared CBL. The subscript
![]() $c$
indicates the convective limit
$c$
indicates the convective limit
![]() $Fr_{0}=0$
. All these considerations, namely, using (5.3) and neglecting the accumulation term and the turbulent transport term in (5.1), yield the relationship
$Fr_{0}=0$
. All these considerations, namely, using (5.3) and neglecting the accumulation term and the turbulent transport term in (5.1), yield the relationship
This relationship implies that the entrainment enhancement in sheared CBLs is due to the additional TKE generated by the wind shear in the entrainment zone.
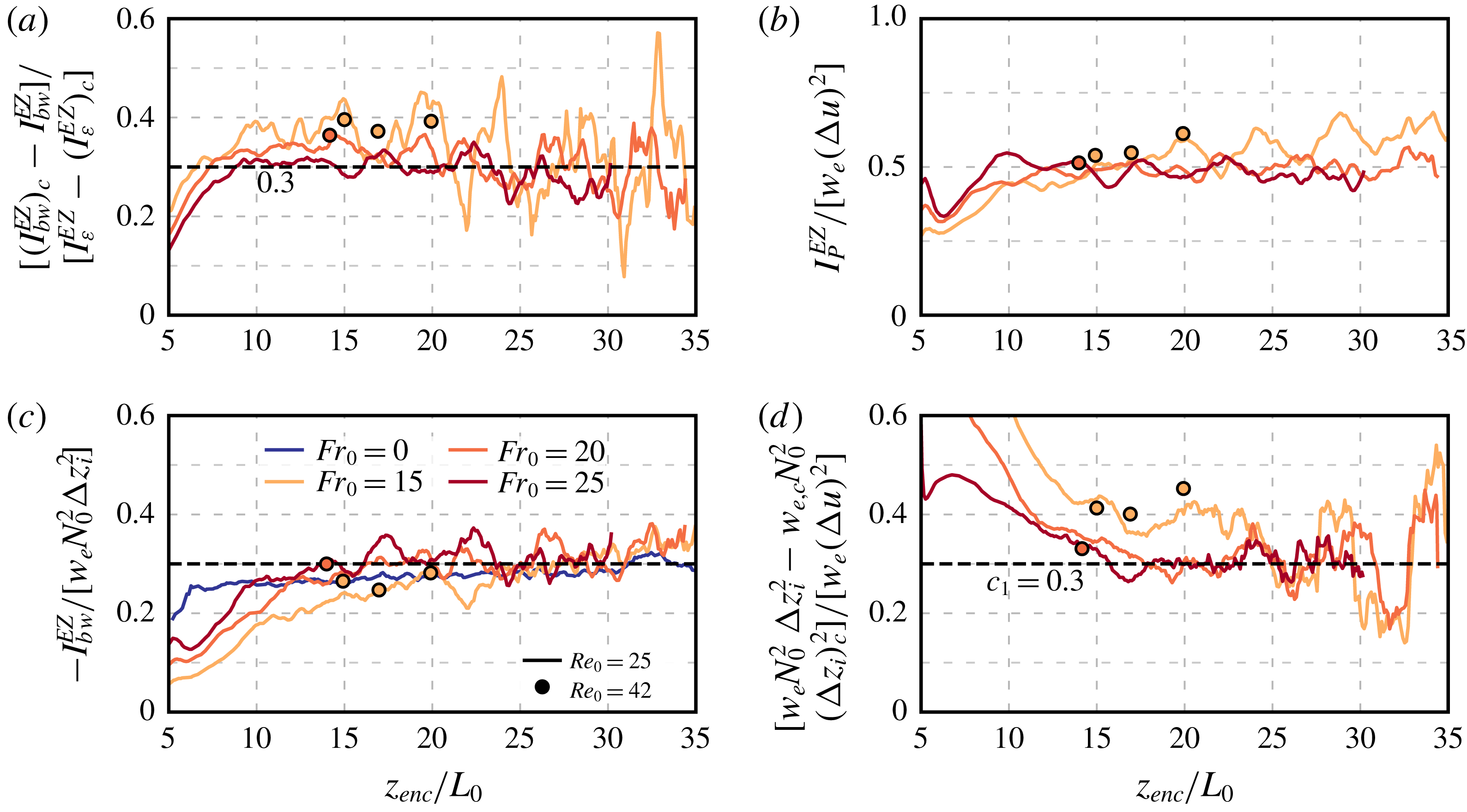
Figure 14. Scaling laws for the dominant terms in the TKE budget equation (5.1) as a function of the mean entrainment velocity,
![]() $w_{e}$
, the velocity jump across the entrainment zone,
$w_{e}$
, the velocity jump across the entrainment zone,
![]() $\unicode[STIX]{x0394}u$
, the buoyancy stratification of the free atmosphere,
$\unicode[STIX]{x0394}u$
, the buoyancy stratification of the free atmosphere,
![]() $N_{0}^{2}$
, and the EZ scale,
$N_{0}^{2}$
, and the EZ scale,
![]() $\unicode[STIX]{x0394}z_{i}$
.
$\unicode[STIX]{x0394}z_{i}$
.
Here, we proceed further and use the structure analysis presented in § 4 to estimate the terms in (5.4) and thereby obtain a closed equation for the unknown
![]() $\unicode[STIX]{x0394}z_{i}$
. First, neglecting the thickness of the upper EZ sublayer, the integration intervals in (5.4) are well approximated by
$\unicode[STIX]{x0394}z_{i}$
. First, neglecting the thickness of the upper EZ sublayer, the integration intervals in (5.4) are well approximated by
![]() $\unicode[STIX]{x0394}z_{i}$
. Second, the velocity gradient can be scaled by its maximum value,
$\unicode[STIX]{x0394}z_{i}$
. Second, the velocity gradient can be scaled by its maximum value,
![]() $\unicode[STIX]{x0394}u/\unicode[STIX]{x0394}z_{i}$
(cf. (4.6)). Last, to estimate the fluxes of buoyancy and momentum, we use the entrainment-rate equations, which are obtained by integrating the evolution equations for the mean buoyancy and mean velocity from a height
$\unicode[STIX]{x0394}u/\unicode[STIX]{x0394}z_{i}$
(cf. (4.6)). Last, to estimate the fluxes of buoyancy and momentum, we use the entrainment-rate equations, which are obtained by integrating the evolution equations for the mean buoyancy and mean velocity from a height
![]() $z_{i,f}$
upwards (see appendix A). The entrainment-rate equations provide the scalings
$z_{i,f}$
upwards (see appendix A). The entrainment-rate equations provide the scalings
![]() $-\langle b^{\prime }w^{\prime }\rangle _{z_{i,f}}\sim w_{e}\unicode[STIX]{x0394}b$
and
$-\langle b^{\prime }w^{\prime }\rangle _{z_{i,f}}\sim w_{e}\unicode[STIX]{x0394}b$
and
![]() $-\langle u^{\prime }w^{\prime }\rangle _{z_{i,f}}\sim w_{e}\unicode[STIX]{x0394}u$
. In these expressions,
$-\langle u^{\prime }w^{\prime }\rangle _{z_{i,f}}\sim w_{e}\unicode[STIX]{x0394}u$
. In these expressions,
is the mean entrainment velocity,
![]() $\unicode[STIX]{x0394}b\equiv N_{0}^{2}\unicode[STIX]{x0394}z_{i}$
is a measure of the buoyancy increment across the entrainment zone, and the velocity jump
$\unicode[STIX]{x0394}b\equiv N_{0}^{2}\unicode[STIX]{x0394}z_{i}$
is a measure of the buoyancy increment across the entrainment zone, and the velocity jump
![]() $\unicode[STIX]{x0394}u$
is defined by (4.7). All these considerations indicate that the integrals on the left-hand side and right-hand side of (5.4) are scaled by
$\unicode[STIX]{x0394}u$
is defined by (4.7). All these considerations indicate that the integrals on the left-hand side and right-hand side of (5.4) are scaled by
![]() $w_{e}\unicode[STIX]{x0394}b\unicode[STIX]{x0394}z_{i}$
and by
$w_{e}\unicode[STIX]{x0394}b\unicode[STIX]{x0394}z_{i}$
and by
![]() $w_{e}(\unicode[STIX]{x0394}u)^{2}$
, respectively, which is confirmed by figure 14(b,c). Substituting these scaling laws into (5.4) yields
$w_{e}(\unicode[STIX]{x0394}u)^{2}$
, respectively, which is confirmed by figure 14(b,c). Substituting these scaling laws into (5.4) yields
Figure 14(d) supports this ansatz and shows that
![]() $c_{1}\simeq 0.3$
. This coefficient can be interpreted as a modified Richardson number where the shear enhancement of the buoyancy flux is considered instead of the total buoyancy flux as in (4.1). This interpretation indicates that the values
$c_{1}\simeq 0.3$
. This coefficient can be interpreted as a modified Richardson number where the shear enhancement of the buoyancy flux is considered instead of the total buoyancy flux as in (4.1). This interpretation indicates that the values
![]() $(Ri_{f})_{z_{i,f}}\simeq 1$
observed when shear effects become relevant are significantly larger than the values 0.25–0.3 reported in marginally stable stratified shear flows because of the buoyancy flux caused by the turbulence in the CBL interior.
$(Ri_{f})_{z_{i,f}}\simeq 1$
observed when shear effects become relevant are significantly larger than the values 0.25–0.3 reported in marginally stable stratified shear flows because of the buoyancy flux caused by the turbulence in the CBL interior.
To use (5.6) to obtain a closed equation for the EZ scale,
![]() $\unicode[STIX]{x0394}z_{i}$
, we need to consider the mean entrainment velocity,
$\unicode[STIX]{x0394}z_{i}$
, we need to consider the mean entrainment velocity,
![]() $w_{e}$
. The shear enhancement of mean entrainment velocity,
$w_{e}$
. The shear enhancement of mean entrainment velocity,
![]() $w_{e}-w_{e,c}$
, can be split into two contributions by factorizing
$w_{e}-w_{e,c}$
, can be split into two contributions by factorizing
![]() $z_{i,f}-(z_{i,f})_{c}$
as the product of
$z_{i,f}-(z_{i,f})_{c}$
as the product of
![]() $[z_{i,f}-(z_{i,f})_{c}]/z_{enc}$
and
$[z_{i,f}-(z_{i,f})_{c}]/z_{enc}$
and
![]() $z_{enc}$
, which yields
$z_{enc}$
, which yields
We have introduced the mean encroachment velocity
![]() $w_{enc}\equiv \text{d}_{t}z_{enc}$
, which can be written as
$w_{enc}\equiv \text{d}_{t}z_{enc}$
, which can be written as
![]() $w_{enc}\simeq N_{0}L_{0}^{2}/z_{enc}$
by using (2.10). The first contribution is positive and represents a quasi-steady contribution to the shear enhancement of the entrainment velocity due to penetrative convection of a CBL that is deeper than in shear-free conditions. The second contribution is negative and represents the unsteady contribution due to the reduction of shear effects in time as the CBL grows and approaches the shear-free limit. As inferred from table 1, the ratio
$w_{enc}\simeq N_{0}L_{0}^{2}/z_{enc}$
by using (2.10). The first contribution is positive and represents a quasi-steady contribution to the shear enhancement of the entrainment velocity due to penetrative convection of a CBL that is deeper than in shear-free conditions. The second contribution is negative and represents the unsteady contribution due to the reduction of shear effects in time as the CBL grows and approaches the shear-free limit. As inferred from table 1, the ratio
![]() $[z_{i,f}-(z_{i,f})_{c}]/z_{enc}$
for
$[z_{i,f}-(z_{i,f})_{c}]/z_{enc}$
for
![]() $Fr_{0}=25$
changes less than 40 % when
$Fr_{0}=25$
changes less than 40 % when
![]() $z_{enc}$
changes by an order of one. Since
$z_{enc}$
changes by an order of one. Since
![]() $[z_{i,f}-(z_{i,f})_{c}]/z_{enc}$
is of the order of
$[z_{i,f}-(z_{i,f})_{c}]/z_{enc}$
is of the order of
![]() $0.15$
, neglecting the second term implies an error of
$0.15$
, neglecting the second term implies an error of
![]() $\simeq 5\,\%$
in the mean entrainment velocity
$\simeq 5\,\%$
in the mean entrainment velocity
![]() $w_{e}$
, which suggests neglecting this unsteady contribution as a first approximation. With this approximation, the mean entrainment velocity can be written as
$w_{e}$
, which suggests neglecting this unsteady contribution as a first approximation. With this approximation, the mean entrainment velocity can be written as
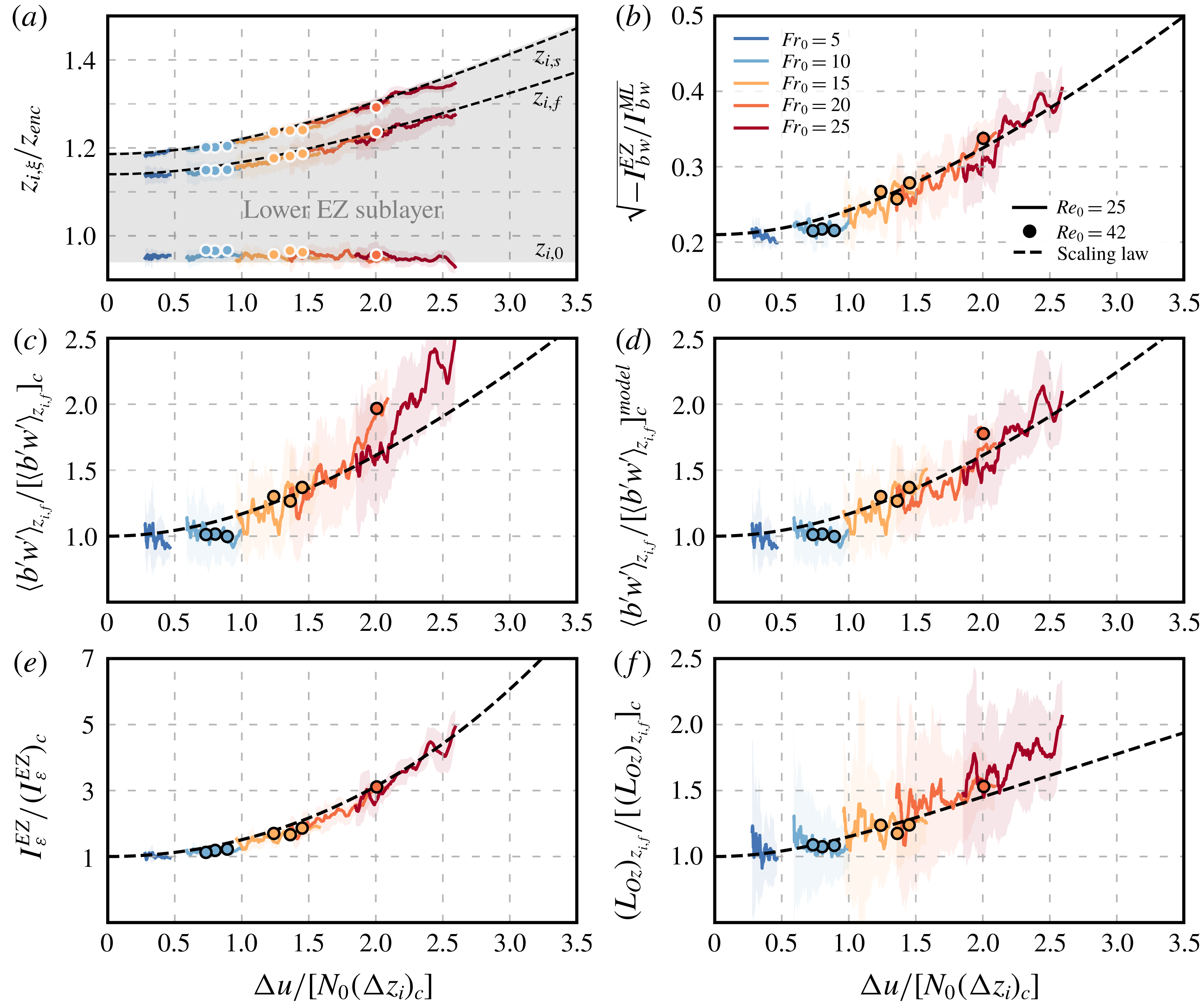
Figure 15. Verification with DNS data (coloured lines) of the scaling laws for the entrainment-zone properties derived in § 5 (dashed lines): (a) reference heights, (b,c,d) buoyancy-flux properties, (e) viscous dissipation rate, and (f) Ozmidov length.
Substituting (5.8) into (5.6), using the relationship
![]() $w_{enc}\simeq N_{0}L_{0}^{2}/z_{enc}$
, and using (4.12a
) to express
$w_{enc}\simeq N_{0}L_{0}^{2}/z_{enc}$
, and using (4.12a
) to express
![]() $z_{i,f}$
in terms of
$z_{i,f}$
in terms of
![]() $z_{enc}$
and
$z_{enc}$
and
![]() $\unicode[STIX]{x0394}z_{i}$
, we can derive a cubic equation for
$\unicode[STIX]{x0394}z_{i}$
, we can derive a cubic equation for
![]() $\unicode[STIX]{x0394}z_{i}/z_{enc}$
. This cubic equation, however, can be easily approximated by a simpler quadratic equation. To this end, we rewrite (5.6) as
$\unicode[STIX]{x0394}z_{i}/z_{enc}$
. This cubic equation, however, can be easily approximated by a simpler quadratic equation. To this end, we rewrite (5.6) as
Approximating
![]() $w_{e}$
using (5.8), we can show that the ratio of the second to the first term satisfies
$w_{e}$
using (5.8), we can show that the ratio of the second to the first term satisfies
where the upper bound is obtained by using the inequality
![]() $(\unicode[STIX]{x0394}z_{i})_{c}<\unicode[STIX]{x0394}z_{i}$
and the definition
$(\unicode[STIX]{x0394}z_{i})_{c}<\unicode[STIX]{x0394}z_{i}$
and the definition
![]() $(\unicode[STIX]{x0394}z_{i})_{c}\equiv 0.25z_{enc}$
. This estimate is confirmed by the data, which show that the ratio of the second to the first term in (5.9) is less than 0.04 (not shown). Hence, we can neglect the second term in (5.9), which leads to
$(\unicode[STIX]{x0394}z_{i})_{c}\equiv 0.25z_{enc}$
. This estimate is confirmed by the data, which show that the ratio of the second to the first term in (5.9) is less than 0.04 (not shown). Hence, we can neglect the second term in (5.9), which leads to
as an explicit expression for the EZ scale in terms of the controlling parameters and the velocity increment across the entrainment zone. The proposed scaling law for
![]() $\unicode[STIX]{x0394}z_{i}$
is supported in figure 15(a), where the reference heights
$\unicode[STIX]{x0394}z_{i}$
is supported in figure 15(a), where the reference heights
![]() $z_{i,f}$
and
$z_{i,f}$
and
![]() $z_{i,s}$
calculated by (4.12a
) and (4.12b
) using
$z_{i,s}$
calculated by (4.12a
) and (4.12b
) using
![]() $\unicode[STIX]{x0394}z_{i}$
obtained from (5.11) agree with the DNS data. The small deviation between the scaling laws and the DNS data for
$\unicode[STIX]{x0394}z_{i}$
obtained from (5.11) agree with the DNS data. The small deviation between the scaling laws and the DNS data for
![]() $Fr_{0}=10$
and
$Fr_{0}=10$
and
![]() $15$
in figure 15(a) is due to the neglect of the turbulent flux of TKE in (5.1), but, as already indicated before, the shear effects in those cases are still relatively small. Comparing the data from cases
$15$
in figure 15(a) is due to the neglect of the turbulent flux of TKE in (5.1), but, as already indicated before, the shear effects in those cases are still relatively small. Comparing the data from cases
![]() $Re_{0}=25$
and
$Re_{0}=25$
and
![]() $Re_{0}=42$
shows that the Reynolds-number dependence of these scaling laws is small, less than the achieved statistical convergence. Substituting the expression for
$Re_{0}=42$
shows that the Reynolds-number dependence of these scaling laws is small, less than the achieved statistical convergence. Substituting the expression for
![]() $z_{i,f}$
, (4.12a
), into (5.8), we obtain
$z_{i,f}$
, (4.12a
), into (5.8), we obtain
as an explicit expression for the mean entrainment velocity in the barotropic CBLs considered in this study. The convective limits are
![]() $w_{e,c}\simeq 1.14N_{0}L_{0}^{2}/z_{enc}$
, from (5.5) and (4.12a
), and
$w_{e,c}\simeq 1.14N_{0}L_{0}^{2}/z_{enc}$
, from (5.5) and (4.12a
), and
![]() $(\unicode[STIX]{x0394}z_{i})_{c}\equiv 0.25z_{enc}$
, from (4.9).
$(\unicode[STIX]{x0394}z_{i})_{c}\equiv 0.25z_{enc}$
, from (4.9).
5.2 Scaling law for buoyancy-flux properties
Besides
![]() $z_{i,f}$
and
$z_{i,f}$
and
![]() $\unicode[STIX]{x0394}z_{i}$
, other properties that are relevant to characterize the entrainment zone are the ratio between the minimum turbulent buoyancy flux and the surface buoyancy flux,
$\unicode[STIX]{x0394}z_{i}$
, other properties that are relevant to characterize the entrainment zone are the ratio between the minimum turbulent buoyancy flux and the surface buoyancy flux,
![]() $-\langle b^{\prime }w^{\prime }\rangle _{z_{i,f}}/B_{0}$
, referred to as the entrainment-flux ratio (Pino et al.
Reference Pino, Vilà-Guerau De Arellano and Duynkerke2003; Conzemius & Fedorovich Reference Conzemius and Fedorovich2006a
; Pino, Vilà-Guerau De Arellano & Kim Reference Pino, Vilà-Guerau De Arellano and Kim2006), and the square root of the ratio between the negative and positive areas of the turbulent buoyancy flux,
$-\langle b^{\prime }w^{\prime }\rangle _{z_{i,f}}/B_{0}$
, referred to as the entrainment-flux ratio (Pino et al.
Reference Pino, Vilà-Guerau De Arellano and Duynkerke2003; Conzemius & Fedorovich Reference Conzemius and Fedorovich2006a
; Pino, Vilà-Guerau De Arellano & Kim Reference Pino, Vilà-Guerau De Arellano and Kim2006), and the square root of the ratio between the negative and positive areas of the turbulent buoyancy flux,
![]() $(-I_{bw}^{EZ}/I_{bw}^{ML})^{1/2}$
, where the superscript
$(-I_{bw}^{EZ}/I_{bw}^{ML})^{1/2}$
, where the superscript
![]() $ML$
stands for the mixed layer and indicates that the corresponding integral is calculated in the interval
$ML$
stands for the mixed layer and indicates that the corresponding integral is calculated in the interval
![]() $0<z<z_{i,0}$
(Conzemius & Fedorovich Reference Conzemius and Fedorovich2006a
).
$0<z<z_{i,0}$
(Conzemius & Fedorovich Reference Conzemius and Fedorovich2006a
).
An estimate for
![]() $(-I_{bw}^{EZ}/I_{bw}^{ML})^{1/2}$
can be obtained as follows. From the relationship
$(-I_{bw}^{EZ}/I_{bw}^{ML})^{1/2}$
can be obtained as follows. From the relationship
![]() $-I_{bw}^{EZ}\sim w_{e}\unicode[STIX]{x0394}b\unicode[STIX]{x0394}z_{i}=w_{e}N_{0}^{2}\unicode[STIX]{x0394}z_{i}^{2}$
used before, estimating the corresponding coefficient of proportionality as 0.3 according to figure 14(
$-I_{bw}^{EZ}\sim w_{e}\unicode[STIX]{x0394}b\unicode[STIX]{x0394}z_{i}=w_{e}N_{0}^{2}\unicode[STIX]{x0394}z_{i}^{2}$
used before, estimating the corresponding coefficient of proportionality as 0.3 according to figure 14(
![]() $c$
), and using the approximation
$c$
), and using the approximation
![]() $I_{bw}^{ML}\simeq 0.5B_{0}z_{enc}$
based on the linear variation of the turbulent buoyancy flux between the surface and
$I_{bw}^{ML}\simeq 0.5B_{0}z_{enc}$
based on the linear variation of the turbulent buoyancy flux between the surface and
![]() $z_{i,0}$
(see figure 7
a), the area ratio can be expressed as
$z_{i,0}$
(see figure 7
a), the area ratio can be expressed as
where we have used (5.12) to express the result in terms of
![]() $\unicode[STIX]{x0394}z_{i}/(\unicode[STIX]{x0394}z_{i})_{c}$
. This scaling law is supported by the DNS data in figure 15(b). Consistent with previous work, we obtain a value
$\unicode[STIX]{x0394}z_{i}/(\unicode[STIX]{x0394}z_{i})_{c}$
. This scaling law is supported by the DNS data in figure 15(b). Consistent with previous work, we obtain a value
![]() $\simeq 0.2$
in the shear-free limit (Conzemius & Fedorovich Reference Conzemius and Fedorovich2006a
).
$\simeq 0.2$
in the shear-free limit (Conzemius & Fedorovich Reference Conzemius and Fedorovich2006a
).
An estimate for
![]() $-\langle b^{\prime }w^{\prime }\rangle _{z_{i,f}}/B_{0}$
can be obtained in a similar way. From the scaling law
$-\langle b^{\prime }w^{\prime }\rangle _{z_{i,f}}/B_{0}$
can be obtained in a similar way. From the scaling law
![]() $-\langle b^{\prime }w^{\prime }\rangle _{z_{i,f}}\sim w_{e}\unicode[STIX]{x0394}b=w_{e}N_{0}^{2}\unicode[STIX]{x0394}z_{i}$
employed before and using (5.12), we obtain
$-\langle b^{\prime }w^{\prime }\rangle _{z_{i,f}}\sim w_{e}\unicode[STIX]{x0394}b=w_{e}N_{0}^{2}\unicode[STIX]{x0394}z_{i}$
employed before and using (5.12), we obtain
This scaling law is supported by the DNS data in figure 15(c). The deviation of
![]() $\simeq 20\,\%$
for strong wind conditions is a Reynolds-number effect. For the cases with
$\simeq 20\,\%$
for strong wind conditions is a Reynolds-number effect. For the cases with
![]() $Re_{0}=25$
, the turbulent Reynolds number at
$Re_{0}=25$
, the turbulent Reynolds number at
![]() $z=z_{i,f}$
,
$z=z_{i,f}$
,
![]() $(Re_{t})_{z_{i,f}}$
, is approximately four times larger for cases
$(Re_{t})_{z_{i,f}}$
, is approximately four times larger for cases
![]() $Fr_{0}=20$
and
$Fr_{0}=20$
and
![]() $Fr_{0}=25$
than for case
$Fr_{0}=25$
than for case
![]() $Fr_{0}=0$
(1600 compared to 400, as seen in table 1). A similar variation in
$Fr_{0}=0$
(1600 compared to 400, as seen in table 1). A similar variation in
![]() $Re_{t}$
is observed between cases
$Re_{t}$
is observed between cases
![]() $Re_{0}=25$
and
$Re_{0}=25$
and
![]() $Re_{0}=117$
in shear-free conditions, and the entrainment-flux ratio in shear-free conditions, which is used to normalize the entrainment-flux ratio in sheared conditions, varies approximately 30 % over this interval of Reynolds number (see figure 16
a). Normalizing the minimum buoyancy flux for cases
$Re_{0}=117$
in shear-free conditions, and the entrainment-flux ratio in shear-free conditions, which is used to normalize the entrainment-flux ratio in sheared conditions, varies approximately 30 % over this interval of Reynolds number (see figure 16
a). Normalizing the minimum buoyancy flux for cases
![]() $Fr_{0}=20$
and
$Fr_{0}=20$
and
![]() $Fr_{0}=25$
with the approximation
$Fr_{0}=25$
with the approximation
which is derived in Garcia & Mellado (Reference Garcia and Mellado2014) from data at
![]() $Re_{t}\simeq 1600$
and hence turbulent Reynolds numbers that are comparable to the ones here in the strong shear conditions, (5.14) represents better the DNS data, as shown in figure 15(d).
$Re_{t}\simeq 1600$
and hence turbulent Reynolds numbers that are comparable to the ones here in the strong shear conditions, (5.14) represents better the DNS data, as shown in figure 15(d).
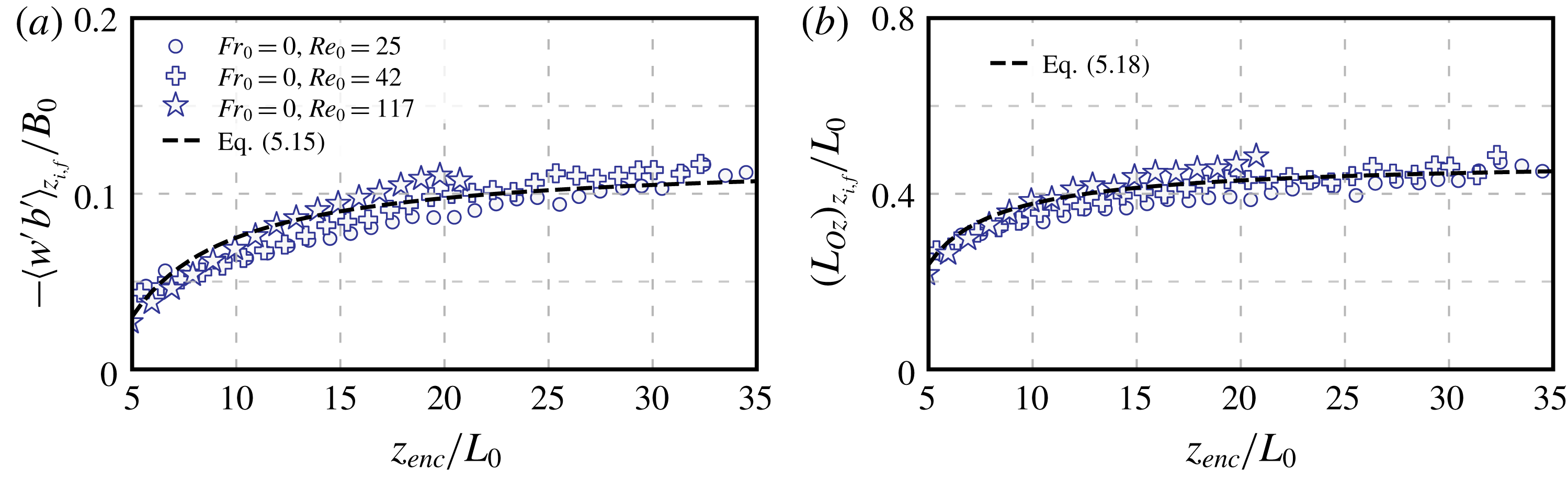
Figure 16. Temporal evolution of (a) the entrainment-flux ratio,
![]() $\langle b^{\prime }w^{\prime }\rangle _{z_{i,f}}/B_{0}$
, and (b) the normalized Ozmidov length particularized at the height of the minimum buoyancy flux,
$\langle b^{\prime }w^{\prime }\rangle _{z_{i,f}}/B_{0}$
, and (b) the normalized Ozmidov length particularized at the height of the minimum buoyancy flux,
![]() $(L_{Oz})_{z_{i,f}}/L_{0}$
, in the shear-free CBL. Symbols indicate the average within an interval
$(L_{Oz})_{z_{i,f}}/L_{0}$
, in the shear-free CBL. Symbols indicate the average within an interval
![]() $\unicode[STIX]{x0394}z_{enc}/L_{0}=2$
.
$\unicode[STIX]{x0394}z_{enc}/L_{0}=2$
.
The scaling laws (5.13) and (5.14) do not feature a reduction of entrainment flux for weak shear conditions. The slight decrease observed in figure 15(c,d) for the case
![]() $Fr_{0}=5$
near
$Fr_{0}=5$
near
![]() $\unicode[STIX]{x0394}u/[N_{0}(\unicode[STIX]{x0394}z_{i})_{c}]=0.5$
is smaller than the statistical convergence of our data, as indicated in figure 15 by the shaded regions. Besides, those values correspond to an early stage of the quasi-steady regime, which is not observed in the case
$\unicode[STIX]{x0394}u/[N_{0}(\unicode[STIX]{x0394}z_{i})_{c}]=0.5$
is smaller than the statistical convergence of our data, as indicated in figure 15 by the shaded regions. Besides, those values correspond to an early stage of the quasi-steady regime, which is not observed in the case
![]() $Fr_{0}=10$
near
$Fr_{0}=10$
near
![]() $\unicode[STIX]{x0394}u/[N_{0}(\unicode[STIX]{x0394}z_{i})_{c}]=0.5$
, where the CBL is further into the quasi-steady regime and the local turbulent Reynolds number is six times larger. We recall that, for weak shear conditions, the analysis of the TKE budget equation presented in § 5.2 indicates that the shear production of TKE is mostly used to modify the transport of TKE in and out of the entrainment zone without significantly affecting the buoyancy flux and the dissipation rate, at least, to the accuracy achieved by our simulations.
$\unicode[STIX]{x0394}u/[N_{0}(\unicode[STIX]{x0394}z_{i})_{c}]=0.5$
, where the CBL is further into the quasi-steady regime and the local turbulent Reynolds number is six times larger. We recall that, for weak shear conditions, the analysis of the TKE budget equation presented in § 5.2 indicates that the shear production of TKE is mostly used to modify the transport of TKE in and out of the entrainment zone without significantly affecting the buoyancy flux and the dissipation rate, at least, to the accuracy achieved by our simulations.
5.3 Scaling law for the Ozmidov length
To reconstruct the complete entrainment-zone structure using (4.12) one needs a scaling law for the Ozmidov length
![]() $(L_{Oz})_{z_{i,f}}$
in addition to the scaling law (5.11) for the EZ scale
$(L_{Oz})_{z_{i,f}}$
in addition to the scaling law (5.11) for the EZ scale
![]() $\unicode[STIX]{x0394}z_{i}$
. From the definition of the Ozmidov length (2.5), this implies obtaining a scaling law for the viscous dissipation rate at the height of minimum buoyancy flux. Such a scaling law can be obtained from the relationship (5.3), which states that changes in the dissipation rate relative to the shear-free limit are well scaled by the changes in the buoyancy flux, the constant of proportionality being
$\unicode[STIX]{x0394}z_{i}$
. From the definition of the Ozmidov length (2.5), this implies obtaining a scaling law for the viscous dissipation rate at the height of minimum buoyancy flux. Such a scaling law can be obtained from the relationship (5.3), which states that changes in the dissipation rate relative to the shear-free limit are well scaled by the changes in the buoyancy flux, the constant of proportionality being
![]() $\simeq 0.3$
, as observed in figure 14(a). Hence, we can write
$\simeq 0.3$
, as observed in figure 14(a). Hence, we can write
where the proportionality constant is
![]() $c_{2}\equiv -(I_{bw}^{EZ})_{c}/[0.3(I_{\unicode[STIX]{x1D700}}^{EZ})_{c}]$
and we have used the approximation
$c_{2}\equiv -(I_{bw}^{EZ})_{c}/[0.3(I_{\unicode[STIX]{x1D700}}^{EZ})_{c}]$
and we have used the approximation
![]() $-I_{bw}^{EZ}\simeq 0.3w_{e}N_{0}^{2}\unicode[STIX]{x0394}z_{i}^{2}$
employed before to derive (5.13). The ratio of mean entrainment velocities in the equation above is provided by (5.12). To evaluate the proportionality constant
$-I_{bw}^{EZ}\simeq 0.3w_{e}N_{0}^{2}\unicode[STIX]{x0394}z_{i}^{2}$
employed before to derive (5.13). The ratio of mean entrainment velocities in the equation above is provided by (5.12). To evaluate the proportionality constant
![]() $c_{2}$
, we know that
$c_{2}$
, we know that
![]() $-(I_{bw}^{EZ})_{c}\simeq 0.022B_{0}z_{enc}$
by substituting
$-(I_{bw}^{EZ})_{c}\simeq 0.022B_{0}z_{enc}$
by substituting
![]() $\unicode[STIX]{x0394}z_{i}=(\unicode[STIX]{x0394}z_{i})_{c}$
into (5.13), and we know that
$\unicode[STIX]{x0394}z_{i}=(\unicode[STIX]{x0394}z_{i})_{c}$
into (5.13), and we know that
![]() $(I_{\unicode[STIX]{x1D700}}^{EZ})_{c}\simeq (I_{T}^{EZ}+I_{bw}^{EZ})_{c}$
from the TKE budget equation for shear-free conditions, which yields
$(I_{\unicode[STIX]{x1D700}}^{EZ})_{c}\simeq (I_{T}^{EZ}+I_{bw}^{EZ})_{c}$
from the TKE budget equation for shear-free conditions, which yields
![]() $(I_{\unicode[STIX]{x1D700}}^{EZ})_{c}\simeq 0.048B_{0}z_{enc}$
when we use the estimate
$(I_{\unicode[STIX]{x1D700}}^{EZ})_{c}\simeq 0.048B_{0}z_{enc}$
when we use the estimate
![]() $(I_{T}^{EZ})_{c}\simeq 0.07B_{0}z_{enc}$
from figure 13(
$(I_{T}^{EZ})_{c}\simeq 0.07B_{0}z_{enc}$
from figure 13(
![]() $c$
). The value that we obtain is
$c$
). The value that we obtain is
![]() $c_{2}\simeq 1.53$
and the resulting scaling law (5.16) is validated with the DNS data in figure 15(e).
$c_{2}\simeq 1.53$
and the resulting scaling law (5.16) is validated with the DNS data in figure 15(e).
To find the scaling law for the Ozmidov length at
![]() $z_{i,f}$
, we define a characteristic scale for the dissipation rate in the entrainment zone as
$z_{i,f}$
, we define a characteristic scale for the dissipation rate in the entrainment zone as
![]() $I_{\unicode[STIX]{x1D700}}^{EZ}/\unicode[STIX]{x0394}z_{i}$
. From definition (2.5), we obtain the following ratio of the Ozmidov length between sheared conditions and shear-free conditions:
$I_{\unicode[STIX]{x1D700}}^{EZ}/\unicode[STIX]{x0394}z_{i}$
. From definition (2.5), we obtain the following ratio of the Ozmidov length between sheared conditions and shear-free conditions:
where the ratio of mean entrainment velocities is given by (5.12) as a function
![]() $\unicode[STIX]{x0394}z_{i}/(\unicode[STIX]{x0394}z_{i})_{c}$
. This scaling law is supported in figure 15(f). The deviation of
$\unicode[STIX]{x0394}z_{i}/(\unicode[STIX]{x0394}z_{i})_{c}$
. This scaling law is supported in figure 15(f). The deviation of
![]() $\simeq 20\,\%$
for strong wind conditions is a Reynolds-number effect, which, as explained in § 5.2, arises because the Ozmidov length in sheared conditions is normalized by the shear-free value, and the latter varies approximately 15 % within the interval of turbulent Reynolds numbers in the entrainment zone spanned between cases
$\simeq 20\,\%$
for strong wind conditions is a Reynolds-number effect, which, as explained in § 5.2, arises because the Ozmidov length in sheared conditions is normalized by the shear-free value, and the latter varies approximately 15 % within the interval of turbulent Reynolds numbers in the entrainment zone spanned between cases
![]() $Fr_{0}=0$
and
$Fr_{0}=0$
and
![]() $Fr_{0}=25$
(cf. figure 16
b). As a first approximation, one can consider
$Fr_{0}=25$
(cf. figure 16
b). As a first approximation, one can consider
which is obtained from definition (2.5), from (5.15) and from
![]() $(\unicode[STIX]{x2202}_{z}\langle b\rangle )_{z_{i,f}}\simeq 0.9N_{0}^{2}$
(see figure 11
b) and the observation that
$(\unicode[STIX]{x2202}_{z}\langle b\rangle )_{z_{i,f}}\simeq 0.9N_{0}^{2}$
(see figure 11
b) and the observation that
![]() $(-\unicode[STIX]{x1D700}/\langle b^{\prime }w^{\prime }\rangle )_{z_{i,f}}\simeq 1.6$
according to figure 7(a). Normalizing the Ozmidov scale in sheared CBLs with the shear-free limit provided by (5.18) represents better the DNS data (not shown).
$(-\unicode[STIX]{x1D700}/\langle b^{\prime }w^{\prime }\rangle )_{z_{i,f}}\simeq 1.6$
according to figure 7(a). Normalizing the Ozmidov scale in sheared CBLs with the shear-free limit provided by (5.18) represents better the DNS data (not shown).
6 Discussion
The scaling laws (4.12) for the reference heights, (5.11) for the EZ scale, (5.17) for the Ozmidov length and (5.14) for the entrainment-flux ratio help characterize the two-layer structure of the entrainment zone in the equilibrium (quasi-steady) entrainment regime of a barotropic CBL penetrating into a linearly stratified atmosphere. We are still lacking a relationship between the velocity increment
![]() $\unicode[STIX]{x0394}u$
, the control parameter
$\unicode[STIX]{x0394}u$
, the control parameter
![]() $Fr_{0}$
and the independent variable
$Fr_{0}$
and the independent variable
![]() $z_{enc}/L_{0}$
. This relationship could be obtained from the integral analysis of the momentum equation between
$z_{enc}/L_{0}$
. This relationship could be obtained from the integral analysis of the momentum equation between
![]() $z=0$
and
$z=0$
and
![]() $z=z_{i,f}$
, but such an analysis requires the study of the friction velocity and its dependence on surface properties, e.g. on the Reynolds number for an aerodynamically smooth wall or on the roughness properties for an aerodynamically rough wall, and such a study deserves its own paper. Nonetheless, the proposed characterization of entrainment-zone properties in terms of
$z=z_{i,f}$
, but such an analysis requires the study of the friction velocity and its dependence on surface properties, e.g. on the Reynolds number for an aerodynamically smooth wall or on the roughness properties for an aerodynamically rough wall, and such a study deserves its own paper. Nonetheless, the proposed characterization of entrainment-zone properties in terms of
![]() $\unicode[STIX]{x0394}u/(N_{0}L_{0})$
and
$\unicode[STIX]{x0394}u/(N_{0}L_{0})$
and
![]() $z_{enc}/L_{0}$
should remain approximately valid for different surface properties because, as reviewed in the introduction and shown in § 3, the shear near the surface affects entrainment mainly indirectly through the change of
$z_{enc}/L_{0}$
should remain approximately valid for different surface properties because, as reviewed in the introduction and shown in § 3, the shear near the surface affects entrainment mainly indirectly through the change of
![]() $\unicode[STIX]{x0394}u$
. Besides, scaling laws in terms of
$\unicode[STIX]{x0394}u$
. Besides, scaling laws in terms of
![]() $\unicode[STIX]{x0394}u$
are convenient because
$\unicode[STIX]{x0394}u$
are convenient because
![]() $\unicode[STIX]{x0394}u$
might be more easily measured and simulated than local properties in the entrainment zone, such as
$\unicode[STIX]{x0394}u$
might be more easily measured and simulated than local properties in the entrainment zone, such as
![]() $\unicode[STIX]{x0394}z_{i}$
. The reason is that the mean velocity profile is approximately height-invariant inside the mixed layer and inside the free atmosphere, and hence
$\unicode[STIX]{x0394}z_{i}$
. The reason is that the mean velocity profile is approximately height-invariant inside the mixed layer and inside the free atmosphere, and hence
![]() $\unicode[STIX]{x0394}u$
is insensitive to the exact location where those two velocity values are calculated.
$\unicode[STIX]{x0394}u$
is insensitive to the exact location where those two velocity values are calculated.
The independent variable
![]() $\unicode[STIX]{x0394}u/[N_{0}(\unicode[STIX]{x0394}z_{i})_{c}]$
can be interpreted in various ways. From (4.10), the definition of
$\unicode[STIX]{x0394}u/[N_{0}(\unicode[STIX]{x0394}z_{i})_{c}]$
can be interpreted in various ways. From (4.10), the definition of
![]() $(\unicode[STIX]{x0394}z_{i})_{s}$
, we can write
$(\unicode[STIX]{x0394}z_{i})_{s}$
, we can write
![]() $\unicode[STIX]{x0394}u/[N_{0}(\unicode[STIX]{x0394}z_{i})_{c}]=\sqrt{3}(\unicode[STIX]{x0394}z_{i})_{s}/(\unicode[STIX]{x0394}z_{i})_{c}$
and use
$\unicode[STIX]{x0394}u/[N_{0}(\unicode[STIX]{x0394}z_{i})_{c}]=\sqrt{3}(\unicode[STIX]{x0394}z_{i})_{s}/(\unicode[STIX]{x0394}z_{i})_{c}$
and use
![]() $(\unicode[STIX]{x0394}z_{i})_{s}/(\unicode[STIX]{x0394}z_{i})_{c}$
as the independent variable, which can be interpreted as the ratio between the shear limit and the convective limit of the EZ scale. Under strongly unstable conditions (weak wind),
$(\unicode[STIX]{x0394}z_{i})_{s}/(\unicode[STIX]{x0394}z_{i})_{c}$
as the independent variable, which can be interpreted as the ratio between the shear limit and the convective limit of the EZ scale. Under strongly unstable conditions (weak wind),
![]() $(\unicode[STIX]{x0394}z_{i})_{s}$
is smaller than
$(\unicode[STIX]{x0394}z_{i})_{s}$
is smaller than
![]() $(\unicode[STIX]{x0394}z_{i})_{c}$
, and the latter characterizes the lower EZ sublayer. For weakly unstable conditions (strong wind),
$(\unicode[STIX]{x0394}z_{i})_{c}$
, and the latter characterizes the lower EZ sublayer. For weakly unstable conditions (strong wind),
![]() $(\unicode[STIX]{x0394}z_{i})_{s}$
is comparable to
$(\unicode[STIX]{x0394}z_{i})_{s}$
is comparable to
![]() $(\unicode[STIX]{x0394}z_{i})_{c}$
and characterizes the lower EZ sublayer.
$(\unicode[STIX]{x0394}z_{i})_{c}$
and characterizes the lower EZ sublayer.
A second interpretation of
![]() $\unicode[STIX]{x0394}u/[N_{0}(\unicode[STIX]{x0394}z_{i})_{c}]$
can be obtained by using (4.9), the definition of
$\unicode[STIX]{x0394}u/[N_{0}(\unicode[STIX]{x0394}z_{i})_{c}]$
can be obtained by using (4.9), the definition of
![]() $(\unicode[STIX]{x0394}z_{i})_{c}$
, to write
$(\unicode[STIX]{x0394}z_{i})_{c}$
, to write
![]() $\unicode[STIX]{x0394}u/[N_{0}(\unicode[STIX]{x0394}z_{i})_{c}]=4\unicode[STIX]{x0394}u/(N_{0}z_{enc})$
. We can then use
$\unicode[STIX]{x0394}u/[N_{0}(\unicode[STIX]{x0394}z_{i})_{c}]=4\unicode[STIX]{x0394}u/(N_{0}z_{enc})$
. We can then use
as the independent variable, which can be interpreted as a bulk Richardson number that compares the energy necessary for a fluid particle to penetrate a distance
![]() $z_{enc}$
into the free atmosphere, and the kinetic energy associated with the velocity difference across the entrainment zone.
$z_{enc}$
into the free atmosphere, and the kinetic energy associated with the velocity difference across the entrainment zone.
This definition of a bulk Richardson number differs from the definition
![]() $\widetilde{Ri}_{b}\equiv \widetilde{\unicode[STIX]{x0394}b}z_{i,f}/\unicode[STIX]{x0394}u^{2}$
often used in previous analyses (Pino et al.
Reference Pino, Vilà-Guerau De Arellano and Duynkerke2003; Conzemius & Fedorovich Reference Conzemius and Fedorovich2006b
, Reference Conzemius and Fedorovich2007), where
$\widetilde{Ri}_{b}\equiv \widetilde{\unicode[STIX]{x0394}b}z_{i,f}/\unicode[STIX]{x0394}u^{2}$
often used in previous analyses (Pino et al.
Reference Pino, Vilà-Guerau De Arellano and Duynkerke2003; Conzemius & Fedorovich Reference Conzemius and Fedorovich2006b
, Reference Conzemius and Fedorovich2007), where
![]() $\widetilde{\unicode[STIX]{x0394}b}$
represents a measure of the buoyancy increment across the entrainment zone and it is not necessarily equal to the definition
$\widetilde{\unicode[STIX]{x0394}b}$
represents a measure of the buoyancy increment across the entrainment zone and it is not necessarily equal to the definition
![]() $\unicode[STIX]{x0394}b\equiv N_{0}^{2}\unicode[STIX]{x0394}z_{i}$
used here. These previous studies commonly result in an entrainment-flux ratio proportional to
$\unicode[STIX]{x0394}b\equiv N_{0}^{2}\unicode[STIX]{x0394}z_{i}$
used here. These previous studies commonly result in an entrainment-flux ratio proportional to
![]() $(1-a\widetilde{Ri}_{b}^{-1})^{-1}$
, where
$(1-a\widetilde{Ri}_{b}^{-1})^{-1}$
, where
![]() $a\simeq 0.3{-}1.0$
, which can become infinity and hence unphysical for strong wind conditions (Conzemius & Fedorovich Reference Conzemius and Fedorovich2006b
). Differently from these previous studies, we have used the EZ scale
$a\simeq 0.3{-}1.0$
, which can become infinity and hence unphysical for strong wind conditions (Conzemius & Fedorovich Reference Conzemius and Fedorovich2006b
). Differently from these previous studies, we have used the EZ scale
![]() $\unicode[STIX]{x0394}z_{i}$
instead of the CBL depth
$\unicode[STIX]{x0394}z_{i}$
instead of the CBL depth
![]() $z_{i,f}$
to estimate
$z_{i,f}$
to estimate
![]() $I_{bw}^{EZ}$
in the TKE budget analysis presented in § 5. For small values of
$I_{bw}^{EZ}$
in the TKE budget analysis presented in § 5. For small values of
![]() $\unicode[STIX]{x0394}u$
, the two scales
$\unicode[STIX]{x0394}u$
, the two scales
![]() $z_{enc}$
and
$z_{enc}$
and
![]() $z_{i,f}$
are proportional to each other, which implies
$z_{i,f}$
are proportional to each other, which implies
![]() $Ri_{b}\propto \widetilde{Ri}_{b}$
. Besides, for small values of
$Ri_{b}\propto \widetilde{Ri}_{b}$
. Besides, for small values of
![]() $\unicode[STIX]{x0394}u$
, the Taylor expansion of (5.14) yields
$\unicode[STIX]{x0394}u$
, the Taylor expansion of (5.14) yields
![]() $\langle b^{\prime }w^{\prime }\rangle _{z_{i,f}}/[\langle b^{\prime }w^{\prime }\rangle _{z_{i,f}}]_{c}\simeq 1+2.8Ri_{b}^{-1}$
, where the linear dependence on
$\langle b^{\prime }w^{\prime }\rangle _{z_{i,f}}/[\langle b^{\prime }w^{\prime }\rangle _{z_{i,f}}]_{c}\simeq 1+2.8Ri_{b}^{-1}$
, where the linear dependence on
![]() $Ri_{b}^{-1}$
agrees with that obtained from the expansion
$Ri_{b}^{-1}$
agrees with that obtained from the expansion
![]() $(1-a\widetilde{Ri}_{b}^{-1})^{-1}\simeq 1+a\widetilde{Ri}_{b}^{-1}$
for large values of
$(1-a\widetilde{Ri}_{b}^{-1})^{-1}\simeq 1+a\widetilde{Ri}_{b}^{-1}$
for large values of
![]() $\widetilde{Ri}_{b}$
. However, for larger values of
$\widetilde{Ri}_{b}$
. However, for larger values of
![]() $\unicode[STIX]{x0394}u$
, the length scales
$\unicode[STIX]{x0394}u$
, the length scales
![]() $z_{enc}$
and
$z_{enc}$
and
![]() $z_{i,f}$
differ,
$z_{i,f}$
differ,
![]() $Ri_{b}$
and
$Ri_{b}$
and
![]() $\widetilde{Ri}_{b}$
are not proportional to each other, and the scaling laws derived here remain finite for strong wind conditions.
$\widetilde{Ri}_{b}$
are not proportional to each other, and the scaling laws derived here remain finite for strong wind conditions.
We can use the scaling laws derived above to construct a partition of the parameter space depending on the relevance of shear in the entrainment zone. We choose to measure this relevance by the ratio between the shear-production rate and the turbulent-transport rate, since this variable is often used in the literature to discuss shear effects. We define the convective-dominated regime when
![]() $[P/(-\unicode[STIX]{x2202}_{z}T)]_{z_{i,f}}\lesssim 0.5$
and the shear-dominated regime when
$[P/(-\unicode[STIX]{x2202}_{z}T)]_{z_{i,f}}\lesssim 0.5$
and the shear-dominated regime when
![]() $[P/(-\unicode[STIX]{x2202}_{z}T)]_{z_{i,f}}\gtrsim 2$
. These limits are indicated in figure 8(a), the grey area in between corresponding to conditions in which both shear and convection are important for entrainment-zone properties. These limits are also indicated in terms of the flux Richardson number in figure 8(b). As observed previously in the literature (Conzemius & Fedorovich Reference Conzemius and Fedorovich2006a
; Pino & Vilà-Guerau De Arellano Reference Pino and Vilà-Guerau De Arellano2008), we find that wind-shear effects appear at flux Richardson numbers of order one, which is significantly larger than the asymptotic value
$[P/(-\unicode[STIX]{x2202}_{z}T)]_{z_{i,f}}\gtrsim 2$
. These limits are indicated in figure 8(a), the grey area in between corresponding to conditions in which both shear and convection are important for entrainment-zone properties. These limits are also indicated in terms of the flux Richardson number in figure 8(b). As observed previously in the literature (Conzemius & Fedorovich Reference Conzemius and Fedorovich2006a
; Pino & Vilà-Guerau De Arellano Reference Pino and Vilà-Guerau De Arellano2008), we find that wind-shear effects appear at flux Richardson numbers of order one, which is significantly larger than the asymptotic value
![]() $\simeq 0.25{-}0.3$
characteristic of marginally stable stratified shear layers. As explained before with the help of (5.6), the value
$\simeq 0.25{-}0.3$
characteristic of marginally stable stratified shear layers. As explained before with the help of (5.6), the value
![]() $\simeq 0.25{-}0.3$
is recovered when we subtract the buoyancy flux in shear-free conditions from the buoyancy flux in sheared conditions.
$\simeq 0.25{-}0.3$
is recovered when we subtract the buoyancy flux in shear-free conditions from the buoyancy flux in sheared conditions.
Plotting
![]() $[P/(-\unicode[STIX]{x2202}_{z}T)]_{z_{i,f}}$
as a function of
$[P/(-\unicode[STIX]{x2202}_{z}T)]_{z_{i,f}}$
as a function of
![]() $\unicode[STIX]{x0394}u/[N_{0}(\unicode[STIX]{x0394}z_{i})_{c}]$
(not shown), we can express the thresholds that define the convective-dominated regime and the shear-dominated regime in terms of
$\unicode[STIX]{x0394}u/[N_{0}(\unicode[STIX]{x0394}z_{i})_{c}]$
(not shown), we can express the thresholds that define the convective-dominated regime and the shear-dominated regime in terms of
![]() $\unicode[STIX]{x0394}u/[N_{0}(\unicode[STIX]{x0394}z_{i})_{c}]$
. We find that the upper threshold for the convection-dominated regime corresponds to
$\unicode[STIX]{x0394}u/[N_{0}(\unicode[STIX]{x0394}z_{i})_{c}]$
. We find that the upper threshold for the convection-dominated regime corresponds to
and the lower threshold for the shear-dominated regime corresponds to
The corresponding thresholds in terms of other independent variables are summarized in table 3. The critical value of
![]() $\unicode[STIX]{x0394}u/[N_{0}(\unicode[STIX]{x0394}z_{i})_{c}]=0.6$
corresponds to
$\unicode[STIX]{x0394}u/[N_{0}(\unicode[STIX]{x0394}z_{i})_{c}]=0.6$
corresponds to
![]() $\simeq 5~\text{m}~\text{s}^{-1}$
wind velocity in the free atmosphere for typical midday conditions, which is often considered as a reference value for wind effects to become relevant in unstable conditions (Stull Reference Stull and Stull1988). We note, however, that even such a weak wind could significantly affect the entrainment zone when the buoyancy forcing is weak, e.g. in the early morning or the late evening.
$\simeq 5~\text{m}~\text{s}^{-1}$
wind velocity in the free atmosphere for typical midday conditions, which is often considered as a reference value for wind effects to become relevant in unstable conditions (Stull Reference Stull and Stull1988). We note, however, that even such a weak wind could significantly affect the entrainment zone when the buoyancy forcing is weak, e.g. in the early morning or the late evening.
Table 3. Critical values of various variables defining the boundary of the convection-dominated regime, where shear effects in the entrainment zone are negligible, and the boundary of the shear-dominated regime, where shear effects are of order one or larger.
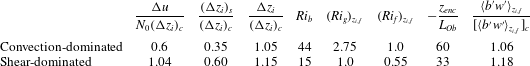
We can represent these various regimes in a parameter space spanned by the normalized velocity jump across the entrainment zone and the normalized convective velocity, as shown in figure 17. Using the definition of the convective velocity scale (2.13), the boundaries between the various regions are
and
Hence, depending on the strength of
![]() $\unicode[STIX]{x0394}u$
and
$\unicode[STIX]{x0394}u$
and
![]() $w_{\ast }$
, the entrainment-zone dynamics in the equilibrium (quasi-steady) entrainment regime of a barotropic CBL penetrating into a linearly stratified atmosphere can be categorized in the following three regimes: the convection-dominated regime for
$w_{\ast }$
, the entrainment-zone dynamics in the equilibrium (quasi-steady) entrainment regime of a barotropic CBL penetrating into a linearly stratified atmosphere can be categorized in the following three regimes: the convection-dominated regime for
![]() $\unicode[STIX]{x0394}u<(\unicode[STIX]{x0394}u)_{conv}$
, a regime in which shear and convective forcing are comparable for
$\unicode[STIX]{x0394}u<(\unicode[STIX]{x0394}u)_{conv}$
, a regime in which shear and convective forcing are comparable for
![]() $(\unicode[STIX]{x0394}u)_{conv}<\unicode[STIX]{x0394}u<(\unicode[STIX]{x0394}u)_{shear}$
, and the shear-dominated regime for
$(\unicode[STIX]{x0394}u)_{conv}<\unicode[STIX]{x0394}u<(\unicode[STIX]{x0394}u)_{shear}$
, and the shear-dominated regime for
![]() $\unicode[STIX]{x0394}u>(\unicode[STIX]{x0394}u)_{shear}$
.
$\unicode[STIX]{x0394}u>(\unicode[STIX]{x0394}u)_{shear}$
.
We have also considered alternative variables that are often used in the literature to characterize shear effects, like the flux Richardson number. As observed in figure 18(a), the flux Richardson number at the height of the minimum buoyancy flux captures wind-shear effects as well as the bulk Richardson number, since curves corresponding to different Froude numbers align into a single general curve. However, one disadvantage of using
![]() $(Ri_{f})_{z_{i,f}}$
instead of
$(Ri_{f})_{z_{i,f}}$
instead of
![]() $Ri_{b}$
to characterize wind-shear effects is that
$Ri_{b}$
to characterize wind-shear effects is that
![]() $(Ri_{f})_{z_{i,f}}$
asymptotes towards
$(Ri_{f})_{z_{i,f}}$
asymptotes towards
![]() $\simeq 0.25{-}0.3$
for large Froude numbers (figure 8
b). Hence, properties become very sensitive with respect to
$\simeq 0.25{-}0.3$
for large Froude numbers (figure 8
b). Hence, properties become very sensitive with respect to
![]() $(Ri_{f})_{z_{i,f}}$
, and small errors in determining
$(Ri_{f})_{z_{i,f}}$
, and small errors in determining
![]() $(Ri_{f})_{z_{i,f}}$
can lead to large errors in the diagnosed statistical properties. Another disadvantage of using
$(Ri_{f})_{z_{i,f}}$
can lead to large errors in the diagnosed statistical properties. Another disadvantage of using
![]() $(Ri_{f})_{z_{i,f}}$
to characterize wind-shear effects is that, from a practical point of view, measuring the flux Richardson number at the height of the minimum buoyancy flux requires calculating gradients and covariances, which can be challenging, whereas estimating
$(Ri_{f})_{z_{i,f}}$
to characterize wind-shear effects is that, from a practical point of view, measuring the flux Richardson number at the height of the minimum buoyancy flux requires calculating gradients and covariances, which can be challenging, whereas estimating
![]() $\unicode[STIX]{x0394}u$
, the velocity difference between the free atmosphere and the mixed layer, can be easier.
$\unicode[STIX]{x0394}u$
, the velocity difference between the free atmosphere and the mixed layer, can be easier.
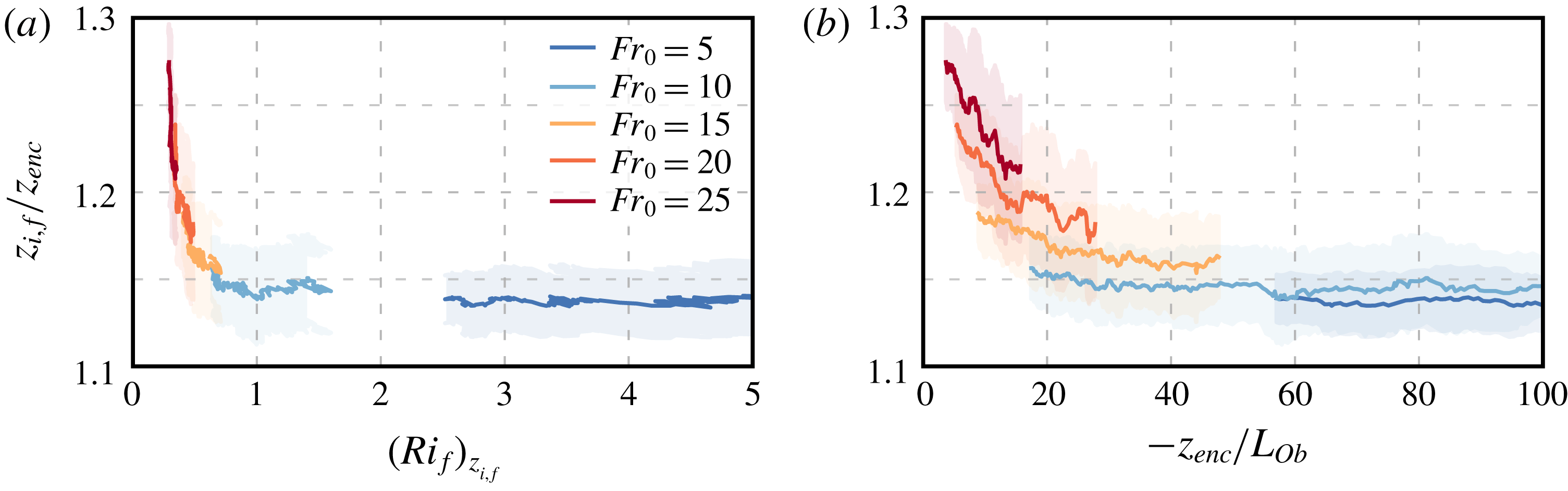
Figure 18. Temporal evolution of the normalized flux-based CBL depth as a function of (a) the flux Richardson number
![]() $(Ri_{f})_{z_{i,f}}$
and (b) the stability parameter
$(Ri_{f})_{z_{i,f}}$
and (b) the stability parameter
![]() $-z_{enc}/L_{Ob}$
.
$-z_{enc}/L_{Ob}$
.
Another variable that we have studied as an alternative independent variable is the stability parameter
![]() $-z_{enc}/L_{Ob}$
, since this variable is often used to characterize wind-shear effects on various properties of CBLs. We plot in figure 18(b) the evolution of the height of the minimum buoyancy flux normalized by the encroachment length scale versus
$-z_{enc}/L_{Ob}$
, since this variable is often used to characterize wind-shear effects on various properties of CBLs. We plot in figure 18(b) the evolution of the height of the minimum buoyancy flux normalized by the encroachment length scale versus
![]() $-z_{enc}/L_{Ob}$
. Curves corresponding to different Froude numbers do not align into a single general curve, and the dependence of the entrainment-zone thickness on
$-z_{enc}/L_{Ob}$
. Curves corresponding to different Froude numbers do not align into a single general curve, and the dependence of the entrainment-zone thickness on
![]() $Fr_{0}$
is of the order of one for
$Fr_{0}$
is of the order of one for
![]() $-z_{enc}/L_{Ob}<20$
. Hence, the stability parameter
$-z_{enc}/L_{Ob}<20$
. Hence, the stability parameter
![]() $-z_{enc}/L_{Ob}$
is insufficient to characterize wind-shear effects on entrainment-zone properties.
$-z_{enc}/L_{Ob}$
is insufficient to characterize wind-shear effects on entrainment-zone properties.
One last aspect that is worth discussing is to what extent DNS studies such as the ones presented here might be representative of the atmospheric CBL, given the disparity of Reynolds numbers between the DNS and the atmospheric CBL. There are properties that might certainly be poorly represented with the Reynolds number that we reach in our simulations. For instance, inertial-range and dissipative-range properties in the entrainment zone are likely to be poorly represented, since the ratio between the Ozmidov scale and the Kolmogorov scale, quantified by
![]() $(Re_{b})^{3/4}$
, is less than 10. However, the entrainment-zone properties addressed in this work, such as second-order moments and the TKE budget equation, show less than 10–20 % sensitivity to the larger Reynolds numbers reached in our simulations – the mean properties and the corresponding layered vertical structure show even less sensitivity. The reason is that much of those properties is determined by the interaction between convection in the mixed layer, which is dominated by large scales, and the mean velocity profile in the entrainment zone, which is also well represented. Hence, even if some of the coefficients in the scaling laws derived in this work might still vary on the order of 10–20 % as the Reynolds number in the DNS is further increased, the functional relationships in those scaling laws are likely robust, and therefore DNS can provide relevant information about the atmospheric CBL. A similar convergence towards Reynolds-number similarity has also been reported in cloud-topped boundary layers, and it is associated with the capability to resolve the Ozmidov scale at the CBL top, and hence resolve wave-like motions, which are very poorly represented by standard down-gradient mixing models (Mellado et al.
Reference Mellado, Bretherton, Stevens and Wyant2018). A more challenging aspect, we believe, is how to transfer the results obtained from idealized studies to the atmospheric context, given the complex interaction of various processes often occurring in the atmospheric CBL.
$(Re_{b})^{3/4}$
, is less than 10. However, the entrainment-zone properties addressed in this work, such as second-order moments and the TKE budget equation, show less than 10–20 % sensitivity to the larger Reynolds numbers reached in our simulations – the mean properties and the corresponding layered vertical structure show even less sensitivity. The reason is that much of those properties is determined by the interaction between convection in the mixed layer, which is dominated by large scales, and the mean velocity profile in the entrainment zone, which is also well represented. Hence, even if some of the coefficients in the scaling laws derived in this work might still vary on the order of 10–20 % as the Reynolds number in the DNS is further increased, the functional relationships in those scaling laws are likely robust, and therefore DNS can provide relevant information about the atmospheric CBL. A similar convergence towards Reynolds-number similarity has also been reported in cloud-topped boundary layers, and it is associated with the capability to resolve the Ozmidov scale at the CBL top, and hence resolve wave-like motions, which are very poorly represented by standard down-gradient mixing models (Mellado et al.
Reference Mellado, Bretherton, Stevens and Wyant2018). A more challenging aspect, we believe, is how to transfer the results obtained from idealized studies to the atmospheric context, given the complex interaction of various processes often occurring in the atmospheric CBL.
7 Summary and conclusions
A systematic analysis of wind-shear effects on barotropic convective boundary layers growing into linearly stratified atmospheres has been carried out by means of dimensional analysis and direct numerical simulation. Dimensional analysis allows us to characterize the system by a normalized CBL depth,
![]() $z_{enc}/L_{0}$
, a Froude number
$z_{enc}/L_{0}$
, a Froude number
![]() $Fr_{0}\equiv U_{0}/(N_{0}L_{0})$
, a reference buoyancy Reynolds number,
$Fr_{0}\equiv U_{0}/(N_{0}L_{0})$
, a reference buoyancy Reynolds number,
![]() $Re_{0}\equiv N_{0}L_{0}^{2}/\unicode[STIX]{x1D708}$
, and the Prandtl number. The first two non-dimensional quantities embed the dependence of the system on time, on the surface buoyancy flux,
$Re_{0}\equiv N_{0}L_{0}^{2}/\unicode[STIX]{x1D708}$
, and the Prandtl number. The first two non-dimensional quantities embed the dependence of the system on time, on the surface buoyancy flux,
![]() $B_{0}$
, and on the wind velocity and the buoyancy stratification in the free atmosphere,
$B_{0}$
, and on the wind velocity and the buoyancy stratification in the free atmosphere,
![]() $U_{0}$
and
$U_{0}$
and
![]() $N_{0}^{2}$
, respectively. The encroachment length scale
$N_{0}^{2}$
, respectively. The encroachment length scale
![]() $z_{enc}$
is a measure of the shear-free CBL depth, and
$z_{enc}$
is a measure of the shear-free CBL depth, and
![]() $L_{0}=(B_{0}/N_{0}^{3})^{1/2}$
is the reference Ozmidov length. Here
$L_{0}=(B_{0}/N_{0}^{3})^{1/2}$
is the reference Ozmidov length. Here
![]() $L_{0}$
and
$L_{0}$
and
![]() $Re_{0}$
characterize the turbulence in the upper sublayer of the entrainment zone, a strongly stratified region that serves as a transition between the CBL and the free atmosphere. The ratio
$Re_{0}$
characterize the turbulence in the upper sublayer of the entrainment zone, a strongly stratified region that serves as a transition between the CBL and the free atmosphere. The ratio
![]() $z_{enc}/L_{0}$
increases as the CBL grows into the linearly stratified atmosphere, and we have focused on the equilibrium (quasi-steady) entrainment regime, when CBL properties evolve on time scales much larger than the eddy turnover time of the large, energy-containing motions. In particular, we have studied the intervals
$z_{enc}/L_{0}$
increases as the CBL grows into the linearly stratified atmosphere, and we have focused on the equilibrium (quasi-steady) entrainment regime, when CBL properties evolve on time scales much larger than the eddy turnover time of the large, energy-containing motions. In particular, we have studied the intervals
![]() $15\lesssim z_{enc}/L_{0}\lesssim 35$
and
$15\lesssim z_{enc}/L_{0}\lesssim 35$
and
![]() $0\leqslant Fr_{0}\leqslant 25$
, which represent typical midday atmospheric conditions over land with wind velocities of up to
$0\leqslant Fr_{0}\leqslant 25$
, which represent typical midday atmospheric conditions over land with wind velocities of up to
![]() $U_{0}\simeq 15~\text{m}~\text{s}^{-1}$
. The Prandtl number has been set to 1. We have thoroughly studied the case
$U_{0}\simeq 15~\text{m}~\text{s}^{-1}$
. The Prandtl number has been set to 1. We have thoroughly studied the case
![]() $Re_{0}=25$
and compared the main results with data from
$Re_{0}=25$
and compared the main results with data from
![]() $Re_{0}=42$
. The observed degree of Reynolds-number similarity indicates that the results found in this study can be informative for atmospheric conditions.
$Re_{0}=42$
. The observed degree of Reynolds-number similarity indicates that the results found in this study can be informative for atmospheric conditions.
We have found that the dependence of mixed-layer and entrainment-zone properties on the normalized CBL depth
![]() $z_{enc}/L_{0}$
and the Froude number
$z_{enc}/L_{0}$
and the Froude number
![]() $Fr_{0}$
can be expressed in terms of one single independent variable,
$Fr_{0}$
can be expressed in terms of one single independent variable,
![]() $(\unicode[STIX]{x0394}z_{i})_{s}/(\unicode[STIX]{x0394}z_{i})_{c}$
, where
$(\unicode[STIX]{x0394}z_{i})_{s}/(\unicode[STIX]{x0394}z_{i})_{c}$
, where
![]() $(\unicode[STIX]{x0394}z_{i})_{s}=\sqrt{1/3}\unicode[STIX]{x0394}u/N_{0}$
is the entrainment-zone scale in weakly unstable conditions (strong wind),
$(\unicode[STIX]{x0394}z_{i})_{s}=\sqrt{1/3}\unicode[STIX]{x0394}u/N_{0}$
is the entrainment-zone scale in weakly unstable conditions (strong wind),
![]() $\unicode[STIX]{x0394}u\equiv U_{0}-u_{ml}$
being the velocity difference between the free atmosphere and the mixed layer, and
$\unicode[STIX]{x0394}u\equiv U_{0}-u_{ml}$
being the velocity difference between the free atmosphere and the mixed layer, and
![]() $(\unicode[STIX]{x0394}z_{i})_{c}=0.25z_{enc}$
is the entrainment-zone scale in strongly unstable conditions (weak wind). The ratio
$(\unicode[STIX]{x0394}z_{i})_{c}=0.25z_{enc}$
is the entrainment-zone scale in strongly unstable conditions (weak wind). The ratio
![]() $(\unicode[STIX]{x0394}z_{i})_{s}/(\unicode[STIX]{x0394}z_{i})_{c}$
increases as the wind velocity increases, and in this study we have considered the range
$(\unicode[STIX]{x0394}z_{i})_{s}/(\unicode[STIX]{x0394}z_{i})_{c}$
increases as the wind velocity increases, and in this study we have considered the range
![]() $0\leqslant (\unicode[STIX]{x0394}z_{i})_{s}/(\unicode[STIX]{x0394}z_{i})_{c}\lesssim 1.5$
, which corresponds to the weakly to strongly unstable conditions
$0\leqslant (\unicode[STIX]{x0394}z_{i})_{s}/(\unicode[STIX]{x0394}z_{i})_{c}\lesssim 1.5$
, which corresponds to the weakly to strongly unstable conditions
![]() $-z_{enc}/L_{Ob}\gtrsim 4$
. The mean buoyancy and the mean buoyancy flux in the mixed layer follow shear-free scaling laws for all those conditions. For
$-z_{enc}/L_{Ob}\gtrsim 4$
. The mean buoyancy and the mean buoyancy flux in the mixed layer follow shear-free scaling laws for all those conditions. For
![]() $(\unicode[STIX]{x0394}z_{i})_{s}/(\unicode[STIX]{x0394}z_{i})_{c}<0.35$
, convection dominates the entrainment-zone dynamics, and wind-shear effects on entrainment-zone properties are negligible. Wind-shear effects on entrainment appear when
$(\unicode[STIX]{x0394}z_{i})_{s}/(\unicode[STIX]{x0394}z_{i})_{c}<0.35$
, convection dominates the entrainment-zone dynamics, and wind-shear effects on entrainment-zone properties are negligible. Wind-shear effects on entrainment appear when
![]() $(\unicode[STIX]{x0394}z_{i})_{s}/(\unicode[STIX]{x0394}z_{i})_{c}\simeq 0.35$
, which corresponds to
$(\unicode[STIX]{x0394}z_{i})_{s}/(\unicode[STIX]{x0394}z_{i})_{c}\simeq 0.35$
, which corresponds to
![]() $\simeq 5~\text{m}~\text{s}^{-1}$
for typical midday conditions, and become of order one when
$\simeq 5~\text{m}~\text{s}^{-1}$
for typical midday conditions, and become of order one when
![]() $(\unicode[STIX]{x0394}z_{i})_{s}/(\unicode[STIX]{x0394}z_{i})_{c}\simeq 0.6$
. The corresponding critical values of
$(\unicode[STIX]{x0394}z_{i})_{s}/(\unicode[STIX]{x0394}z_{i})_{c}\simeq 0.6$
. The corresponding critical values of
![]() $\unicode[STIX]{x0394}u$
are provided in (6.4) and (6.5) in terms of the encroachment CBL depth, the surface buoyancy flux, and the stratification in the free atmosphere.
$\unicode[STIX]{x0394}u$
are provided in (6.4) and (6.5) in terms of the encroachment CBL depth, the surface buoyancy flux, and the stratification in the free atmosphere.
We have rationalized the relevance of the variable
![]() $(\unicode[STIX]{x0394}z_{i})_{s}/(\unicode[STIX]{x0394}z_{i})_{c}$
and the validity of shear-free scaling laws below
$(\unicode[STIX]{x0394}z_{i})_{s}/(\unicode[STIX]{x0394}z_{i})_{c}$
and the validity of shear-free scaling laws below
![]() $(\unicode[STIX]{x0394}z_{i})_{s}/(\unicode[STIX]{x0394}z_{i})_{c}\simeq 0.35$
by analysing the two-layer vertical structure of the entrainment zone. In particular, we have obtained the entrainment-zone scale
$(\unicode[STIX]{x0394}z_{i})_{s}/(\unicode[STIX]{x0394}z_{i})_{c}\simeq 0.35$
by analysing the two-layer vertical structure of the entrainment zone. In particular, we have obtained the entrainment-zone scale
![]() $\unicode[STIX]{x0394}z_{i}$
that characterizes the lower entrainment-zone sublayer. The limit of
$\unicode[STIX]{x0394}z_{i}$
that characterizes the lower entrainment-zone sublayer. The limit of
![]() $\unicode[STIX]{x0394}z_{i}$
for vanishingly weak wind is
$\unicode[STIX]{x0394}z_{i}$
for vanishingly weak wind is
![]() $(\unicode[STIX]{x0394}z_{i})_{c}$
, and the limit of
$(\unicode[STIX]{x0394}z_{i})_{c}$
, and the limit of
![]() $\unicode[STIX]{x0394}z_{i}$
for strong wind is
$\unicode[STIX]{x0394}z_{i}$
for strong wind is
![]() $(\unicode[STIX]{x0394}z_{i})_{s}$
. The variable
$(\unicode[STIX]{x0394}z_{i})_{s}$
. The variable
![]() $(\unicode[STIX]{x0394}z_{i})_{s}$
can be interpreted as the asymptotic thickness of a stably stratified shear layer that would form in the limit of strong wind. Hence, as wind shear increases and the variable
$(\unicode[STIX]{x0394}z_{i})_{s}$
can be interpreted as the asymptotic thickness of a stably stratified shear layer that would form in the limit of strong wind. Hence, as wind shear increases and the variable
![]() $(\unicode[STIX]{x0394}z_{i})_{s}/(\unicode[STIX]{x0394}z_{i})_{c}$
increases, the value
$(\unicode[STIX]{x0394}z_{i})_{s}/(\unicode[STIX]{x0394}z_{i})_{c}$
increases, the value
![]() $\simeq 0.35$
can be interpreted as the condition at which the characteristic length scale in the lower entrainment-zone sublayer
$\simeq 0.35$
can be interpreted as the condition at which the characteristic length scale in the lower entrainment-zone sublayer
![]() $\unicode[STIX]{x0394}z_{i}$
changes from the convective limit
$\unicode[STIX]{x0394}z_{i}$
changes from the convective limit
![]() $(\unicode[STIX]{x0394}z_{i})_{c}$
towards the shear limit
$(\unicode[STIX]{x0394}z_{i})_{c}$
towards the shear limit
![]() $(\unicode[STIX]{x0394}z_{i})_{s}$
. Consistently, the analysis of the budget of the TKE shows that, at this condition, shear production becomes comparable to turbulent transport as a source of TKE in the entrainment zone. The corresponding flux Richardson number
$(\unicode[STIX]{x0394}z_{i})_{s}$
. Consistently, the analysis of the budget of the TKE shows that, at this condition, shear production becomes comparable to turbulent transport as a source of TKE in the entrainment zone. The corresponding flux Richardson number
![]() $Ri_{f}\equiv -\langle b^{\prime }w^{\prime }\rangle /P$
particularized at
$Ri_{f}\equiv -\langle b^{\prime }w^{\prime }\rangle /P$
particularized at
![]() $z_{i,f}$
at this state is
$z_{i,f}$
at this state is
![]() $\simeq 1$
, instead of the value
$\simeq 1$
, instead of the value
![]() $\simeq 0.25{-}0.3$
characteristic of marginally stable stratified shear layers: the value
$\simeq 0.25{-}0.3$
characteristic of marginally stable stratified shear layers: the value
![]() $\simeq 0.25{-}0.3$
is recovered when we subtract the buoyancy flux of the shear-free limit from the numerator. The upper entrainment-zone sublayer is characterized by the Ozmidov scale evaluated at the height of the minimum buoyancy flux. As the turbulence intensity in the lower entrainment-zone sublayer increases with respect to shear-free conditions, the lower entrainment-zone sublayer broadens and so does the upper entrainment-zone sublayer.
$\simeq 0.25{-}0.3$
is recovered when we subtract the buoyancy flux of the shear-free limit from the numerator. The upper entrainment-zone sublayer is characterized by the Ozmidov scale evaluated at the height of the minimum buoyancy flux. As the turbulence intensity in the lower entrainment-zone sublayer increases with respect to shear-free conditions, the lower entrainment-zone sublayer broadens and so does the upper entrainment-zone sublayer.
The reduction of the number of independent variables from two to one can help simplify the parametrization of mixed-layer and entrainment-zone properties in atmospheric models. To this aim, we have provided scaling laws for the reference heights in (4.12), for the entrainment-zone scale in (5.11), for the Ozmidov length in (5.17) and for the entrainment-flux ratio in (5.14), in terms of
![]() $B_{0}$
,
$B_{0}$
,
![]() $N_{0}$
,
$N_{0}$
,
![]() $\unicode[STIX]{x0394}u$
and time. Such a reduction from two independent variables to one can also be expressed in terms of the bulk Richardson number
$\unicode[STIX]{x0394}u$
and time. Such a reduction from two independent variables to one can also be expressed in terms of the bulk Richardson number
![]() $Ri_{b}\equiv N_{0}^{2}z_{enc}^{2}/(\unicode[STIX]{x0394}u)^{2}$
, but not in terms of the stability parameter
$Ri_{b}\equiv N_{0}^{2}z_{enc}^{2}/(\unicode[STIX]{x0394}u)^{2}$
, but not in terms of the stability parameter
![]() $-z_{enc}/L_{Ob}$
.
$-z_{enc}/L_{Ob}$
.
Acknowledgements
The authors gratefully acknowledge the Gauss Centre for Supercomputing (GCS) for providing computing time through the John von Neumann Institute for Computing (NIC) on the GCS share of the supercomputer JUQUEEN at Jülich Supercomputing Centre (JSC). Funding was provided by the Max Planck Society through its Max Planck Research Groups programme. Primary data and scripts used in the analysis and other supporting information that may be useful in reproducing the author’s work are archived by the Max Planck Institute for Meteorology and can be obtained by contacting [email protected].
Appendix A. Entrainment-rate equation
To derive the entrainment-rate equation based on the mean buoyancy, we integrate the evolution equation of the mean buoyancy relative to the reference background profile
from
![]() $z_{i,f}$
upwards. Applying the Leibniz rule yields
$z_{i,f}$
upwards. Applying the Leibniz rule yields
which can be rearranged to obtain the entrainment rate equation
Garcia & Mellado (Reference Garcia and Mellado2014) have shown that the distortion term (the integral term in A 3) is relatively small. Therefore, for Reynolds numbers that are large enough to neglect the molecular-flux terms, the turbulent buoyancy flux at
![]() $z_{i,f}$
is approximately equal to
$z_{i,f}$
is approximately equal to
![]() $[N_{0}^{2}z-\langle b\rangle ]_{z_{i,f}}\text{d}_{t}z_{i,f}$
. Concomitantly, figure 19(a) shows that
$[N_{0}^{2}z-\langle b\rangle ]_{z_{i,f}}\text{d}_{t}z_{i,f}$
. Concomitantly, figure 19(a) shows that
![]() $[N_{0}^{2}z-\langle b\rangle ]_{z_{i,f}}$
, which is the local deviation of the mean profile with respect to the background profile
$[N_{0}^{2}z-\langle b\rangle ]_{z_{i,f}}$
, which is the local deviation of the mean profile with respect to the background profile
![]() $b_{0}$
at the height
$b_{0}$
at the height
![]() $z_{i,f}$
, is well scaled by
$z_{i,f}$
, is well scaled by
![]() $N_{0}^{2}\unicode[STIX]{x0394}z_{i}$
. As a result, the entrainment-rate equation based on the mean buoyancy provides the scaling law
$N_{0}^{2}\unicode[STIX]{x0394}z_{i}$
. As a result, the entrainment-rate equation based on the mean buoyancy provides the scaling law
![]() $-\langle b^{\prime }w^{\prime }\rangle _{z_{i,f}}\sim w_{e}N_{0}^{2}\unicode[STIX]{x0394}z_{i}$
, where
$-\langle b^{\prime }w^{\prime }\rangle _{z_{i,f}}\sim w_{e}N_{0}^{2}\unicode[STIX]{x0394}z_{i}$
, where
![]() $w_{e}\equiv \text{d}_{t}z_{i,f}$
.
$w_{e}\equiv \text{d}_{t}z_{i,f}$
.
The same analysis is carried out to derive the entrainment-rate equation based on the mean velocity
The contribution of the distortion term compared to the contribution of the kinematic momentum flux at
![]() $z_{i,f}$
is small, which implies that
$z_{i,f}$
is small, which implies that
![]() $-\langle u^{\prime }w^{\prime }\rangle _{z_{i,f}}$
is approximately equal to
$-\langle u^{\prime }w^{\prime }\rangle _{z_{i,f}}$
is approximately equal to
![]() $[U_{0}-\langle u\rangle ]_{z_{i,f}}\text{d}_{t}z_{i,f}$
for a large enough
$[U_{0}-\langle u\rangle ]_{z_{i,f}}\text{d}_{t}z_{i,f}$
for a large enough
![]() $Re_{0}$
. Figure 19(b) shows that
$Re_{0}$
. Figure 19(b) shows that
![]() $[U_{0}-\langle u\rangle ]_{z_{i,f}}$
is well scaled by
$[U_{0}-\langle u\rangle ]_{z_{i,f}}$
is well scaled by
![]() $\unicode[STIX]{x0394}u$
, the velocity increment across the entrainment zone defined by (4.7). Therefore, the entrainment-rate equation based on the mean velocity provides the scaling law
$\unicode[STIX]{x0394}u$
, the velocity increment across the entrainment zone defined by (4.7). Therefore, the entrainment-rate equation based on the mean velocity provides the scaling law
![]() $-\langle u^{\prime }w^{\prime }\rangle _{z_{i,f}}\sim w_{e}\unicode[STIX]{x0394}u$
.
$-\langle u^{\prime }w^{\prime }\rangle _{z_{i,f}}\sim w_{e}\unicode[STIX]{x0394}u$
.
The entrainment-rate equations derived above recover the jump relations used in mixed-layer models when the mixed-layer model approximations to the actual solutions are substituted into them (Fedorovich et al.
Reference Fedorovich, Conzemius and Mironov2004b
). With this mixed-layer approximation, the increments
![]() $[N_{0}^{2}z-\langle b\rangle ]_{z_{i,f}}$
and
$[N_{0}^{2}z-\langle b\rangle ]_{z_{i,f}}$
and
![]() $[U_{0}-\langle u\rangle ]_{z_{i,f}}$
coincide with the jumps of buoyancy and velocity across the CBL top. However, when the entrainment-rate equations are applied to the actual solutions of the governing equations (2.1), those increments are not the difference between two arbitrary heights at the CBL top, but have a very specific definition, namely, the difference between the reference background profiles and the mean values at the particular height chosen to track the CBL top, in this case, the height of minimum buoyancy flux.
$[U_{0}-\langle u\rangle ]_{z_{i,f}}$
coincide with the jumps of buoyancy and velocity across the CBL top. However, when the entrainment-rate equations are applied to the actual solutions of the governing equations (2.1), those increments are not the difference between two arbitrary heights at the CBL top, but have a very specific definition, namely, the difference between the reference background profiles and the mean values at the particular height chosen to track the CBL top, in this case, the height of minimum buoyancy flux.