Article contents
Characterization of very-large-scale motions in supersonic and hypersonic turbulent boundary layers
Published online by Cambridge University Press: 26 January 2024
Abstract
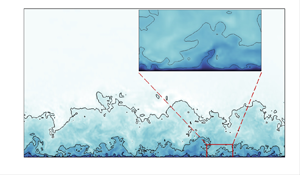
Very-large-scale motions are commonly observed in moderate- and high-Reynolds-number wall turbulence, constituting a considerable portion of the Reynolds stress and skin friction. This study aims to investigate the behaviour of these motions in high-speed and high-Reynolds-number turbulent boundary layers at varying Mach numbers. With the aid of high-precision numerical simulations, numerical experiments and theoretical analysis, it is demonstrated that the very-large-scale motions are weakened in high-Mach-number turbulence at the same friction Reynolds numbers, leading to the reduction in turbulent kinetic energy in the outer region. Conversely, the lower wall temperature enhances the very-large-scale motions but shortens the scale separation between the structures in the near-wall and outer regions.
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press
References
- 5
- Cited by



