Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-30T20:49:05.471Z Has data issue: false hasContentIssue false
  • English
  • Français

Characteristics of the leading Lyapunov vector in a turbulent channel flow

Published online by Cambridge University Press:  26 June 2018

Nikolay Nikitin Open the ORCID record for Nikolay Nikitin [Opens in a new window]
Nikolay Nikitin*
Affiliation:
Institute of Mechanics, Lomonosov Moscow State University, 1 Michurinsky prospect, 119899 Moscow, Russia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The values of the highest Lyapunov exponent (HLE) 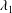$\unicode[STIX]{x1D706}_{1}$ for turbulent flow in a plane channel at Reynolds numbers up to 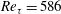$Re_{\unicode[STIX]{x1D70F}}=586$ are determined. The instantaneous and statistical properties of the corresponding leading Lyapunov vector (LLV) are investigated. The LLV is calculated by numerical solution of the Navier–Stokes equations linearized about the non-stationary base solution corresponding to the developed turbulent flow. The base turbulent flow is calculated in parallel with the calculation of the evolution of the perturbations. For arbitrary initial conditions, the regime of exponential growth 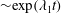${\sim}\exp (\unicode[STIX]{x1D706}_{1}t)$ which corresponds to the approaching of the perturbation to the LLV is achieved already at 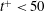$t^{+}<50$. It is found that the HLE increases with increasing Reynolds number from 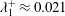$\unicode[STIX]{x1D706}_{1}^{+}\approx 0.021$ at 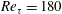$Re_{\unicode[STIX]{x1D70F}}=180$ to 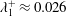$\unicode[STIX]{x1D706}_{1}^{+}\approx 0.026$ at 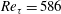$Re_{\unicode[STIX]{x1D70F}}=586$. The LLV structures are concentrated mainly in a region of the buffer layer and are manifested in the form of spots of increased fluctuation intensity localized both in time and space. The root-mean-square (r.m.s.) profiles of the velocity and vorticity intensities in the LLV are qualitatively close to the corresponding profiles in the base flow with artificially removed near-wall streaks. The difference is the larger concentration of LLV perturbations in the vicinity of the buffer layer and a relatively larger (by approximately 80 %) amplitude of the vorticity pulsations. Based on the energy spectra of velocity and vorticity pulsations, the integral spatial scales of the LLV structures are determined. It is found that LLV structures are on average twice narrower and twice shorter than the corresponding structures of the base flow. The contribution of each of the terms entering into the expression for the production of the perturbation kinetic energy is determined. It is shown that the process of perturbation development is essentially dictated by the inhomogeneity of the base flow, as well as by the presence of transversal motion in it. Neglecting of these factors leads to a significant underestimation of the perturbation growth rate. The presence of near-wall streaks in the base flow, on the contrary, does not play a significant role in the development of the LLV perturbations. Artificial removal of streaks from the base flow does not change the character of the perturbation growth.

JFM classification

Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulent boundary layers
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 849 , 25 August 2018 , pp. 942 - 967
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Brooke, J. W. & Hanratty, T. J. 1993 Origin of turbulence producing eddies in a channel flow. Phys. Fluids A 5, 1011–1021.Google Scholar
Butler, K. M. & Farrell, B. F. 1992 Three-dimensional optimal disturbances in viscous shear flow. Phys. Fluids A 4, 1637–1650.Google Scholar
Butler, K. M. & Farrell, B. F. 1993 Optimal perturbations and streak spacing in wall-bounded turbulent shear flows. Phys. Fluids A 5, 774–777.Google Scholar
Chernyshenko, S. I. & Baig, M. F. 2005 The mechanism of streak formation in near-wall turbulence. J. Fluid Mech. 544, 99–131.Google Scholar
Del Álamo, J. C. & Jiménez, J. 2006 Linear energy amplification in turbulent channels. J. Fluid Mech. 559, 205–213.Google Scholar
Durbin, P. & Wu, X. 2007 Transition beneath vortical disturbances. Annu. Rev. Fluid Mech. 39, 107–128.Google Scholar
Egolf, D. A., Melnikov, I. V., Pesch, W. & Ecke, R. E. 2000 Mechanisms of extensive spatiotemporal chaos in Rayleigh–Bénard convection. Nature 404, 733–736.Google Scholar
Farano, M., Cherubini, S., Robinet, J.-C. & De Palma, P. 2017 Optimal bursts in turbulent channel flow. J. Fluid Mech. 817, 35–60.Google Scholar
Farrell, B. F. & Ioannou, P. J. 1996 Generalized stability. Part II. Non-autonomous operators. J. Atmos. Sci. 53, 2041–2053.Google Scholar
Farrell, B. F. & Ioannou, P. J. 2012 Dynamics of streamwise rolls and streaks in turbulent wall-bounded shear flow. J. Fluid Mech. 708, 149–196.Google Scholar
Farrell, B. F., Ioannou, P. J., Jiménez, J., Constantinou, N. C., Lozano-Durán, A. & Nikolaidis, M.-A. 2016 A statistical state dynamics-based study of the structure and mechanism of large-scale motions in plane Poiseuille flow. J. Fluid Mech. 809, 290–315.Google Scholar
Ginelli, F., Poggi, P., Turchi, A., Chate, H., Livi, R. & Politi, A. 2007 Characterizing dynamics with covariant Lyapunov vectors. Phys. Rev. Lett. 99, 130601.Google Scholar
Hamilton, K., Kim, J. & Waleffe, F. 1995 Regeneration mechanisms of near-wall turbulence structures. J. Fluid Mech. 287, 317–348.Google Scholar
Hutchins, N. & Marusic, I. 2007 Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.Google Scholar
Inubushi, M., Takehiro, S.-i. & Yamada, M. 2015 Regeneration cycle and the covariant Lyapunov vectors in a minimal wall turbulence. Phys. Rev. E 92, 023022.Google Scholar
Jang, P. S., Benney, D. J. & Gran, R. L. 1986 On the origin of streamwise vortices in a turbulent boundary layer. J. Fluid Mech. 169, 109–123.Google Scholar
Jayaraman, A., Scheel, J. D., Greenside, H. S. & Fischer, P. F. 2006 Characterization of the domain chaos convection state by the largest Lyapunov exponent. Phys. Rev. E 74, 016209.Google Scholar
Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.Google Scholar
Jeong, J., Hussain, F., Schoppa, W. & Kim, J. 1997 Coherent structures near the wall in a turbulent channel flow. J. Fluid Mech. 332, 185–214.Google Scholar
Jimenez, J. & Pinelli, A. 1999 The autonomous cycle of near wall turbulence. J. Fluid Mech. 389, 335–359.Google Scholar
Kawahara, G., Jiménez, J., Uhlmann, M. & Pinelli, A.1998 The instability of streaks in near-wall turbulence. CTR Annu. Res. Briefs, Stanford University, pp. 155–170.Google Scholar
Keefe, L., Moin, P. & Kim, J. 1992 The dimension of attractors underlying periodic turbulent Poiseuille flow. J. Fluid Mech. 242, 1–29.Google Scholar
Kim, J. & Hussain, F. 1993 Propagation velocity of perturbations in turbulent channel flow. Phys. Fluids A 5, 695–706.Google Scholar
Kim, H. T., Kline, S. J. & Reynolds, W. C. 1971 The production of turbulence near a smooth wall in a turbulent boundary layers. J. Fluid Mech. 50, 133–160.Google Scholar
Klebanoff, P. S., Tidstrom, K. D. & Sargent, L. M. 1962 The three-dimensional nature of boundary-layer instability. J. Fluid Mech. 12, 1–34.Google Scholar
Kline, S. J., Reynolds, W. C., Schraub, F. A. & Runstadler, P. W. 1967 The structure of turbulent boundary layers. J. Fluid Mech. 30, 741–773.Google Scholar
Landahl, M. T. 1980 A note on an algebraic instability of inviscid parallel shear flows. J. Fluid Mech. 98, 243–251.Google Scholar
Matsubara, M. & Alfredsson, P. 2001 Disturbance growth in boundary layers subjected to free-stream turbulence. J. Fluid Mech. 430, 149–168.Google Scholar
Moser, R. D., Kim, J. & Mansour, N. N. 1999 Direct numerical simulation of turbulent channel flow up to Re 𝜏 = 590. Phys. Fluids 11 (4), 943–945.Google Scholar
Nikitin, N. 2006 Finite-difference method for incompressible Navier–Stokes equations in arbitrary orthogonal curvilinear coordinates. J. Comput. Phys. 217, 759–781.Google Scholar
Nikitin, N. 2007 Spatial periodicity of spatially evolving turbulent flow caused by inflow boundary condition. Phys. Fluids 19 (9), 091703-4.Google Scholar
Nikitin, N. 2008 On the rate of spatial predictability in near-wall turbulence. J. Fluid Mech. 614, 495–507.Google Scholar
Nikitin, N. V. 2009 Disturbance growth rate in turbulent wall flows. Fluid Dyn. 44 (5), 652–657.Google Scholar
Nikitin, N. V. & Chernyshenko, S. I. 1997 On the nature of the organized structures in turbulent near-wall flows. Fluid Dyn. 32, 18–23.Google Scholar
Nikitin, N. V. & Pivovarov, D. E.2018 On the rate of disturbance growth in turbulent Couette flow. Fluid Dyn. (submitted).Google Scholar
Parker, T. S. & Chua, L. O. 1989 Practical Numerical Algorithms for Chaotic Systems. Springer.Google Scholar
Reddy, S. C. & Henningson, D. S. 1993 Energy growth in viscous shear flows. J. Fluid Mech. 252, 209–238.Google Scholar
Schmid, P. J. & Henningson, D. S. 2001 Stability and Transition in Shear Flows. Springer.Google Scholar
Schoppa, W. & Hussain, F. 1997 Genesis and dynamics of coherent structures in near-wall turbulence: a new look. In Self-Sustaining Mechanisms of Wall Turbulence (ed. Panton, R.), pp. 385–422. Computational Mechanics Publications.Google Scholar
Schoppa, W. & Hussain, F.1998 Formation of near-wall streamwise vortices by streak instability. AIAA Paper 98-3000.Google Scholar
Schoppa, W. & Hussain, F. 2002 Coherent structure generation in near-wall turbulence. J. Fluid Mech. 453, 57–108.Google Scholar
Smith, C. R. & Metzler, S. P. 1983 The characteristics of low-speed streaks in the near-wall region of a turbulent boundary layer. J. Fluid Mech. 129, 27–54.Google Scholar
Sreenivasan, K. R. 1988 A unified view of the origin and morphology of the turbulent boundary layer structure. In Proceedings of the IUTAM Symposium on Turbulence Management and Relaminarisation (ed. Liepmann, H. W. & Narasimha, R.), pp. 37–61. Springer.Google Scholar
Swearingen, J. D. & Blackwelder, R. F. 1987 The growth and breakdown of streamwise vortices in the presence of a wall. J. Fluid Mech. 182, 255–290.Google Scholar
Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. p. 300. MIT Press.Google Scholar
Trefethen, L. N., Trefethen, A. E., Reddy, S. C. & Driscoll, T. A. 1993 Hydrodynamic stability without eigenvalues. Science 261, 578–584.Google Scholar
Unnikrishnan, S. & Gaitonde, D. V. 2016 A high-fidelity method to analyze perturbation evolution in turbulent flows. J. Comput. Phys. 310, 45–62.Google Scholar
Waleffe, F. 1995 Hydrodynamic stability and turbulence: beyond transients to a self-sustaining process. Stud. Appl. Maths 95, 319–343.Google Scholar
Waleffe, F. 1997 On a self-sustaining process in shear flows. Phys. Fluids 9, 883–900.Google Scholar
Waleffe, F. 2003 Homotopy of exact coherent structures in plane shear flows. Phys. Fluids 6, 1517–1534.Google Scholar
Waleffe, F. & Kim, J. 1997 How streamwise rolls and streaks self-sustain in a shear flow. In Self-Sustaining Mechanisms of Wall Turbulence (ed. Panton, R.), pp. 309–332. Computational Mechanics Publications.Google Scholar
Waleffe, F., Kim, J. & Hamilton, J. 1993 On the origin of streaks in turbulent boundary layers. In Turbulent Shear Flows 8 (ed. Durst, F., Friedrich, R., Launder, B. E., Schmidt, F. W., Schumann, U. & Whitelaw, J.), pp. 37–49. Springer.Google Scholar
Westin, K. J. A., Boiko, A. V., Klingmann, B. G. B., Kozlov, V. V. & Alfredsson, P. H. 1994 Experiments in a boundary layer subjected to freestream turbulence. Part I: Boundary layer structure and receptivity. J. Fluid Mech. 281, 193–218.Google Scholar
Wu, X., Moin, P., Wallace, J. M., Skarda, J., Lozano-Duran, A. & Hickey, J.-P. 2017 Transitional-turbulent spots and turbulent–turbulent spots in boundary layers. Proc. Natl Acad. Sci. USA 114 (27), E5292–E5299.Google Scholar
Xu, M. & Paul, M. R. 2016 Covariant Lyapunov vectors of chaotic Rayleigh–Bénard convection. Phys. Rev. E 93, 062208.Google Scholar
Zaki, T. A. 2013 From streaks to spots and on to turbulence: exploring the dynamics of boundary layer transition. Flow Turbul. Combust. 91, 451–473.Google Scholar