Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-24T14:47:50.144Z Has data issue: false hasContentIssue false
  • English
  • Français

Characterisation of drag and wake properties of canopy patches immersed in turbulent boundary layers

Published online by Cambridge University Press:  31 May 2016

S. Taddei ,
C. Manes  and
B. Ganapathisubramani
S. Taddei*
Affiliation:
Water and Environmental Engineering Group, University of Southampton, University Road, Southampton SO17 1BJ, UK Aerodynamics and Flight Mechanics Group, University of Southampton, University Road, Southampton SO17 1BJ, UK
C. Manes
Affiliation:
Politecnico di Torino, Corso Duca degli Abruzzi, 24, 10129, Torino, Italy
B. Ganapathisubramani
Affiliation:
Aerodynamics and Flight Mechanics Group, University of Southampton, University Road, Southampton SO17 1BJ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

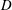The wakes and the drag forces of canopy patches with different densities, immersed in turbulent boundary layers, are investigated experimentally. The patches are circular (with outer diameter $D$) and are made of several identical circular cylinders (height, 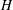$H$, and diameter, 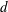$d$). The bulk aspect ratio of all of the patches (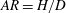$AR=H/D$) was fixed at 1 and the patch density (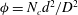${\it\phi}=N_{c}d^{2}/D^{2}$, also referred to as the solidity) is altered by varying the number of cylinders (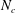$N_{c}$) in the patch. Drag measurements show that the patch drag coefficient increases with increasing density. However, the drag coefficient of the highest investigated density (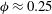${\it\phi}\approx 0.25$) is greater than the drag coefficient of a solid patch (i.e. 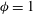${\it\phi}=1$, which is a solid cylinder with 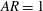$AR=1$). Particle image velocimetry (PIV) measurements were carried out along the streamwise–wall-normal ($x$–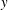$y$) plane along the centreline of patch and in the streamwise–spanwise ($x$–$z$) plane at its mid height (i.e. 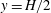$y=H/2$). Mean velocity fields show that the porosity of the patch promotes bleeding along all directions. It was observed that bleeding along the vertical/horizontal direction increases/decreases with increasing 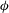${\it\phi}$. Furthermore, it was also observed that bleeding along the lateral direction dictates the point of flow separation along the sides of the patch and makes it independent of ${\it\phi}$. All of these aspects make wakes for porous patches markedly different from their solid counterpart and provide a rational basis to explain the observed trends in the drag coefficient.

JFM classification

Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulent Flows Wakes/Jets: Wakes
Type
Papers
Information
Journal of Fluid Mechanics , Volume 798 , 10 July 2016 , pp. 27 - 49
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Armstrong, G. S., Aprahamian, M. W., Fewings, G. A., Gough, P. J., Reader, N. A. & Varallo, P. V.2010 Document geho 0910 btbp-e-e. Environment Agency Fish Pass Manual.Google Scholar
Ball, D. J., Stansby, P. K. & Alliston, N. 1996 Modelling shallow water flow around pile groups. Proc. Inst. Civ. Eng.-Water 118, 226–236.Google Scholar
Cassiani, M., Katul, G. G. & Albertson, J. D. 2008 The effects of canopy leaf area index on airflow across forest edges: large-eddy simulation and analytical results. Boundary-Layer Meteorol. 126, 433–460.CrossRefGoogle Scholar
Castro, I. P. 1971 Wake characteristics of two-dimensional perforated plates normal to an air-stream. J. Fluid Mech. 46, 599–609.CrossRefGoogle Scholar
Castro, I. P. & Robins, G. 1977 The flow around a surface-mounted cube in uniform and turbulent streams. J. Fluid Mech. 79, 307–335.CrossRefGoogle Scholar
Chang, K. & Constantinescu, G. 2015 Numerical investigation of flow and turbulence structure through and around a circular array of rigid cylinders. J. Fluid Mech. 776, 161–199.Google Scholar
Chen, Z., Ortiz, A., Zong, L. & Nepf, H. 2012 The wake structure behind a porous obstruction and its implications for deposition near a finite patch of emergent vegetation. Water Resour. Res. 48, W09517.CrossRefGoogle Scholar
Flack, K. A., Schultz, M. P. & Connelly, J. S. 2007 Examination of critical roughness height for outer layer similarity. Phys. Fluids 19, 095104.Google Scholar
Flack, K. A., Schultz, M. P. & Shapiro, T. A. 2005 Experimental support for Townsend’s Reynolds number similarity hypothesis on rough walls. Phys. Fluids 17, 035102.Google Scholar
Fox, T. A. & West, G. S. 1993 Fluid-induced loading of cantilevered circular cylinders in a low-turbulence uniform flow. Part 1: mean loading with aspect ratios in the range 4 to 30. J. Fluids Struct. 7, 1–14.Google Scholar
Huang, J., Cassiani, M. & Albertson, J. D. 2011 Coherent turbulent structures across a vegetation discontinuity. Boundary-Layer Meteorol. 140, 1–22.Google Scholar
Irvine, M. R., Gardiner, B. A. & Hill, M. K. 1997 The evolution of turbulence across a forest edge. Boundary-Layer Meteorol. 84, 467–496.CrossRefGoogle Scholar
Manes, C., Poggi, D. & Ridolfi, L. 2011a Turbulent boundary layers over permeable walls: scaling and near wall structure. J. Fluid Mech. 687, 141–170.CrossRefGoogle Scholar
Manes, C., Pokrajac, D., Nikora, V. I., Ridolfi, L. & Poggi, D. 2011b Turbulent friction in flows over permeable walls. Geophys. Res. Lett. 38, L03402.CrossRefGoogle Scholar
Manes, C., Ridolfi, L. & Katul, G. 2012 A phenomenological model to describe turbulent friction in permeable-wall flows. Geophys. Res. Lett. 39, L14403.CrossRefGoogle Scholar
Myers, L. E. & Bhaj, A. S. 2012 An experimental investigation simulating flow effects in first generation marine current energy converter arrays. Renew. Energ. 37, 28–36.CrossRefGoogle Scholar
Nepf, H. M. 2011 Flow over and through biota. In Water and Fine-Sediment Circulation (ed. Wolanski, E. & McLusky, D.), Treatise on Estuarine and Coastal Science, vol. 2, pp. 267–288. Academic.Google Scholar
Nepf, H. M. 2012 Flow and transport in regions with acquatic vegetation. Annu. Rev. Fluid Mech. 44, 123–142.CrossRefGoogle Scholar
Nicolle, A. & Eames, I. 2011 Numerical study of flow through and around a circular array of cylinders. J. Fluid Mech. 679, 1–31.CrossRefGoogle Scholar
Perry, A. E. & Li, J. D. 1990 Experimental support for the attached-eddy hypothesis in zero-pressure-gradient turbulent boundary layers. J. Fluid Mech. 218, 405–438.Google Scholar
Sumner, D. 2013 Flow above the free end of a surface-mounted finite-height circular cylinder: a review. J. Fluids Struct. 43, 41–63.CrossRefGoogle Scholar
Vennell, R. 2010 Tuning turbines in a tidal channel. J. Fluid Mech. 663, 235–267.Google Scholar
Vennell, R. 2011 Tuning tidal turbines in-concert to maximise farm efficiency. J. Fluid Mech. 671, 587–604.Google Scholar
Wang, X. K., Gong, K., Zhang, J.-X. & Tan, S. K. 2013 Flow around four cylinders arranged in a square configuration. J. Fluids Struct. 43, 179–199.CrossRefGoogle Scholar
Zong, L. & Nepf, H. 2012 Vortex development behind a finite porous obstruction in a channel. J. Fluid Mech. 691, 368–391.Google Scholar