Hostname: page-component-5f745c7db-szhh2 Total loading time: 0 Render date: 2025-01-06T21:04:09.047Z Has data issue: true hasContentIssue false
  • English
  • Français

Chaotic advection in a steady, three-dimensional, Ekman-driven eddy

Published online by Cambridge University Press:  05 December 2013

L. J. Pratt ,
I. I. Rypina ,
T. M. Özgökmen ,
P. Wang ,
H. Childs  and
Y. Bebieva
L. J. Pratt*
Affiliation:
Woods Hole Oceanographic Institution, Woods Hole, MA 02543, USA
I. I. Rypina
Affiliation:
Woods Hole Oceanographic Institution, Woods Hole, MA 02543, USA
T. M. Özgökmen
Affiliation:
Rosenstiel School of Marine and Atmospheric Science, University of Miami, Miami, FL, 33149-1098, USA
P. Wang
Affiliation:
Rosenstiel School of Marine and Atmospheric Science, University of Miami, Miami, FL, 33149-1098, USA
H. Childs
Affiliation:
Lawrence Berkeley National Laboratory, CA 94720, USA
Y. Bebieva
Affiliation:
Graduate School of Arts and Science, Yale University, New Haven, CT, 06520, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate and quantify stirring due to chaotic advection within a steady, three-dimensional, Ekman-driven, rotating cylinder flow. The flow field has vertical overturning and horizontal swirling motion, and is an idealization of motion observed in some ocean eddies. The flow is characterized by strong background rotation, and we explore variations in Ekman and Rossby numbers, 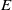$E$ and 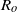${R}_{o} $, over ranges appropriate for the ocean mesoscale and submesoscale. A high-resolution spectral element model is used in conjunction with linear analytical theory, weakly nonlinear resonance analysis and a kinematic model in order to map out the barriers, manifolds, resonance layers and other objects that provide a template for chaotic stirring. As expected, chaos arises when a radially symmetric background state is perturbed by a symmetry-breaking disturbance. In the background state, each trajectory lives on a torus and some of the latter survive the perturbation and act as barriers to chaotic transport, a result consistent with an extension of the KAM theorem for three-dimensional, volume-preserving flow. For shallow eddies, where $E$ is 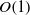$O(1)$, the flow is dominated by thin resonant layers sandwiched between KAM-type barriers, and the stirring rate is weak. On the other hand, eddies with moderately small 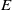$E$ experience thicker resonant layers, wider-spread chaos and much more rapid stirring. This trend reverses for sufficiently small 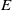$E$, corresponding to deep eddies, where the vertical rigidity imposed by strong rotation limits the stirring. The bulk stirring rate, estimated from a passive tracer release, confirms the non-monotonic variation in stirring rate with 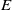$E$. This result is shown to be consistent with linear Ekman layer theory in conjunction with a resonant width calculation and the Taylor–Proudman theorem. The theory is able to roughly predict the value of 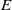$E$ at which stirring is maximum. For large disturbances, the stirring rate becomes monotonic over the range of Ekman numbers explored. We also explore variation in the eddy aspect ratio.

JFM classification

Mixing: Chaotic advection Geophysical and Geological Flows: Geophysical and Geological Flows Geophysical and Geological Flows: Ocean processes
Type
Papers
Information
Journal of Fluid Mechanics , Volume 738 , 10 January 2014 , pp. 143 - 183
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aref, H. 1984 Stirring by chaotic advection. J. Fluid Mech. 143, 1–21.Google Scholar
Barcilon, V. & Pedlosky, J. 1967 A unified theory of homogeneous and stratified rotating fluids. J. Fluid Mech. 29, 609–621.Google Scholar
Behringer, R. P., Meyers, S. D. & Swinney, H. L. 1991 Chaos and mixing in a geostrophic flow. Phys. Fluids A 3, 1234–1249.CrossRefGoogle Scholar
Beron-Vera, F. J. & Olascoaga, M. J. 2009 An assessment of the importance of chaotic stirring and turbulent mixing in the West Florida Shelf. J. Phys. Oceanogr. 9, 1743–1755.Google Scholar
Branicki, M. & Kirwan, A. D. 2010 Stirring: the Eckart paradigm revisited. Intl J. Engng Sci. 48, 1027–1042.Google Scholar
Cheng, C.-Q. & Sun, Y.-S. 1990 Existence of invarient tori in three-dimensional measure-preserving mappings. Celestial Mech. 47, 275–292.Google Scholar
Chirikov, B. V. 1979 A universal instability of many-dimensional oscillator systems. Phys. Rep. 52, 265–379.Google Scholar
Coulliette, C., Lekien, F., Paduan, J. D., Haller, G. & Marsden, J. E. 2007 Optimal pollution mitigation in Monterey Bay based on coastal radar data and nonlinear dynamics. Environ. Sci. Technol. 41, 6562–6572.CrossRefGoogle ScholarPubMed
Coulliette, C. & Wiggins, W. 2001 Intergyre transport in a wind-driven, quasigeostrophic double gyre: an application of lobe dynamics. Nonlinear Process. Geophys. 8, 69–94.Google Scholar
D’Asaro, E. A. 2003 Performance of autonomous Lagrangian floats. J. Atmos. Ocean. Technol. 20, 896–911.Google Scholar
Deese, H. E., Pratt, L. J. & Helfrich, K. R. 2002 A laboratory model of exchange and mixing between western boundary layers and subbasin recirculation gyres. J. Phys. Oceanogr. 32, 1870–1889.Google Scholar
Del-Castillo-Negrete, D. & Morrison, P. J. 1993 Chaotic transport by Rossby waves in shear flow. Phys. Fluids A 5 (4), 948–965.CrossRefGoogle Scholar
Dijkstra, H. A. & Katsman, C. A. 1997 Temporal variability of the wind-driven quasi-geostrophic double gyre ocean circulation: basic bifurcation diagrams. Geophys. Astrophys. Fluid Dyn. 85, 195–232.Google Scholar
Dombre, T., Frisch, U., Green, J. M., Henon, M., Mehr, A. & Soward, A. M. 1986 Chaotic streamlines of the ABC flows. J. Fluid Mech. 353–391.Google Scholar
Duan, J. Q. & Wiggins, S. 1996 Fluid exchange across a meandering jet with quasi-periodic time variability. J. Phys. Oceanogr. 26, 1176–1188.2.0.CO;2>CrossRefGoogle Scholar
Dullin, H. R. & Meiss, J. D. 2013 Quadratic volume-peserving maps: invariant circles and bifurcations. SIAM J. Appl. Dyn. Syst. 8 (1), 76–128.Google Scholar
Fischer, P. F. 1997 An overlapping Schwarz method for spectral element solution of the incompressible Navier–Stokes equations. J. Comput. Phys. 133, 84–101.CrossRefGoogle Scholar
Fountain, G. O., Khakhar, K. V., Mezic, I. & Ottino, J. M. 2000 Chaotic mixing in a bounded three-dimensional flow. J. Fluid Mech. 265–301.Google Scholar
Greenspan, H. P. 1969 The Thoery of Rotating Fluids. Cambridge University Press.Google Scholar
Haller, G. & Beron-Vera, F. J. 2012 Geodesic theory of transport barriers in two-dimensional flows. Physica D 241, 1680–1702 doi:10.1016/j.physd.2012.06.012.Google Scholar
Haller, G. & Poje, A. C. 1998 Finite time transport in aperiodic flows. Physica D 119, 352–380.CrossRefGoogle Scholar
Hart, J. E. & Kittelman, S. 1996 Instabilities of the sidewall boundary layer in a differentially driven rotating cylinder. Phys. Fluids 8, 692–696.Google Scholar
Haza, A. C., Griffa, A., Martin, P., Molcard, A., Özgökmen, T. M., Poje, A. C., Barbanti, R., Book, J. W., Poulain, P. M., Rixen, M. & Zanasca, P. 2007 Model-based directed drifter launches in the Adriatic Sea: results from the DART experiment. Geophys. Res. Lett. 34, L10605 doi:10.1029/2007GL029634.CrossRefGoogle Scholar
Haza, A., Özgökmen, T., Griffa, A., Molcard, A., Poulain, P. & Peggion, G. 2010 Transport properties in small scale coastal flows: relative dispersion from VHF radar measurements in the Gulf of La Spezia. Ocean Dyn. 60, 861–882.Google Scholar
Haza, A. C., Poje, A., Özgökmen, T. M. & Martin, P. 2008 Relative dispersion from a high- resolution coastal model of the Adriatic Sea. Ocean Model. 22, 48–65.Google Scholar
Ilicak, M., Özgökmen, T., Özsöy, E. & Fischer, P. 2009 Non-hydrostatic modelling of exchange flows across complex geometries. Ocean Model. 29, 159–175.CrossRefGoogle Scholar
Joseph, B. & Legras, B. 2002 Relation between kinematic boundaries, stirring, and barriers for the Antarctic Polar Vortex. J. Atmos. Sci. 59, 1198–1212.Google Scholar
Kruznetsov, L., Toner, M., Kirwan, A. D. Jr, Jones, C. K. R. T., Kantha, L. H. & Choi, J. 2002 The loop current and adjacent rings delineated by Lagrangian analysis of the near-surface flow. J. Mar. Res. 60, 405–429.Google Scholar
Lackey, T. C. & Sotiropoulos, F. 2006 Relationship between stirring rate and Reynolds number in the chaotically advected steady flow in a container with exactly counter-rotating lids. Phys. Fluids 18 (5), 053601.Google Scholar
Ledwell, J. R., McGillicuddy, D. J. & Anderson, L. A. 2008 Nutrient flux into an intense deep chlorophyll layer in a mode-water eddy. Deep-Sea Res. II 55, 1139–1160.Google Scholar
Lichtenberg, A. J. & Lieberman, M. A. 1992 Regular and Chaotic Dynamics. Springer.Google Scholar
Lipphardt, B. L. Jr, Poje, A. C., Kirwan, A. D. Jr, Kantha, L. & Zweng, M. 2008 Death of three loop current rings. J. Mar. Res. 66, 25–60.Google Scholar
Lipphardt, B. L. Jr, Small, D., Kirwan, A. D. Jr, Wiggins, S., Ide, K., Grosch, C. E. & Paduan, J. D. 2006 Synoptic Lagrangian maps: applications to surface transport in Monterey Bay. J. Mar. Res. 64, 221–247.Google Scholar
Lopez, J. M. 1998 Characteristics of endwall and sidewall boundary layers in a rotating cylinder with a differentially rotating endwall. J. Fluid Mech. 359, 49–79.CrossRefGoogle Scholar
Lopez, J. M. & Marques, F. 2010 Sidewall boundary layer instabilities in a rapidly rotating cylinder driven by a differentially co-rotating lid. Phys. Fluids 22, 114109.Google Scholar
Lozier, S. M., Pratt, L. J., Rogerson, A. R. & Miller, P. D. 1997 Exchange geometry revealed by float trajectories in the gulf stream. J. Phys. Oceanogr. 27, 2327–2341.Google Scholar
Maday, Y. & Patera, A. T. 1989 Spectral element methods for the Navier–Stokes equations. In State of the Art Surveys in Computational Mechanics (ed. Noor, A. K.), pp. 71–143. ASME.Google Scholar
Malhotra, N. & Wiggins, S. 1998 Geometric structues, lobe dynamics, and Lagrangian transport in flows with aperiodic time-dependence, with applications to Rossby wave flow. J. Nonlinear Sci. 8, 401–456.Google Scholar
Marshall, J. & Schott, F. 1999 Open-ocean convection: observations, theory and models. Rev. Geophys. 37, 1–64.Google Scholar
McGillicuddy, D. J., Anderson, L. A., Bates, N. R., Bibby, T., Buesseler, K. O., Carlson, C., Davis, C. S., Ewart, C., Falkowski, P. G., Goldthwait, S. A., Hansell, D. A., Jenkins, W. J., Johnson, R., Kosnyrev, V. K., Ledwell, J. R., Li, Q. P., Siegel, D. A. & Steinberg, D. K. 2007 Eddy/wind interactions stimulate extraordinary mid-ocean plankton blooms. Science 316 (5827), 1021–1026 doi:10.1126/science.1136256.Google Scholar
Mezic, I. 2001 Chaotic advection in bounded Navier–Stokes flows. J. Fluid Mech. 431, 347–370.Google Scholar
Mezic, I. & Wiggins, S. 1994 On the integrability of perturbations of three-dimensional fluid flows with symmetry. J. Nonlinear Sci. 4, 157–194.Google Scholar
Miller, P. D., Pratt, L. J., Helflrich, K. R. & Jones, C. K. R. T. 2002 Chaotic transport of mass and potential vorticity for an island circulation. J. Phys. Oceanogr. 32, 80–102.Google Scholar
Mullowney, P., Julian, K. & Meiss, J. D. 2005 Blinking rolls: chaotic advection in a 3D flow with an invariant. SIAM J. Appl. Dyn. Syst. 4, 159–186.Google Scholar
Mullowney, P., Julian, K. & Meiss, J. D. 2008 Chaotic advection and the emergence of tori in the Kuppers–Lortz state. Chaos 18, 033104.Google Scholar
Ngan, K. & Shephard, T. G. 1999 A closer look at chaotic advection in the stratosphere. Part I: geometric structure. J. Atmos. Sci. 56, 4134–4152.Google Scholar
Ottino, J. M. 1989 The Kinematics of Mixing: Stretching, Chaos, and Transport. Cambridge University Press.Google Scholar
Özgökmen, T. & Fischer, P. 2008 On the role of bottom roughness in overflows. Ocean Model. 20, 336–361.CrossRefGoogle Scholar
Özgökmen, T. & Fischer, P. 2012 CFD application to oceanic mixed layer sampling with Lagrangian platforms. Intl J. Comput. Fluid. Dyn. 26, 337–348.Google Scholar
Özgökmen, T. M., Fischer, P. F., Duan, J. & Iliescu, T. 2004a. Three-dimensional turbulent bottom density currents from a high-order nonhydrostatic spectral element model. J. Phys. Oceanogr. 34 (9), 2006–2026.Google Scholar
Özgökmen, T. M., Fischer, P. F., Duan, J. & Iliescu, T. 2004b. Entrainment in bottom gravity currents over complex topography from three-dimensional nonhydrostatic simulations. Geophys. Res. Lett. 31, L13212, doi:10.1029/2004GL020186.Google Scholar
Özgökmen, T., Fischer, P. & Johns, W. 2006 Product water mass formation by turbulent den- sity currents from a high-order nonhydrostatic spectral element model. Ocean Model. 12, 237–267.Google Scholar
Özgökmen, T., Iliescu, T. & Fischer, P. 2009a Large eddy simulation of stratified mixing in a three-dimensional lock-exchange system. Ocean Model. 26, 134–155.CrossRefGoogle Scholar
Özgökmen, T., Iliescu, T. & Fischer, P. 2009b Reynolds number dependence of mixing in a lock-exchange system from direct numerical and large eddy simulations. Ocean Model. 30, 190–206.Google Scholar
Özgökmen, T., Iliescu, T., Fischer, P., Srinivasan, A. & Duan, J. 2007 Large eddy simulation of stratified mixing in two-dimensional dam-break problem in a rectangular enclosed domain. Ocean Model. 16, 106–140.Google Scholar
Özgökmen, T., Poje, A., Fischer, P., Childs, H., Krishnan, H., Garth, C., Haza, A. & Ryan, E. 2012 On multi-scale dispersion under the influence of surface mixed layer instabilities and deep flows. Ocean Model. 56, 16–30.Google Scholar
Özgökmen, T., Poje, A., Fischer, P. & Haza, A. 2011 Large eddy simulations of mixed layer instabilities and sampling strategies. Ocean Model. 39, 311–331.CrossRefGoogle Scholar
Pattanayak, A. K. 2001 Characterizing the metastable balance between chaos and diffusion. Physica D 148, 1–19.Google Scholar
Patera, A. 1984 A spectral element method for fluid dynamics; laminar flow in a channel expansion. J. Comput. Phys. 54, 468–488.CrossRefGoogle Scholar
Pedlosky, T. & Spall, M. A. 2005 Boundary intensification of vertical velocity in a $\beta $ -plane basin. J. Phys. Oceanogr. 35, 2487–2500.Google Scholar
Poje, A. C. & Haller, G. 1999 Geometry of cross-stream mixing in a double-gyre ocean model. J. Phys. Oceanogr. 29, 1649–1665.Google Scholar
Poje, A., Haza, A., Ozgokmen, T., Magaldi, M. & Garraffo, Z. 2010 Resolution dependent relative dispersion statistics in a hierarchy of ocean models. Ocean Model. 31, 36–50.Google Scholar
Pratt, L. J., Lozier, M. S. & Beliakova, N. 1995 Parcel trajectories in quasigeostrophic jets: neutal modes. J. Phys. Oceanogr. 25, 1451–1466.Google Scholar
Rogerson, A. M., Miller, P., Pratt, L. J. & Jones, C. K. R. T. 1999 Lagrangian motion and fluid exchange in a barotropic meandering jet. J. Phys. Oceanogr. 29, 2635–2655.Google Scholar
Rypina, I. I., Brown, M. G., Beron-Vera, F. J., Kocak, H., Olascoaga, M. J. & Udovydchenkov, I. A. 2007a On the Lagrangian dynamics of atmospheric zonal jets and the permeability of the stratospheric polar vortex. J. Atmos. Sci. 64, 3593–3610.Google Scholar
Rypina, I. I., Brown, M. G., Beron-Vera, F. J., Kocak, H., Olascoaga, M. J. & Udovydchenkov, I. A. 2007b Robust transport barriers resulting from strong Kolmogorov–Arnold–Moser stability. Phys. Rev. Lett. 98, 104102. doi:10.1103/PhysRevLett.98.10410.Google Scholar
Rypina, I. I., Brown, M. G. & Kocak, H. 2009 Transport in an idealized three-gyre system with an application to the adriatic sea. J. Phys. Oceanogr. 39, 675–690.Google Scholar
Rypina, I. I., Pratt, L. J. & Lozier, S. M. 2011 Near-surface transport pathways in the North Atlantic Ocean. J. Phys. Oceanogr. 41, 911–925.Google Scholar
Rypina, I. I., Pratt, L. J., Pullen, J., Levin, J. & Gordon, A. 2010 Chaotic advection in an archipelago. J. Phys. Oceanogr. 40, 1988–2006.Google Scholar
Rypina, I. I., Scott, S., Pratt, L. J. & Brown, M. G. 2011 Investigating the connection between complexity of isolated trajectories and Lagrangian coherent structures. Nonlinear Proc. Geophys. 18, 977–987. doi:10.5194.Google Scholar
Samelson, R. M. 1992 Fluid exchange across a meandering jet. J. Phys. Oceanogr. 22, 431–440.Google Scholar
Samelson, R. M. & Wiggins, S. 2006 Lagrangian Transport in Geophysical Jets and Waves: The Dynamical Systems Approach. Springer.Google Scholar
Shadden, S. C., Lekien, F., Paduan, J. D., Chavez, F. P. & Marsden, J. E. 2009 Correlation between surface drifters and coherent structures from high-frequency radar data in Monterey Bay. Deep-Sea Res. II 56, 161–172.Google Scholar
Shott, F. M., Visbeck, M., Send, U., Fisher, J., Stramma, L. & Desaubies, Y. 1996 Observations of deep convection in the Gulf of Lions, Northern Mediterranean, during the winter of 1991/92. J. Phys. Oceanogr. 26, 505–524.Google Scholar
Solomon, T. H. & Mezic, I. 2003 Uniform resonant chaotic mixing in fluid flows. Nature 425, 376–380.CrossRefGoogle ScholarPubMed
Sommeria, J. S., Meyers, D. & Swinney, H. L. 1989 Laboratory models of a planetary eastward jet. Nature 337, 58–61.Google Scholar
Sundermeyer, M. A., Terray, E. A., Ledwell, J. R., Cunningham, A. G., LaRocque, P. E., Banic, J. & Lillycrop, W. J. 2007 Three-dimensional mapping of fluorescent dye using a scanning, depth-resolving airborne radar. J. Atmos. Ocean. Technol. 24, 1050–1065.CrossRefGoogle Scholar
Thomas, L. N. & Rhines, P. B. 2002 Nonlinear stratified spin up. J. Fluid Mech. 473, 211–244.Google Scholar
Yuan, G.-C., Pratt, L. J. & Jones, C. K. R. T. 2004 Cross-jet transport and mixing in a $2\hspace{0.167em} 1/ 2$ -layer model. J. Phys. Oceangr. 34, 1991–2005.Google Scholar
Zaslavsky, G. M. & Chirikov, B. V. 1972 Stochastic instability of non-linear oscillations. Sov. Phys. Uspekhi 14, 549–672.Google Scholar