Article contents
Centrifugal instability in non-axisymmetric vortices
Published online by Cambridge University Press: 13 March 2015
Abstract
We study the centrifugal instability of non-axisymmetric vortices in the presence of an axial flow (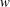 $w$) and a background rotation (
$w$) and a background rotation ( ${\it\Omega}_{z}$) using the local stability approach. Analytically solving the local stability equations for an axisymmetric vortex with
${\it\Omega}_{z}$) using the local stability approach. Analytically solving the local stability equations for an axisymmetric vortex with 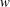 $w$ and
$w$ and 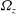 ${\it\Omega}_{z}$, growth rates for wave vectors that are periodic upon evolution around a closed streamline are calculated. The resulting sufficient criterion for centrifugal instability in an axisymmetric vortex is then heuristically extended to non-axisymmetric vortices and written in terms of integral quantities and their derivatives with respect to the streamfunction on a streamline. The new criterion for non-axisymmetric vortices, which converges to the exact criterion of Bayly (Phys. Fluids, vol. 31, 1988, pp. 56–64) in the absence of background rotation and axial flow, is validated by comparisons with numerically calculated growth rates for two different anticyclonic vortices: the Stuart vortex (specified by the concentration parameter
${\it\Omega}_{z}$, growth rates for wave vectors that are periodic upon evolution around a closed streamline are calculated. The resulting sufficient criterion for centrifugal instability in an axisymmetric vortex is then heuristically extended to non-axisymmetric vortices and written in terms of integral quantities and their derivatives with respect to the streamfunction on a streamline. The new criterion for non-axisymmetric vortices, which converges to the exact criterion of Bayly (Phys. Fluids, vol. 31, 1988, pp. 56–64) in the absence of background rotation and axial flow, is validated by comparisons with numerically calculated growth rates for two different anticyclonic vortices: the Stuart vortex (specified by the concentration parameter 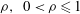 ${\it\rho},~0<{\it\rho}\leqslant 1$) and the Taylor–Green vortex (specified by the aspect ratio
${\it\rho},~0<{\it\rho}\leqslant 1$) and the Taylor–Green vortex (specified by the aspect ratio 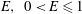 $E,~0<E\leqslant 1$). With no axial velocity and finite background rotation, the criterion predicts a lower and an upper threshold of
$E,~0<E\leqslant 1$). With no axial velocity and finite background rotation, the criterion predicts a lower and an upper threshold of 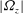 $|{\it\Omega}_{z}|$ between which centrifugal instability is present. We further demonstrate that the criterion represents an improvement over the criterion of Sipp & Jacquin (Phys. Fluids, vol. 12, 2000, pp. 1740–1748). Finally, in the presence of both axial velocity and background rotation, the criterion is shown to be accurate for large enough
$|{\it\Omega}_{z}|$ between which centrifugal instability is present. We further demonstrate that the criterion represents an improvement over the criterion of Sipp & Jacquin (Phys. Fluids, vol. 12, 2000, pp. 1740–1748). Finally, in the presence of both axial velocity and background rotation, the criterion is shown to be accurate for large enough 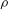 ${\it\rho}$ and
${\it\rho}$ and 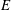 $E$.
$E$.
JFM classification
- Type
- Papers
- Information
- Copyright
- © 2015 Cambridge University Press
References
- 9
- Cited by



