Can isothermal plane Couette flow in fluid overlying porous layer be linearly unstable?

Abstract

The present study aims to examine the temporal linear stability analysis of isothermal plane Couette flow over a porous layer using the two-domain approach. The flow in the porous layer is described by the unsteady Darcy–Brinkman equations, whereas it is characterised by the Navier–Stokes equations in the fluid layer. In contrast to the Darcy model, it is observed that the isothermal plane Couette flow becomes unstable for such a superposed system on the inclusion of the Brinkman term. From the stability analysis, the two-dimensional mode is found to be least stable, and two modes of instability, namely porous mode and mixed mode are obtained under the consideration of the Darcy–Brinkman model along with advection term (DBA model). For Darcy number $(\delta )=0.01$, depending on the value of the stress-jump coefficient, mixed mode controls the instability of the system at small values of depth ratio $(\hat {d})$, and it disappears for relatively high values of $\hat {d}$, where the porous mode dominates. In addition, it has been observed that when $\hat {d}=0.1$, the critical mode of instability is found to be mixed for $\delta >0.02$ and porous for $\delta \le 0.02$. The stress-jump coefficient destabilises the flow in terms of energy production through perturbed stresses at the interface. As observed in the case of isothermal plane Poiseuille flow studied by Chang, Chen & Straughan (J. Fluid Mech., vol. 564, 2006, pp. 287–303), here also depth ratio (Darcy number) stabilises (destabilises) the flow. However, this characteristic does not remain valid when the advection term is eliminated from the considered momentum equation. For a certain range of $\hat {d} (\delta )$, the destabilising (stabilising) characteristic of the respective parameters are encountered when the fluid mode of instability prevails.

1. Introduction

Understanding and exploring the scenarios concerning the instability in one of Navier–Stokes (NS) equations’ simplest non-trivial solution, i.e. plane Couette flow, is long overdue amidst the fluid mechanics community. Rayleigh (1914) first suggested the stable nature of plane Couette flow to infinitesimal disturbances in a channel. The first scientific proof to the preceding fact was given by Davey (1973). He used a combination of asymptotic analysis and numerical computation to prove the same. Later on, Romanov (1973) showed that Couette flow in the channel is stable for all Reynolds numbers using the linear stability analysis. This result was further supported by Orszag & Patera (1980). However, Tillmark & Alfredsson (1992) executed the first flow visualisation for transition in plane Couette flow experimentally and determined the critical Reynolds number for turbulence as $360 \pm 10$ based on the half-height of the channel and half-velocity difference between the walls. Such contrasting results between theoretical and experimental studies led several researchers to look for possible instability in plane Couette flow in a channel. Furthermore, wherein the researchers were still finding the Couette flow to be linearly stable (Lee & Finlayson 1986), following Nield (2003), Shankar, Shivakumara & Kumar (2020) predicted the hydrodynamic instability of plane Couette flow in a channel filled with the porous medium by including the Brinkman as well as advection term in Darcy model.

The study of fluid flow through a channel in which the fluid layer overlies the porous layer has garnered considerable attention from the scientific world in the late 20th century in view of its immense applications in various geological and industrial frameworks. We quote a few notable results: water flow below the surface of the Earth (Ewings & Weekes 1998), the oil flow in subterranean reservoirs (Allen 1984) and the production of composite materials for the automobile and aircraft industries (Blest et al. 1999). In particular, the interplay between the injected fluid and the porous layers is very important in enhanced oil recovery techniques, such as gas injection and water flooding. Stability analysis in this context provides valuable insight into the flow dynamics, enabling engineers to determine the optimal injection rates and pressure. By analysing the stability of the flow, one can predict and address instabilities such as channelling or fingering, which can lead to inefficient displacement of oil. This ensures that the injected fluid displaces the oil uniformly and effectively, thereby maximising recovery efficiency. Furthermore, vessel dynamics in marine engineering requires a sound understanding of the Couette flow in fluid overlying porous layer to optimise the interaction between fluid flow and a vessel's structure (Gourlay 2006; Wang et al. 2018; Mukherjee & Giribabu 2021). This interaction can significantly affect performance, efficiency and safety by notably influencing drag through the water and the porous coating on a ship's hull. Along these lines, a theoretical understanding of Couette flow in fluid overlying porous layer will be beneficial and, consequently, in the present study, an attempt has been made in this direction.

As can be seen in literature, the isothermal plane Couette flow is linearly stable to infinitesimal disturbances under Darcy's law (Chang, Chen & Chang 2017). Even the inclusion of media anisotropy and inhomogeneity fails to render instability in this situation (Barman, Aleria & Bera 2024). In contrast to the linearly unstable nature of Newtonian fluid (Chang, Chen & Straughan 2006; Chang et al. 2017), the isothermal plane Poiseuille/Couette–Poiseuille flow in fluid overlying porous layer is linearly stable for a Bingham fluid (Sengupta & De 2019, 2020). However, using non-modal analysis, the instability characteristic of the flow has been analysed in such a superposed system. The instability in plane Couette flow in fluid overlying porous layer was first witnessed by Chang (2005), in which the author considered a constant temperature difference between the upper and lower plate, and recent developments in this direction are well-documented in the recent article of Barman et al. (2024). To the best of the authors’ knowledge, no literature exists that predicts the existence of instability in isothermal plane Couette flow through fluid overlying porous layer. Thus, the question that arises from the literature so far is whether it is possible to have a situation in which one can encounter the instability of isothermal plane Couette flow in the fluid overlying the porous layer. Answering this serves as the main objective of the present study.

The article advances as follows. Section 2 comprises the problem geometry and the governing equations, which is followed by exploring the neutral stability curves for possible existence of instability in § 3. It also reveals the physical cause behind the instability through the energy analysis and secondary flow patterns. The article ends with some concluding remarks in § 4.

2. Physical problem and mathematical formulation

2.1. Governing equations and boundary conditions

Consider a three-dimensional Couette flow in a horizontal fluid layer underlying a homogeneous and isotropic porous layer saturated with the same viscous, Newtonian and incompressible fluid (see figure 1). We assume that the physical properties of the fluid, namely, the density and dynamic viscosity, and the porous media properties, namely, the porosity and media permeability, are constant. Consider a Cartesian coordinate system $(x, y,z)$ with the origin at the fluid–porous interface, wherein $x$, $y$ and $z$ signify the streamwise, spanwise and cross-stream flow directions, respectively. The depth of the fluid and porous layers are $d$ and $d_m$, respectively. The upper plate of the fluid layer moves with a uniform velocity $U$ in the streamwise direction, and the occupying space of the flow is $\{(x, y, z) \in {\mathbb {R}}^2 \times (-d_m, d) \}$. A two-domain approach has been chosen to understand the role of location of the interface on the stability of the above shear-induced flow.

Figure 1. Diagram of the physical problem.

The flow in the fluid layer is governed by the continuity and the NS equations as follows:

(2.1)$$\begin{gather} \boldsymbol{\nabla} \boldsymbol{\cdot} \boldsymbol{u}=0, \end{gather}$$

(2.2)$$\begin{gather}\rho \left(\frac{\partial \boldsymbol{u}}{\partial t}+\boldsymbol{u}\boldsymbol{\cdot} \boldsymbol{\nabla u}\right)={-}\boldsymbol{\nabla }p+ \mu\nabla^2 \boldsymbol{u}, \end{gather}$$

where $\boldsymbol {u}=(u,v,w)$, $p$, $\rho$ and $\mu$ denote velocity vector, pressure, density and viscosity, respectively. The operator $\boldsymbol {\nabla }$ is defined as $\boldsymbol {\nabla } = ({\partial }/{(\partial x)},{\partial }/{(\partial y)},{\partial }/{(\partial z)})$.

Note that flow in a porous layer can also be governed by continuity and NS equations along with no-penetration and no-slip conditions at the fluid–solid interfaces. In general, a porous medium's structure is either a sponge-like porous foam (e.g. metal-foam) or porous bed of packed particles (e.g. sand, gravel and aloxite). In the porous layer, several length scales are present: (i) average pore diameter ($l_f$); (ii) average particle diameter ($l_s$); and (iii) thickness of the porous layer ($d_m$). The first two are on a small scale, whereas the last is on a large scale. Due to the different length scales and complex boundary conditions, solving the boundary value problem governed by continuity and NS equations becomes very difficult. In this situation, the volume averaging method simplifies the issue by considering only the large-scale behaviour of the flow in the porous region (Tilton & Cortelezzi 2008). There are two types of volume averages: the superficial and intrinsic averages used in the volume averaging method. For a field variable $\phi _f$ in the fluid phase, the superficial and intrinsic averages are defined as

(2.3)\begin{equation} \langle \phi_f \rangle = \frac{1}{V}\int_{V_f} \phi_f \,{\rm d}V_f, \end{equation}

and

(2.4)\begin{equation} \langle \phi_f \rangle ^f = \frac{1}{V_f}\int_{V_f} \phi_f \,{\rm d}V_f, \end{equation}

respectively, and they are related by $\langle \phi _f \rangle = \chi \langle \phi _f \rangle ^f$, where $\chi$ is the porosity. Here, $V_f < V$ is the volume of fluid contained in the averaging volume, $V$ and ${V_f}/{V} = \chi$. Following the convention of Whitaker (1996), i.e. for an incompressible viscous flow, the velocity vector has to satisfy solenoidal characteristics but not pressure, one can derive the following continuity and volume-averaged NS equations:

(2.5)\begin{equation} \boldsymbol{\nabla} \boldsymbol{\cdot} \langle{\boldsymbol{u}}\rangle=0, \end{equation}

(2.6)\begin{align} &\rho \left [{\frac{1}{\chi }\frac{\partial\langle{\boldsymbol{u}}\rangle}{\partial t}+\frac{1}{\chi ^{2}}\langle{\boldsymbol{u}}\rangle\boldsymbol{\cdot}\boldsymbol{\nabla}\langle{\boldsymbol{u}}\rangle+\frac{c_F}{K^{1/2}} | \langle{\boldsymbol{u}}\rangle | \langle{\boldsymbol{u}}\rangle} +\boldsymbol{\nabla}\boldsymbol{\cdot}\langle \hat{\boldsymbol{u}}\,\hat{\boldsymbol{u}} \rangle \right]\nonumber\\ &\quad ={-}\boldsymbol{\nabla} \langle p \rangle^f+{\mu}\nabla^2 \langle{\boldsymbol{u}}\rangle-\frac{\mu}{K}{\langle{\boldsymbol{u}}\rangle}, \end{align}

where ${\langle {\boldsymbol {u}}\rangle }$ is the superficial volume-averaged velocity, which is also called the Darcy velocity, $\langle p \rangle ^f$ is the intrinsic volume-averaged pressure, $c_F$ is the form drag coefficient and $K$ is the permeability of the porous medium. In this equation, the Darcy term $(\mu \langle {\boldsymbol {u}}\rangle /K)$ represents a volume-averaged viscous drag, the Brinkman term $(\mu \nabla ^2 \langle {\boldsymbol {u}}\rangle )$ represents a volume-averaged viscous diffusion, the Forchheimer term ($\rho c_FK^{-1/2}|\langle {\boldsymbol {u}}\rangle |\langle {\boldsymbol {u}}\rangle$) represents form-drag due to inertial effects and the advection term $(\rho \langle {\boldsymbol {u}}\rangle \boldsymbol {\cdot }\boldsymbol {\nabla }\langle {\boldsymbol {u}}\rangle /\chi ^{2})$ represents another drag that arises from inertial effects.

It is important to mention that when the difference between the velocity of the fluid and the volume-averaged velocity of the fluid $( \langle \hat {\boldsymbol {u}} \rangle )$ is negligible, the advection term in the NS equation generates the terms ${\rho \langle {\boldsymbol {u}}\rangle \boldsymbol {\cdot }\boldsymbol {\nabla }\langle {\boldsymbol {u}}\rangle }/{\chi ^{2}}$ and $\rho c_FK^{-1/2}|\langle {\boldsymbol {u}}\rangle |\langle {\boldsymbol {u}}\rangle$ that are of order of ${{O}}(\rho |\langle {\boldsymbol {u}}\rangle |^2/{\chi ^{2}d_m})$ and ${{O}}(\rho c_F |\langle {\boldsymbol {u}}\rangle |^2/{l_f})$, respectively. This indicates that the contribution of advection term ${\rho \langle {\boldsymbol {u}}\rangle \boldsymbol {\cdot }\boldsymbol {\nabla }\langle {\boldsymbol {u}}\rangle }/{\chi ^{2}}$ is negligible in comparison with the dominant Forchheimer term, $\rho c_FK^{-1/2}|\langle {\boldsymbol {u}}\rangle |\langle {\boldsymbol {u}}\rangle$. Note that the appropriate value of $c_F$ for a given porous medium depends on experimental data. Due to insufficient experimental data, in practice, the inertia effects via form drag are generally dropped (Hill & Straughan 2009; Lasseux, Valdés-Parada & Bellet 2019). Furthermore, without a advection term, there is no mechanism for developing the flow field, which leads to a physically flawed and unrealistic situation (Vafai & Kim 1995). The present study concerns the flow through porous materials whose permeability is relatively low, so the inertial effect is expected to be low. Accordingly, the flow in porous medium is modelled by the Darcy–Brinkman equation along with time derivative $(({\rho }/{\chi })({\partial \langle {\boldsymbol {u}}\rangle }/{\partial t}))$ and advection term ($\rho {\langle {\boldsymbol {u}}\rangle \boldsymbol {\cdot }\boldsymbol {\nabla }\langle {\boldsymbol {u}}\rangle }/{\chi ^{2}}$). This model will be referred to as the DBA model from here onwards.

Furthermore, representing spatial volume-averaged velocity, $\langle {\boldsymbol {u}}\rangle$, and intrinsic volume-averaged pressure, $\langle p \rangle ^f$, as $\boldsymbol {u}_{\boldsymbol {m}}$ and $p_m$, respectively, the governing equations in porous layer are transformed as follows:

(2.7)$$\begin{gather} \boldsymbol{\nabla}\boldsymbol{\cdot} \boldsymbol{u}_{\boldsymbol{m}}=0, \end{gather}$$

(2.8)$$\begin{gather}\frac{\rho}{\chi}\frac{\partial \boldsymbol{u}_{\boldsymbol{m}}}{\partial t} + \dfrac{\rho}{\chi^{2}} \boldsymbol{u}_{\boldsymbol{m}}\boldsymbol{\cdot}\boldsymbol{\nabla}\boldsymbol{u}_{\boldsymbol{m}} ={-}\boldsymbol{\nabla}p_m-\frac{\mu}{K}\boldsymbol{u}_{\boldsymbol{m}}+\frac{\mu}{\chi}\nabla^2 \boldsymbol{u}_{\boldsymbol{m}}, \end{gather}$$

where $\boldsymbol {u}_{\boldsymbol {m}} = (u_m, v_m, w_m)$.

The dimensional no-slip and no-penetration conditions are considered at the upper and lower layers of the system, which are as follows:

(2.9)$$\begin{gather} u=U,\quad v=w=0\quad \text{at } z=d, \end{gather}$$

(2.10)$$\begin{gather}\boldsymbol{u}_{\boldsymbol{m}}=0 \quad \text{at } z={-}d_m. \end{gather}$$

With respect to interface conditions, we assume the continuity conditions, i.e. continuity of velocity,

(2.11)\begin{equation} \boldsymbol{u}=\boldsymbol{u}_{\boldsymbol{m}} \end{equation}

and normal stresses,

(2.12)\begin{equation} p-2\mu\dfrac{\partial w}{\partial z}=p_m-\left(\dfrac{2\mu}{\chi}\right)\dfrac{\partial w_m}{\partial z}. \end{equation}

The continuity of velocity at the interface ensures mass conservation, preventing any unrealistic accumulation or depletion of mass. In addition, the forces exerted by the fluid and the porous medium on each other must be balanced. Further conditions related to tangential stresses must also be considered, which are given by the following equations:

(2.13a,b)\begin{equation} \frac{\partial u}{\partial z}= \frac{1}{\chi}\frac{\partial u_m}{\partial z}-\frac{\beta}{\sqrt{K}}u_m,\quad \frac{\partial v}{\partial z}= \frac{1}{\chi}\frac{\partial v_m}{\partial z}-\frac{\beta}{\sqrt{K}}v_m, \end{equation}

where $\beta$ is the stress-jump coefficient Ochoa-Tapia & Whitaker (1995a). However, Hill & Straughan (2009) have utilised the generalisation of the condition of Jones (1973)

(2.14)$$\begin{gather} \frac{\partial u}{\partial z} + \frac{\partial w}{\partial x} = \frac{1}{\chi}\left( \frac{\partial u_m}{\partial z} + \frac{\partial w_m}{\partial x}\right) -\frac{\beta}{\sqrt{K}}u, \end{gather}$$

(2.15)$$\begin{gather}\frac{\partial v}{\partial z} + \frac{\partial w}{\partial y} = \frac{1}{\chi}\left( \frac{\partial v_m}{\partial z} + \frac{\partial w_m}{\partial y}\right) -\frac{\beta}{\sqrt{K}}v, \end{gather}$$

to include the shear stress at the interface, but in this study, we use the approach of Ochoa-Tapia & Whitaker (1995a), as it has shown better agreement with experimental observations. Furthermore, we have compared the effects of these two different interface conditions on the instability point and found that the results between the two remain largely consistent (table 7). A thorough and detailed discussion on the interface condition can be found in the work of Ochoa-Tapia & Whitaker (1995a,b).

To proceed with the linear stability analysis of the plane Couette flow, we non-dimensionalise the above governing equations (2.1)–(2.2) for fluid layer, (2.7)–(2.8) for porous layer, boundary conditions (2.9)–(2.10) and interface conditions (2.11)–(2.14). For the same, in the fluid layer, the lengths are non-dimensionalised by $d$, velocity components by $U$, time by $d/U$ and pressure by $\mu U/d$. Thus, the non-dimensional governing equations for the fluid layer become

(2.16)$$\begin{gather} \boldsymbol{\nabla} \boldsymbol{\cdot} \boldsymbol{u}=0, \end{gather}$$

(2.17)$$\begin{gather}Re\left(\frac{\partial \boldsymbol{u}}{\partial t}+\boldsymbol{u}\boldsymbol{\cdot} \boldsymbol{\nabla u}\right)={-}\boldsymbol{\nabla}p+\nabla^2 \boldsymbol{u}. \end{gather}$$

Here, $Re = Ud/\nu$ is the Reynolds number, where $\nu$ represents the kinematic viscosity of the fluid.

For the porous layer, lengths are non-dimensionalised by $d_m$, velocity components by $U_m$, where $U_m$ is the basic velocity component along the horizontal direction in the porous layer at $z_m=0$, time by $d_m/U_m$ and pressure by $\mu U_m/d_m$. Hence, the non-dimensional governing mass and momentum equations for the porous layer are

(2.18)$$\begin{gather} \boldsymbol{\nabla}_{\boldsymbol{m}} \boldsymbol{\cdot} \boldsymbol{u}_{\boldsymbol{m}}=0, \end{gather}$$

(2.19)$$\begin{gather}\frac{Re_m}{\chi}\left(\frac{\partial \boldsymbol{u}_{\boldsymbol{m}}}{\partial t_m}+\dfrac{1}{\chi}\boldsymbol{u}_{\boldsymbol{m}} \boldsymbol{\cdot} \boldsymbol{\nabla}_{\boldsymbol{m}} \boldsymbol{u}_{\boldsymbol{m}}\right)={-}\boldsymbol{\nabla}_{\boldsymbol{m}}p_m- \frac{1}{\delta^2}\boldsymbol{u}_{\boldsymbol{m}}+\frac{1}{\chi}\nabla_m^2 \boldsymbol{u}_{\boldsymbol{m}}, \end{gather}$$

where $\nabla _m$ is defined as $\nabla _m = ({\partial }/{(\partial x_m)},{\partial }/{(\partial y_m)}, {\partial }/{(\partial z_m)})$. In the above equations, $\delta =\sqrt {K}/d_m$ is the Darcy number. The Reynolds number in the porous layer is defined as $Re_m=U_m d_m/\nu$.

The non-dimensional boundary conditions are as follows:

(2.20)$$\begin{gather} u=1,\quad v=w=0\quad \text{at } z=1 , \end{gather}$$

(2.21)$$\begin{gather}\boldsymbol{u}_{\boldsymbol{m}}=0 \quad \text{at } z_m={-}1. \end{gather}$$

At the interface of fluid and porous layers, i.e. at $z=0=z_m$:

(2.22)$$\begin{gather} Re\,\boldsymbol{u}=Re_m \hat{d}\boldsymbol{u}_{\boldsymbol{m}},\quad p-2\frac{\partial w}{\partial z}=\left(\frac{\hat{d}^2Re_m}{Re}\right)p_m-\left(\frac{2\hat{d}^2}{\chi}\right) \left(\frac{Re_m}{Re}\right)\frac{\partial w_m}{\partial z_m}, \end{gather}$$

(2.23)$$\begin{gather}\left(\frac{Re}{\hat{d}^2 Re_m}\right)\frac{\partial u}{\partial z}= \frac{1}{\chi}\frac{\partial u_m}{\partial z_m}-\frac{\beta}{\delta}u_m,\quad \left(\frac{Re}{\hat{d}^2 Re_m}\right)\frac{\partial v}{\partial z}= \frac{1}{\chi}\frac{\partial v_m}{\partial z_m}-\frac{\beta}{\delta}v_m, \end{gather}$$

where $\hat {d}=d/d_m$ is the depth ratio.

2.2. Basic state

We are interested in studying the linear stability analysis of the base flow to infinitesimal disturbances. For this, we assume that the flow is steady, unidirectional and fully developed. The non-dimensional base flow in the fluid and porous layers is given by

(2.24)\begin{align} \bar{U}&=\frac{\hat{d}(1+{\rm e}^{2\sqrt{\chi}/\delta})+\beta \sqrt{\chi} \hat{d}(1-{\rm e}^{2\sqrt{\chi}/\delta}) }{\hat{d}(1+{\rm e}^{2\sqrt{\chi}/\delta})-\delta\sqrt{\chi}(1-{\rm e}^{2\sqrt{\chi}/\delta})+\beta \sqrt{\chi} \hat{d}(1-{\rm e}^{2\sqrt{\chi}/\delta})}z\nonumber\\ &\quad-\frac{\delta \sqrt{\chi}(1-{\rm e}^{2\sqrt{\chi}/\delta})}{{\hat{d}(1+{\rm e}^{2\sqrt{\chi}/\delta}) -\delta\sqrt{\chi}(1-{\rm e}^{2\sqrt{\chi}/\delta})}+\beta \sqrt{\chi} \hat{d}(1-{\rm e}^{2\sqrt{\chi}/\delta})}, \end{align}

(2.25)\begin{equation} \bar{V}=\bar{W}=0, \end{equation}

and

(2.26)\begin{equation} \bar{U}_m={-}\frac{{\rm e}^{2\sqrt{\chi}/\delta}}{(1-{\rm e}^{2\sqrt{\chi}/\delta})}\,{\rm e}^{(\sqrt{\chi}/\delta )z_m}+\frac{1}{(1-{\rm e}^{2\sqrt{\chi}/\delta})}\,{\rm e}^{-(\sqrt{\chi}/\delta )z_m},\quad \bar{V}_m=\bar{W}_m=0, \end{equation}

respectively.

As can be seen from (2.24), the fluid velocity is linear in nature. In contrast to a Darcy porous layer (Chang et al. 2017), (2.26) gives the non-zero basic velocity, and the profile for the same is concave downwards. This might be the potential behind the instability of the plane Couette flow in the Darcy–Brinkman layer.

2.3. Perturbed state

The temporal linear stability analysis of the above base flow is performed by decomposing the flow variables into the base flow and infinitesimal perturbation as $q = \bar {Q} + q'$, where $\bar {Q}$ and $q'$ stand for the basic quantities and the perturbation quantities, respectively. The perturbed variables are considered in normal mode form as

(2.27)$$\begin{gather} q'=Q(z)\exp({\rm i}ax+{\rm i}by-{\rm i}\sigma t), \end{gather}$$

(2.28)$$\begin{gather}q'_m=Q_m(z_m)\exp({\rm i}a_mx_m+{\rm i}b_my-{\rm i}\sigma_m t_m ), \end{gather}$$

for both fluid and porous layers, respectively, with the relation $a=\hat {d}a_m$, $b=\hat {d}b_m$ and $\sigma =({Re_m\hat {d}^2}/{Re})\sigma _m$. Here, $a$ and $b$ are wavenumbers in $x$ and $y$ directions in the fluid layer, respectively, and $a_m$ and $b_m$ are the corresponding wavenumbers in the porous layer. In the present article, we have focused on the temporal linear stability analysis where wavenumbers are real, and wave speeds $\sigma =\sigma ^r+{\rm i}\sigma ^i$ and $\sigma _m=\sigma _m^r+{\rm i}\sigma _m^i$ are complex (Sengupta & De 2021; Zou et al. 2023). Depending on whether $\sigma ^i< 0$, $\sigma ^i= 0$, or $\sigma ^i > 0,$ the perturbations are categorised as stable, neutrally stable or unstable, respectively. Since it is observed that two-dimensional disturbances are least stable (see table 6 in Appendix A), it is sufficient to study the stability analysis of isothermal plane Couette flow by considering two-dimensional disturbances. Consequently, the spanwise components of wavenumber $b$ and $b_m$ are considered as zero.

After substituting (2.27)–(2.28) in (2.16)–(2.25) and neglecting the nonlinear terms in the resulting equations, the perturbed governing equations and boundary conditions are as follows:

(2.29)\begin{equation} (D^2-a^2-{\rm i}a \,Re\,\bar{U})(D^2-a^2)W ={-}{\rm i}\sigma \,Re (D^2-a^2)W, \end{equation}

(2.30)\begin{align} &\left(\frac{D_m^2-a_m^2}{\chi} -\frac{1}{\delta^2}\right)(D_m^2-a_m^2)W_m-\frac{{\rm i}a_m Re_m}{\chi^2}(D_m^2-a_m^2-D_m^2\bar{U}_m)W_m\nonumber\\ &\quad={-}\frac{{\rm i}\sigma_mRe_m}{\chi}(D_m^2-a_m^2)W_m, \end{align}

(2.31)$$\begin{gather} W(1)=DW(1)=0, \end{gather}$$

(2.32)$$\begin{gather}W_m({-}1)=D_mW_m({-}1)=0, \end{gather}$$

(2.33a,b)$$\begin{gather}Re\,W(0) = Re_m\hat{d} W_m(0), \quad Re\,DW(0)=Re_m \hat{d}^2D_mW_m(0), \end{gather}$$

(2.34)\begin{align} & D^3W(0)-{\rm i} a\, Re \,\bar{U}(0)DW(0)+{\rm i} a\,Re\,D\bar{U}(0)W(0)-3a^2DW+\left(\frac{\hat{d}^4 Re_m}{Re\,\delta^2}\right)D_m W_m(0)\nonumber\\ &\quad -\left(\frac{\hat{d}^4 Re_m}{\chi \,Re}\right)D_m^3W_m(0)+\left(\frac{Re_m \hat{d}^4}{\chi \,Re}\right)a_m^2D_m W_m(0)-\left(\frac{\hat{d}^4Re_m^2}{\chi^2 \,Re}\right){\rm i} a_m\bar{U}_mD_m W_m\nonumber\\ &\quad+\left(\frac{\hat{d}^4Re_m^2}{\chi^2 Re}\right) {\rm i} a_m D_m\bar{U}_m W_m ={-}{\rm i}\sigma \,Re \,DW(0)+{\rm i}\sigma_m\left(\frac{\hat{d}^4 Re_m^2}{\chi \,Re}\right)D_m W_m(0), \end{align}

(2.35)\begin{equation} \frac{Re}{\hat{d}^3}D^2W(0)=\frac{Re_m}{\chi}D^2_mW_m(0)-\frac{\beta}{\delta}Re_m D_mW_m(0), \end{equation}

where $D={{\rm d}}/{{\rm d}z}$ and $D_m= {{\rm d}}/{{\rm d}z_m}$.

2.4. Kinetic energy budget

An immediate way to check whether the given flow can be unstable or not under linear theory is by looking at the sign of the rate of change of the disturbance kinetic energy (i.e. the sign of growth rate of kinetic energy). For the flow to be unstable, the rate of disturbance kinetic energy $(\delta _{KE})$ of the system must change its sign from negative to positive. Thus, to check the instability of the isothermal plane Couette flow as well as the mechanism of instability, the help of the energy budget analysis is taken.

The kinetic energy balance equations are obtained by multiplying the disturbed velocity vector to both sides of the linear disturbance momentum equations and then integrating the equations over $([0,1] \times [0,2{\rm \pi} /a])$ for fluid layer and $([-1,0] \times [0,2{\rm \pi} /a_m])$ for porous layer (Boomkamp & Miesen 1996; Sharma, Aleria & Bera 2024). Combining the equations for fluid and porous layers, the kinetic energy balance equation takes the standard form:

(2.36)\begin{equation} \delta_{KE}=\dfrac{\partial(KE)}{\partial t}+\dfrac{\partial(KE_m)}{\partial t_m}=E_s+E_d+E_I+E_{d_m}+E_{D_m}. \end{equation}

In (2.36), the transfer of kinetic energy via Reynolds stress from or to the basic flow is represented by $E_s$, and energy dissipation via viscosity effects is represented by $E_d$ and $E_{d_m}$ for fluid and porous layer, respectively. The energy loss against surface drag is denoted by $E_{D_m}$. The disturbance kinetic energy due to work done by the perturbed stresses at the interface between the porous and fluid layers is represented by $E_I$. Here $KE$ and $KE_m$ denote the perturbed kinetic energy in the fluid and the porous layers, respectively. The expressions of each term in (2.36) are given in Appendix B. The Gauss–Chebyshev quadrature formula is used to compute the integrals in (2.36). The instability mechanism of the flow and the type of mode are determined by the kinetic energy balance equation. The contribution of $E_d$, $E_{d_m}$ and $E_{D_m}$ in the kinetic energy budget is used in this study to define the type of mode. If the contribution of $E_d~(E_{d_m}+E_{D_m})$ is greater than $70\,\%$ in balancing the contribution of $E_s$, the instability is said to be dominated by fluid (porous) mode.

3. Numerical results and discussion

The Chebyshev spectral collocation method is used to solve the governing equations (2.29)–(2.30) and boundary conditions (2.31)–(2.35). Since, the Chebyshev polynomials are defined in $[-1, 1]$, the fluid layer $[0, 1]$ and porous layer $[-1,0]$ are transformed into $[-1, 1]$ by using the transformation $\eta =2z-1$ and $\eta _m=-2z_m-1$, respectively (Canuto et al. 1988; Anjali, Khan & Bera 2022). Thus, (2.29)–(2.30) together with boundary conditions (2.31)–(2.35) results in a generalised eigenvalue problem.

The flow is controlled by four parameters: depth ratio $(\hat {d})$, porosity $(\chi )$, Darcy number $(\delta )$ and stress-jump coefficient $(\beta )$. In general, the porosity value for natural porous media is $< 0.6$, where the Darcy model is normally used. However, for man-made porous media (e.g. metallic foam), the same may be close to 1, in which the non-Darcy model is preferred. A compilation of the porosity of some common porous materials is also given in table 1, in which the Darcy number $(\delta _p)$ is defined based on the pore size. In the present study, the Darcy number $(\delta )$ is defined based on the depth of the porous layer. The porous layer in our study primarily consists of either foametal A or foametal B. As mentioned in table 1, the Darcy number based on pore diameter $(\delta _p)$ for foametal A is $2.42\times 10^{-1}$, where porous diameter is $4.06\times 10^{-4}$ m. Darcy number based on the depth of the porous layer $(\delta )$ can be given as $\delta =\delta _p\times {d_p}/{d_m}$. For example, when the thickness of the porous layer is 2.5 cm, $\delta$ will be approximately 0.004, whereas when the thickness is 1 cm, $\delta$ will be around 0.01. In the case of foametal B with a porous layer thickness of 1 cm, $\delta$ is estimated to be about 0.02. Similarly, for aluminum foam with a porous layer thickness of 0.5 cm, the value of $\delta$ will be approximately 0.1. Accordingly, $\delta$ is taken in the range $0.005\le \delta \le 0.1$ and $\chi$ is fixed at $0.78$ for most of the analysis. The selection of the range of the depth ratio is based on the fact that for $0.005\le \delta \le 0.01$, the maximum value of $\hat {d}$ for which the flow will be linearly unstable is found to be around 0.2, in fact for ${\delta }/{\hat {d}} < {10^{-1}}/{2}$ the flow is linearly stable. To cover most of the range of $\delta$, the upper limit of $\hat {d}$ is fixed at 0.2. On the other hand, decreasing $\hat {d}$ beyond 0.01, the flow characteristics remain almost the same on any further decrement of $\hat {d}$. Thus, the lower limit of $\hat {d}$ is fixed at 0.01. Therefore, to understand the role of the location of interface on the stability of flow $\hat {d}$ has been considered in the range $0.01\le \hat {d}\le 0.2$. The effect of stress-jump coefficient on the same is emphasised by taking two different values of $0$ and $0.7$ of $\beta$ (Ochoa-Tapia & Whitaker 1995b; Hill & Straughan 2009).

Table 1. Geometrical characteristics of some porous materials (Paek et al. 2000; Goyeau et al. 2003; Kamath, Balaji & Venkateshan 2011).

Before discussing the stability of the considered flow, the numerical code is verified in three different stages: first, the independence of solution on the order of polynomial; second, the comparison with existing results; and, third, whether the total rate of change of kinetic energy at the critical point is zero or not. The convergence of the numerical method is examined by varying the degree of Chebyshev polynomial, $N$, and is shown in table 2. It can be seen that $N = 70$ is sufficient to perform the numerical calculations. It is well known that plane Couette flow in a purely fluid channel is linearly stable (Romanov 1973; Orszag & Patera 1980). The similar characteristic is also observed for the present problem when the value of depth ratio is large (see table 3). For verifying our results with those of Chang et al. (2017), Darcy's law is chosen to model the porous media instead of the present model, and the Beavers–Joseph condition is used at the fluid–porous interface. The comparison between present and existing results for $\chi =0.3$, $\delta =0.001$, $\alpha =0.1$ (Beavers–Joseph constant) and $a=1.0$ are listed in table 4 and a good agreement between the results is found. Finally, it has been checked that the total rate of change of kinetic energy at the critical point is zero (shown in the subsequent result section). All the above analyses support the verification of the present numerical code. To check the possible existence of instability of the present problem, we have investigated whether the $\delta _{KE}$ will change its sign from negative to positive or not as a function of Reynolds number. It can be seen from figure 2 that the $\delta _{KE}$ changes its sign from negative to positive for $Re\in (100,800)$, thus indicating that isothermal plane Couette flow in a superposed fluid–porous system will be unstable under the consideration of present model.

Table 2. Convergence of the least-stable eigenvalue by Chebyshev spectral collocation method for $a=2$, $Re=500$, $\hat {d}=0.12$, $\chi =0.78$, $\delta =0.009$ and $\beta =0$.

Table 3. Eigenvalues with largest imaginary part for different values of $\hat {d}$ at $a=0.5$, $\chi =0.78$, $\delta =0.1$ and $\beta =0$.

Table 4. The largest imaginary parts of the leading eigenvalues obtained by Chang et al. (2017) and present study for different values of $\hat {d}$ and $Re$ at $\chi =0.3$, $\delta =0.001$, $\alpha =0.1$ and $a=1.0$.

Figure 2. Growth rate of kinetic energy as a function of $Re$ for $a=0.5$, $\hat {d}=0.1$, $\delta =0.01$ and $\chi =0.78$.

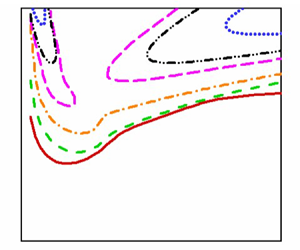
Figure 3(a,b) shows the neutral stability curve for different values of depth ratio at $\beta =0$ and $\beta =0.7$, respectively, wherein the neutral curve has either a single or dual lobe. From figure 3(a), for small values of depth ratio in the range $(0.01\le \hat {d}\le 0.05)$, the neutral curve has a single lobe. As $\hat {d}$ increases to $0.1$, two lobes of the neutral stability curve appear and $Re_c$ is observed in the left lobe. Whereas for $\hat {d}=0.2$, $Re_c$ shifts to the right lobe of the neutral stability curve. In the case of $\beta =0.7$, single lobe of the neutral curve is obtained for all considered values of $\hat {d}$. Here, for increasing the value of the stress jump coefficient, $Re_c$ decreases, which implies that the stress jump at the fluid–porous interface destabilises the flow. For both values of $\beta$, $Re_c$ increases on increasing the depth of the fluid layer, i.e. $\hat {d}$ stabilises the flow.

Figure 3. Neutral stability curves in $(a,Re)$ plane for different values of $\hat {d}$ at $\delta =0.01$ and $\chi =0.78$: (a) $\beta =0$; (b) $\beta =0.7$.

The value of different terms of the kinetic energy balance equation as a function of $\hat {d}$, at the critical point obtained from figure 3, are plotted in figure 4(a,b) for $\beta =0$ and $0.7$, respectively. It can be seen from figure 4(a), that the positive-definite term $E_s$ is mainly balanced by $E_{D_m}$ for $\hat {d}\ge 0.05$, whereas, for $\hat {d}<0.05$, $E_s$ is balanced by $E_d$, $E_{d_m}$ and $E_{D_m}$. Along these lines, the mode of instability is defined as porous for $\hat {d}\ge 0.05$, and mixed for $\hat {d}<0.05$. Similar characteristics can also be seen in figure 4(b). In this case, porous and mixed mode dominate the instability for $\hat {d}\ge 0.04$ and for $\hat {d}<0.04$, respectively. It is important to mention here that in contrast to $\beta =0$, here, the instability of flow is due to the combined effect of $E_s$ and $E_I$. The destabilising nature of $\beta$ in figure 3(b) is a consequence of the sizable contribution of $E_I$. Furthermore, a close look at figure 4(a) discloses that there exists a threshold value of $\hat {d}(\approx 0.165)$, beyond which the contribution of $E_{D_m}$ suddenly decreases and corresponding $E_{d_m}$ increases, which causes the shifting of $Re_c$ from left to right lobe in figure 3(a).

Figure 4. Different terms of kinetic energy balance as a function of $\hat {d}$ at $(a_c,Re_c)$ for $\delta =0.01$ and $\chi =0.78$: (a) $\beta =0$; (b) $\beta =0.7$.

As can be seen in the literature (Chang et al. 2017; Samanta 2020), the neutral curve displays a bimodal form and then a unimodal form as the depth ratio increases where the left lobe corresponds to the porous mode and the right lobe corresponds to the fluid mode. In the present study, two lobes for $\hat {d}\ge 0.1$ are obtained, and both lobes correspond to porous mode only. Here, the porous mode also becomes more stable for increasing values of $\hat {d}$.

The pattern of streamfunction at the critical states for $\hat {d}={0.02}$ and $0.1$, obtained from figure 3(a), are shown in figure 5(a,b), respectively, which allows for a deeper examination of the primary instability mode and aids in visualising the flow dynamics. The fluid layer extension from 0 to 1 and the porous layer extension from $-$1 to 0 are represented by the vertical axis. The critical wavelength, which is scaled by $\hat {d}$ for the porous layer, is depicted on the horizontal axis. As we can see, streamfunction patterns occupy both layers, however for $\hat {d}=0.1$, the penetration in porous layer is more in comparison with the same for $\hat {d}=0.02$, thus representing the porous and mixed mode, respectively. These findings support the results obtained from the energy budget analysis.

Figure 5. The streamfunction pattern at $\delta =0.01$, $\chi =0.78$ and $\beta =0$: (a) $(a_c,Re_c)=(0.651,140.913)$, $\hat {d}=0.02$; (b) $(a_c,Re_c)=(0.551,556.605)$, $\hat {d}=0.1$.

In order to understand the role of media permeability on the instability mechanism, the neutral stability curve in the $(a, Re)$-plane for different values of Darcy number and the corresponding energy budget spectrum at critical points are displayed in figure 6(a,b), respectively. It is observed that at $\delta =0.005$, the neutral stability curve has two lobes, both correspond to porous mode, and the critical value is obtained at $( 2.741,4634.666)$. The characteristic of the neutral stability curve remains the same for $\delta =0.008$ and $0.01$, but $Re_c$ decreases to 1794.759 and 556.605, respectively. On further increasing the value of $\delta$, the neutral stability curve with a single lobe is observed. Similar to figure 4, figure 6(b) also displays porous and mixed mode for $\delta \le 0.02$ and $\delta > 0.02$, respectively. In addition, also similar to figure 4, a jump in $E_{d_m}$ and $E_{D_m}$ can be seen at $\delta \approx 0.007$, which causes the shift in $Re_c$ from right to left lobe of neutral stability curve in figure 6(a). As mentioned in Chang et al. (2006), wherein the Darcy model is considered, an increase in $\delta$ causes the system to become more unstable. In the present study, the similar characteristic is observed for the considered range of $\delta$.

Figure 6. (a) Neutral stability curves for different values of $\delta$ and (b) energy components as a function of $\delta$ at $\hat {d}=0.1$, $\chi =0.78$ and $\beta =0$.

Now, we are curious to know whether the instability of Couette flow can be seen or not when the inertial effect in terms of advection term is ignored in the considered model (from here onwards, called the DB model). If it appears, how does the advection term influence the instability mechanism? A comparative study between DB and DBA models is required. To do so, we have eliminated the advection term $({1}/{\chi ^2})(\boldsymbol {u}_{\boldsymbol {m}} \boldsymbol {\cdot } \boldsymbol {\nabla }_{\boldsymbol {m}}) \boldsymbol {u}_{\boldsymbol {m}}$ in the momentum equation (2.19) and a thorough analysis in terms of $\hat {d}$, $\chi$ and $\delta$ is made. Figure 7(a) represents the neutral stability curves for different values of $\hat {d}$ and 7(b) displays the energy budget spectrum as a function of $\hat {d}$ at critical point. Here, the values of all other parameters are kept the same as in figure 3(a). Similar to the DBA model, two lobes of neutral stability curve for $\hat {d} = 0.1$, 0.13 and $0.2$ are observed, and the least-stable $Re$ moves from the left to right lobe on increasing the value of $\hat {d}$. The critical value, $Re_c$, appears in the right lobe for $\hat {d}=0.13$ and $0.2$. Furthermore, in contrast to the DBA model, for $\hat {d} = 0.1$, the instability is observed for the entire range of $a$. Interestingly, as $\hat {d}$ is increased from 0.01 to 0.05, the critical value of $Re$ decreases, i.e. increasing fluid layer thickness destabilises the flow. However, further increasing of $\hat {d}$ causes the flow to be more stable, i.e. $Re_c$ increases as $\hat {d}$ increases within the range, $0.05\le \hat {d}\le 0.2$. Thus, the stabilising nature of $\hat {d}$, under the DBA model, is not strictly followed when the advective term is dropped in the momentum equation (see table 5). From figure 7(b), the transfer of kinetic energy via Reynolds stress to the basic flow in fluid and porous layers (i.e. $E_s$) is primarily balanced by $E_d$ ($E_{D_m}$) when $\hat {d}<0.055$ ($\hat {d}>0.055$). However, in the vicinity of $\hat {d}=0.055$, both $E_d$ and $E_{D_m}$ contribute equally. These result in fluid, porous and mixed modes for $\hat {d}<0.055$, $\hat {d}>0.055$ and in the neighbourhood of $0.055$, respectively. Note that in the range of $\hat {d}$ where the fluid mode prevails, the destabilising nature of $\hat {d}$ can be seen.

Figure 7. (a) Neutral stability curves for different values of $\hat {d}$; (b) energy components as a function of $\hat {d}$ eliminating advection term at $\delta =0.01$, $\chi =0.78$ and $\beta =0$.

Table 5. The value of critical Reynolds number for different values of $\hat {d}$ at $\delta =0.01$, $\chi =0.78$ and $\beta =0$.

The streamfunction patterns at the critical point for $\hat {d}=0.01$, $0.055$ and $0.2$ are shown in figure 8(a–c), respectively. It can be pointed out that, in the fluid mode, the patterns are primarily confined to the fluid layer. In the mixed mode, the patterns extend into both layers, but the penetration into the porous layer is minimal. In contrast, the porous mode exhibits patterns distributed almost equally between both layers.

Figure 8. The streamfunction pattern at $\delta =0.01$, $\chi =0.78$ and $\beta =0$: (a) $(a_c,Re_c)=(0.42,599.361)$, $\hat {d}=0.01$; (b) $(a_c,Re_c)=(0.77,310.850)$, $\hat {d}=0.055$; and (c) $(a_c,Re_c)=(2.33,3515.223)$, $\hat {d}=0.2$.

The effect of the advection term on flow instability for different porosity and permeability is analysed in figure 9. A comparative study on instability boundary in the $(\chi, Re_c)$-plane for DB as well as DBA models at $\delta =0.005$ and $0.01$ is made in figure 9(a,b), respectively. In contrast to a negligible change in $Re_c$ as a function of $\chi$ for $\delta =0.01$, a significant change in the same at $\delta =0.005$ under the consideration of the DBA model is observed. In addition, the change in $Re_c$ as a function $\chi$ under the DB model is negligible. For both values of $\delta$, the flow becomes more (less) unstable under the DB model for $\chi >0.62$ (<0.62). It is also seen that porosity stabilises the flow under the DBA model but under the DB model it first destabilises and then stabilises the flow. As we have already seen, increasing media permeability (depth ratio) destabilises (stabilises) the flow under the DBA model, but the influence of $\hat {d}$ on the flow stability under the DB model is not straightforward. A natural question that arises is whether the influence of $\delta$ under the DB model will remain straightforward or not. To shed more light in this direction, variation of $Re_c$ as a function $\delta$ is analysed in figure 10. It reveals that, for the DBA model, the critical Reynolds number ($Re_c$) decreases as the parameter $\delta$ increases. In contrast, when considering the DB model, $Re_c$ initially decreases with increasing $\delta$, followed by an increase as $\delta$ increases, which may be the consequence of mode change from porous to fluid.

Figure 9. Variation of $Re_c$ as a function of $\chi$ for $\hat {d}=0.1$ and $\beta =0$: (a) $\delta =0.005$ and (b) $\delta =0.01$.

Figure 10. (a) Variation of $Re_c$ and (b) energy components (DB model) as a function of $\delta$ at $\hat {d}=0.1$, $\chi =0.78$ and $\beta =0$.

It is worth mentioning here that the above theoretical prediction can be helpful in different engineering applications wherever Couette flow in a fluid overlying porous medium is encountered, specifically, the movement of ships in a port or shallow ocean. For example, the ship's propeller-induced flow mimics a scenario of Couette flow in fluid overlying a sedimented porous bottom (Kadir et al. 2024). To avoid damage to the aquatic ecosystem and sediment erosion, the ship's operator has to know the ship's appropriate maximum velocity, depth of water and nature of the seabed, i.e. quality of permeable sea bed, so that the fluid layers at the fluid–porous interface do not mix, i.e. the flow remains stable and smooth. This information will further optimise the pressure gradient at sediment and, thus, will help in preventing the erosion of sediment.

4. Conclusion

The current study examines the instability of isothermal Couette flow through a superposed fluid–porous system. The flow in the fluid layer is governed by the NS equation, whereas, in the porous layer, it is governed by the volume-averaged NS equation. Two situations have been considered: first, considering the inertial effect due to the advection term; and, second, ignoring the inertial effect due to the advection term. Using the Chebyshev spectral collocation method, the Orr–Sommerfeld eigenvalue problem is solved numerically. Even though it is known that the plane Couette flow in fluid overlying Darcy porous layer is always stable, its unstable behaviour is found for both the situations mentioned above. Three different modes are identified on the basis of the energy budget spectrum, and they are named as porous, fluid and mixed modes.

For the DBA model, the mode of instability changes at $\hat {d}\approx 0.05$ and $\delta \approx 0.02$ when $\beta =0$. A single lobe of the neutral curve corresponding to mixed mode is observed for $\delta =0.01$ and $0.01\le \hat {d}\le 0.05$. On further increasing the value of $\hat {d}$, two lobes of the neutral stability curve are seen and both lead to porous mode. It has been also noted that the critical value of $Re$ shifts from left to right lobe on increasing (decreasing) values of $\hat {d}\ (\delta )$. In this situation, a sudden increase of the contribution of $E_{d_m}$ and decrease of the same on $E_d$ in the energy balance are seen. The stress-jump coefficient changes instability characteristic significantly and reduces the critical value of $Re$ via energy production through stresses and velocities at the interface. Similar to plane Poiseuille flow (Deepu, Anand & Basu 2015), decreasing $\hat {d}$ (increasing $\delta$) increases the instability of the flow.

It has been found that in contrast to the DB model, for a relatively low permeable porous layer the critical value of $Re$ changes significantly as a function of $\chi$ under the DBA model. However, there exists a threshold value of 0.62 of $\chi$ at which the instability boundary under both models remains the same. Beyond this threshold value, the inertial effect delays the onset of instability. Furthermore, whenever the fluid mode of instability is encountered in a certain range of $\hat {d}~(\delta )$ under the DB model, the respective parameter acts as a destabilising (stabilising) factor.

Due to the lack of experimental work in this direction, the findings from the present study will also act as a stepping stone for experimentalists working in this direction. Furthermore, to have a deeper understanding of the flow mechanics that includes transitions to turbulence, a nonlinear stability analysis via cubic Landau theory (Sharma, Khandelwal & Bera 2018; Aleria, Khan & Bera 2024) or direct numerical simulations is required. These works are left for future study.