Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-24T02:13:01.800Z Has data issue: false hasContentIssue false
  • English
  • Français

Buoyant flow of 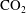$\text{CO}_{2}$ through and around a semi-permeable layer of finite extent

Published online by Cambridge University Press:  15 November 2016

Tri Dat Ngo ,
Emmanuel Mouche  and
Pascal Audigane
Tri Dat Ngo*
Affiliation:
Laboratoire des Sciences du Climat et de l’Environnement, UMR 8212 CEA-CNRS-UVSQ, C.E. de Saclay, F-91191 Gif-sur-Yvette CEDEX, France
Emmanuel Mouche
Affiliation:
Laboratoire des Sciences du Climat et de l’Environnement, UMR 8212 CEA-CNRS-UVSQ, C.E. de Saclay, F-91191 Gif-sur-Yvette CEDEX, France
Pascal Audigane
Affiliation:
Bureau des Recherches Géologiques et Minières, 3 Avenue Claude Guillemin – BP6009 – 45060 Orléans CEDEX 1, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The buoyancy- and capillary-driven counter-current flow of 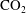$\text{CO}_{2}$ and brine through and around a semi-permeable layer is studied both numerically and theoretically. The continuities of the capillary pressure and the total flux at the interface between the permeable matrix and layer control the 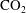$\text{CO}_{2}$ saturation discontinuity at the interface and the balance between the buoyant and capillary diffusion fluxes on each side of the interface. This interface process is first studied in a one-dimensional (1-D) vertical column geometry using the concept of extended capillary pressure and a graphical representation of the continuity conditions in the (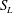$S_{L}$, 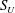$S_{U}$) plane, where 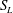$S_{L}$ and $S_{U}$ are the lower and upper saturation traces at the interface, respectively. In two dimensions, we heuristically extend the two-phase gravity current model to the case where the current is bounded by a semi-permeable layer. Consequently, the current is not saturated with 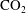$\text{CO}_{2}$, and its saturation and shape are derived from the flux and capillary pressure continuity conditions at the interface. This simplified model, which depends on 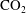$\text{CO}_{2}$ saturation only, is compared to fine grid simulations in the capillary-free and gravity-dominant cases. A good agreement is obtained in the second case; the current geometrical characteristics are accurately described. In the capillary-free case, we demonstrate that the local total velocity, which is, on average, zero because the flow is counter-current, must be considered in the total flux at the interface to obtain the same level of agreement.

JFM classification

Geophysical and Geological Flows: Gravity currents Multiphase and Particle-laden Flows: Multiphase flow Low-Reynolds-number flows: Porous media
Type
Papers
Information
Journal of Fluid Mechanics , Volume 809 , 25 December 2016 , pp. 553 - 584
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Acton, J. M., Huppert, H. E. & Worster, M. 2001 Two-dimensional viscous gravity currents flowing over a deep porous medium. J. Fluid Mech. 440, 359–380.Google Scholar
Adimurthi, Jaffré, J. & Veerappa Gowda, G. D. 2004 Godunov-type methods for conservation laws with a flux function discontinuous in space. SIAM J. Numer. Anal. 42 (1), 179–208.Google Scholar
Ambrose, W. A., Lakshminarasimhan, S., Holtz, M. H., Nunez-Lopez, V., Hovorka, S. D. & Duncan, I. 2008 Geologic factors controlling CO2 storage capacity and permanence: case studies based on experience with heterogeneity in oil and gas reservoirs applied to CO2 storage. Environ. Geol. 54 (8), 1619–1633.Google Scholar
Ames, W. F. 2014 Numerical Methods for Partial Differential Equations. Academic.Google Scholar
Andreianov, B. & Cancès, C. 2013 Vanishing capillarity solutions of buckley–leverett equation with gravity in two-rocks’ medium. Comput. Geosci. 17 (3), 551–572.CrossRefGoogle Scholar
Bear, J. 1988 Dynamics of Fluids in Porous Media. Dover.Google Scholar
Benson, S., Cook, P., Anderson, J., Bachu, S., Nimir, H. B., Basu, B., Bradshaw, J., Deguchi, G., Gale, J., von Goerne, G. et al. 2005 Underground geological storage. In IPCC Special Report on Carbon Dioxide Capture and Storage, pp. 195–276.Google Scholar
Bickle, M., Chadwick, A., Huppert, H. E., Hallworth, M. & Lyle, S. 2007 Modelling carbon dioxide accumulation at Sleipner: implications for underground carbon storage. Earth Planet. Sci. Lett. 255 (1), 164–176.Google Scholar
Brooks, R. H. & Corey, A. T. 1964 Hydraulic properties of porous media. In Hydrology Papers, Colorado State University.Google Scholar
Bryant, S. L., Lakshminarasimhan, S. & Pope, G. A. 2008 Buoyancy-dominated multiphase flow and its effect on geological sequestration of CO2 . SPE J. 13 (04), 447–454.Google Scholar
Buzzi, F., Lenzinger, M. & Schweizer, B. 2009 Interface conditions for degenerate two-phase flow equations in one space dimension. Anal. Intl Math. J. Anal. Appl. 29 (3), 299–316.Google Scholar
Cancès, C.2008 Two-phase flows in heterogeneous porous media: modeling and analysis of the flows of the effects involved by the discontinuities of the capillary pressure. PhD thesis, Université de Provence – Aix – Marseille I.Google Scholar
Cancès, C. 2010a Asymptotic behavior of two-phase flows in heterogeneous porous media for capillarity depending only on space. I. Convergence to the optimal entropy solution. SIAM J. Math. Anal. 42 (2), 946–971.Google Scholar
Cancès, C. 2010b Asymptotic behavior of two-phase flows in heterogeneous porous media for capillarity depending only on space. II. Non classical schocks to model oil-trapping. SIAM J. Math. Anal. 42 (2), 972–995.Google Scholar
Cancès, C., Gallouët, T. & Porretta, A. 2009 Two-phase flows involving capillary barriers in heterogeneous porous media. Interfaces Free Bound. 11, 239–258.Google Scholar
Celia, M. A., Bachu, S., Nordbotten, J. M. & Bandilla, K. W. 2015 Status of CO2 storage in deep saline aquifers with emphasis on modeling approaches and practical simulations. Water Resour. Res. 51 (9), 6846–6892.Google Scholar
Doughty, C. 2007 Modeling geologic storage of carbon dioxide: comparison of non-hysteretic and hysteretic characteristic curves. Energy Convers. Manage. 48 (6), 1768–1781.Google Scholar
Flemisch, B., Darcis, M., Erbertseder, K., Faigle, B., Lauser, A., Mosthaf, K., Müthing, S., Nuske, P., Tatomir, A., Wolff, M. et al. 2011 DuMu x : DUNE for multi-{phase, component, scale, physics, …} flow and transport in porous media. Adv. Water Resour. 34 (9), 1102–1112.Google Scholar
Golding, M. J., Huppert, H. E. & Neufeld, J. A. 2013 The effects of capillary forces on the axisymmetric propagation of two-phase, constant-flux gravity currents in porous media. Phys. Fluids 25 (3), 036602.Google Scholar
Golding, M. J., Neufeld, J. A., Hesse, M. A. & Huppert, H. E. 2011 Two-phase gravity currents in porous media. J. Fluid Mech. 678, 248–270.Google Scholar
Hayek, M., Mouche, M. & Mügler, C. 2009 Modeling vertical stratification of CO2 injected into a deep layered aquifer. Adv. Water Resour. 32 (3), 450–462.Google Scholar
Helmig, R. 1997 Multiphase Flow and Transport Processes in the Subsurface: a Contribution to the Modeling of Hydrosystems. Springer.Google Scholar
Hesse, M. A., Orr, F. M. & Tchelepi, H. A. 2008 Gravity currents with residual trapping. J. Fluid Mech. 611, 35–60.Google Scholar
Hesse, M. A., Tchelepi, H. A., Cantwel, B. J. & Orr, F. M. 2007 Gravity currents in horizontal porous layers: transition from early to late self-similarity. J. Fluid Mech. 577, 363–383.Google Scholar
Hesse, M. A. & Woods, A. W. 2010 Buoyant dispersal of CO2 during geological storage. Geophys. Res. Lett. 37 (1), L01403.Google Scholar
Honarpour, M. M., Koederitz, F. & Herbert, A. 1986 Relative Permeability of Petroleum Reservoirs. CRC.Google Scholar
Huppert, H. E. & Neufeld, J. A. 2014 The fluid mechanics of carbon dioxide sequestration. Annu. Rev. Fluid Mech. 46, 255–272.Google Scholar
Huppert, H. E. & Woods, A. W. 1995 Gravity-driven flows in porous layers. J. Fluid Mech. 292, 55–69.Google Scholar
Juanes, R., Macminn, C. W. & Szulczewski, M. L. 2010 The footprint of the CO2 plume during carbon dioxide storage in saline aquifers: storage efficiency for capillary trapping at the basin scale. Transp. Porous Med. 82 (1), 19–30.Google Scholar
Juanes, R., Spiteri, E. J., Orr, F. M. & Blunt, M. J. 2006 Impact of relative permeability hysteresis on geological CO2 storage. Water Resour. Res. 42 (12).Google Scholar
Kaasschieter, E. F. 1999 Solving the buckley-leverett equation with gravity in a heterogeneous porous medium. Comput. Geosci. 3 (1), 23–48.Google Scholar
Langtangen, H. P., Tveito, A. & Winther, R. 1992 Instability of Buckley-Leverett flow in a heterogeneous medium. Trans. Porous Med. 9 (3), 165–185.Google Scholar
Lengler, U., De Lucia, M. & Kühn, M. 2010 The impact of heterogeneity on the distribution of CO2 : numerical simulation of CO2 storage at Ketzin. Intl J. Greenh. Gas Control 4 (6), 1016–1025.Google Scholar
Lyle, S., Huppert, H. E., Hallworth, M., Bickle, M. & Chadwick, A. 2005 Axisymmetric gravity currents in a porous medium. J. Fluid Mech. 543, 293–302.Google Scholar
Mikelic, A., van Duijn, C. & Pop, I. 2002 Effective equations for two-phase flow with trapping on the micro scale. SIAM J. Appl. Maths 62 (5), 1531–1568.Google Scholar
Neufeld, J. A. & Huppert, H. E. 2009 Modelling carbon dioxide sequestration in layered strata. J. Fluid Mech. 625, 353–370.Google Scholar
Nordbotten, J. M. & Celia, M. A. 2006 Similarity solutions for fluid injection into confined aquifers. J. Fluid Mech. 561, 307–327.Google Scholar
Pritchard, D., Woods, A. W. & Hogg, A. J. 2001 On the slow draining of a gravity current moving through a layered permeable medium. J. Fluid Mech. 444, 23–47.CrossRefGoogle Scholar
Spannuth, M. J., Neufeld, J. A., Wettlaufer, J. S. & Worster, M. 2009 Axisymmetric viscous gravity currents flowing over a porous medium. J. Fluid Mech. 622, 135–144.Google Scholar
Van Duijn, C. J. & De Neef, M. J. 1998 Similarity solution for capillary redistribution of two phases in a porous medium with a single discontinuity. Adv. Water Resour. 21 (6), 451–461.Google Scholar
Van Duijn, C. J., Molenaar, J. & De Neef, M. J. 1995 The effect of capillary forces on immiscible two-phase flow in heterogeneous porous media. Trans. Porous Med. 21 (1), 71–93.Google Scholar
Van Genuchten, M. Th. 1980 A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Science Soc. Am. J. 44 (5), 892–898.Google Scholar
Vella, D. & Huppert, H. E. 2006 Gravity currents in a porous medium at an inclined plane. J. Fluid Mech. 555, 353–362.Google Scholar
Woods, A. W. & Farcas, A. 2009 Capillary entry pressure and the leakage of gravity currents through a sloping layered permeable rock. J. Fluid Mech. 618, 361–379.Google Scholar