Buoyancy-induced turbulent mixing in a narrow tilted tank

Abstract

We describe a series of experiments in which a constant buoyancy flux 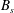$B_{s}$ of salty dyed water of density 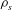${\it\rho}_{s}$ is introduced at the top of a long narrow tank of square cross-section tilted at an angle 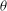${\it\theta}$ to the vertical. The tank is initially filled with fresh clear water of density 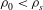${\it\rho}_{0}<{\it\rho}_{s}$, and we investigate the resulting buoyancy-driven turbulent mixing at various tilt angles 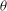${\it\theta}$. Using a light-attenuation image analysis method, we determine the evolution of the reduced gravity 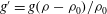$g^{\prime }=g({\it\rho}-{\it\rho}_{0})/{\it\rho}_{0}$ of the mixed fluid in time and space as it propagates towards the bottom of the tank. 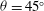For all tilt angles tested (${\it\theta}=0^{\circ }$ to ${\it\theta}=45^{\circ }$), we focus exclusively on high-Reynolds-number experiments, where the flow remains turbulent both along the length and across the width of the tank. We find that when 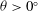${\it\theta}>0^{\circ }$, the cross-tank component of gravity acts to segregate the dense fluid from the relatively lighter fluid, and a statically stable gradient of 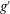$g^{\prime }$ across the width of the tank occurs more frequently than a statically unstable gradient, i.e. $(\partial g^{\prime }/\partial x)<0$ occurs more frequently than 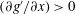$(\partial g^{\prime }/\partial x)>0$. This is in contrast to the case when 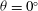${\it\theta}=0^{\circ }$, where instantaneous cross-tank gradients of reduced gravity may be positive or negative, but are equal to zero in an ensemble average. We observe that when 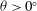${\it\theta}>0^{\circ }$, the cross-tank gradient of reduced gravity induces a turbulent counterflow where dense fluid flows down the upward-facing surface of the tank and lighter fluid flows in the opposing direction above. We model the evolution of the cross-tank averaged, ensemble averaged reduced gravity 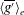$\langle \overline{g^{\prime }}\rangle _{e}$ as a diffusive process using Prandtl’s mixing length theory, building on the model of van Sommeren et al. (J. Fluid Mech., vol. 701, 2012, pp. 278–303) who considered purely vertical tanks. We model the fluctuations (from the cross-tank averaged quantity) of reduced gravity 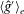$\langle {\hat{g}}^{\prime }\rangle _{e}$ and counterflow velocity 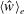$\langle {\hat{w}}\rangle _{e}$ by characterising the mixing across the width of the tank with a cross-tank turbulent diffusivity 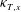${\it\kappa}_{T,x}$, which we assume is constant in the cross-tank coordinate $x$. We show that the counterflow that exists when 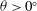${\it\theta}>0^{\circ }$ acts directly to enhance the effective along-tank turbulent diffusivity ${\it\kappa}_{T,z}$, and from experiments, we find that the mixing length increases approximately linearly with 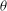${\it\theta}$, and that both 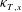${\it\kappa}_{T,x}$ and 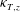${\it\kappa}_{T,z}$ are proportional to 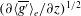$(\partial \langle \overline{g^{\prime }}\rangle _{e}/\partial z)^{1/2}$.