Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-24T23:06:46.408Z Has data issue: false hasContentIssue false
  • English
  • Français

Buoyancy-driven destabilization of an immersed granular bed

Published online by Cambridge University Press:  26 March 2018

Eric Herbert ,
Cyprien Morize ,
Aurélie Louis-Napoléon ,
Christophe Goupil ,
Pierre Jop  and
Yves D’Angelo Open the ORCID record for Yves D’Angelo [Opens in a new window]
Eric Herbert
Affiliation:
DyCo Team, Laboratoire Interdisciplinaire des Energies de Demain, Université Paris Diderot, CNRS, 75013 Paris, France
Cyprien Morize
Affiliation:
Laboratoire FAST, CNRS, Université Paris-Sud, Université Paris-Saclay, 91405, Orsay, France
Aurélie Louis-Napoléon
Affiliation:
Institut de Mécanique des Fluides de Toulouse, IMFT, Université de Toulouse, CNRS, 31400 Toulouse, France
Christophe Goupil
Affiliation:
DyCo Team, Laboratoire Interdisciplinaire des Energies de Demain, Université Paris Diderot, CNRS, 75013 Paris, France
Pierre Jop
Affiliation:
Surface du verre et Interfaces, CNRS/Saint-Gobain, 93300 Aubervilliers, France
Yves D’Angelo*
Affiliation:
DyCo Team, Laboratoire Interdisciplinaire des Energies de Demain, Université Paris Diderot, CNRS, 75013 Paris, France Université Côte d’Azur, Laboratory Mathematics & Interactions LJAD, UNS/CNRS, 06108 Nice, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Under suitable conditions, an immersed granular bed can be destabilized by local thermal forcing and the induced buoyant force. The destabilization is evident from the triggering and establishment of a dense fluid-like granular plume. Varying the initial granular layer average height 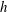$h$, a time series of the free layer surface is extracted, allowing us to dynamically compute the underlying volume of the granular layer. Different observed phenomena, namely the initial interface deformation, the lowering of the average granular interface (i.e. decrease of the granular layer volume) and the emission of a plume, are analysed. We show that the phenomenon is mainly driven by heat transfer, for large 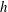$h$ and also involves a variable height thermal boundary condition and Darcy flow triggering, for small 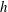$h$. Simple modelling with no adjustable parameters not only allows us to capture the observed scaling power laws but is also in quantitative agreement with the obtained experimental data.

JFM classification

Convection: Buoyancy-driven instability Convection: Convection in porous media Granular media: Granular media
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 843 , 25 May 2018 , pp. 778 - 809
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Al-mashhadani, M. K. H., Wilkinson, S. J. & Zimmerman, W. B. 2016 Carbon dioxide rich microbubble acceleration of biogas production in anaerobic digestion. Chem. Engng Sci. 156 (Supplement C), 24–35.Google Scholar
Alobaid, F., Baraki, N. & Epple, B. 2014 Investigation into improving the efficiency and accuracy of CFD/DEM simulations. Particuology 16, 41–53.Google Scholar
Amritkar, A., Deb, S. & Tafti, D. 2014 Efficient parallel CFD-DEM simulations using OpenMP. J. Comput. Phys. 256, 501–519.Google Scholar
An, X. Z., Li, C. X., Yang, R. Y., Zou, R. P. & Yu, A. B. 2009 Experimental study of the packing of mono-sized spheres subjected to one-dimensional vibration. Powder Technol. 196 (1), 50–55.Google Scholar
Andrews, D. J. 2002 A fault constitutive relation accounting for thermal pressurization of pore fluid. J. Geophys. Res. 107 (B12).Google Scholar
Badr, S., Gauthier, G. & Gondret, Ph. 2016 Crater jet morphology. Phys. Fluids 28 (3), 033305.Google Scholar
Blumenfeld, R., Amitai, S., Jordan, J. F. & Hihinashvili, R. 2016 Failure of the volume function in granular statistical mechanics and an alternative formulation. Phys. Rev. Lett. 116, 148001.Google Scholar
Boyer, F., Guazzelli, É. & Pouliquen, O. 2011 Unifying suspension and granular rheology. Phys. Rev. Lett. 107, 188301.Google Scholar
Caricchi, L., Burlini, L., Ulmer, P., Gerya, T., Vassalli, M. & Papale, P. 2007 Non-Newtonian rheology of crystal-bearing magmas and implications for magma ascent dynamics. Earth Planet. Sci. Lett. 264 (3), 402–419.Google Scholar
Cassar, C., Nicolas, M. & Pouliquen, O. 2005 Submarine granular flows down inclined planes. Phys. Fluids 11, 103301.Google Scholar
Champallier, R., Bystricky, M. & Arbaret, L. 2008 Experimental investigation of magma rheology at 300 mpa: from pure hydrous melt to 76 vol.% of crystals. Earth Planet. Sci. Lett. 267 (3), 571–583.Google Scholar
Chauchat, J. & Médale, M. 2014 A three-dimensional numerical model for dense granular flows based on the 𝜇(I)-rheology. J. Comput. Phys. 256, 696–712.Google Scholar
Cook, M. A. & Mortensen, K. S. 1967 Impact cratering in granular materials. J. Appl. Phys. 38 (13), 5125–5128.Google Scholar
Coulais, C., Seguin, A. & Dauchot, O. 2014 Shear modulus and dilatancy softening in granular packings above jamming. Phys. Rev. Lett. 113, 198001.Google Scholar
Courrech du Pont, S., Gondret, Ph., Perrin, B. & Rabaud, M. 2003 Granular avalanches in fluids. Phys. Rev. Lett. 90 (4), 044301.Google Scholar
Cundall, P. A. & Strack, O. D. L. 1979 A discrete numerical model for granular assemblies. Géotechnique 29 (1), 47–65.Google Scholar
Degruyter, W. & Huber, C. 2014 A model for eruption frequency of upper crustal silicic magma chambers. Earth Planet. Sci. Lett. 403 (Supplement C), 117–130.Google Scholar
Elderfield, H. & Schultz, A. 1996 Mid-ocean ridge hydrothermal fluxes and the chemical composition of the ocean. Annu. Rev. Earth Planet. Sci. 24 (1), 191–224.Google Scholar
Farrell, G. R., Martini, K. M. & Menon, N. 2010 Loose packings of frictional spheres. Soft Matt. 6, 2925–2930.Google Scholar
Fraggedakis, D., Dimakopoulos, Y. & Tsamopoulos, J. 2016 Yielding the yield stress analysis: a thorough comparison of recently proposed elasto-visco-plastic (EVP) fluid models. J. Non-Newtonian Fluid Mech. 238, 170–188.Google Scholar
GDR MiDi 2004 On dense granular flows. Eur. Phys. J. E 14 (4), 341–365.Google Scholar
Guazzelli, É & Hinch, J. 2011 Fluctuations and instability in sedimentation. Annu. Rev. Fluid Mech. 43, 97–116.Google Scholar
Guo, Y. & Sinclair Curtis, J. 2015 Discrete element method simulations for complex granular flows. Annu. Rev. Fluid Mech. 47 (1), 21–46.Google Scholar
Jajcevic, D., Siegmann, E., Radeke, Ch. & Khinast, J. G. 2013 Large-scale CFD-DEM simulations of fluidized granular systems. Chem. Engng Sci. 98, 298–310.Google Scholar
Jop, P., Forterre, Y. & Pouliquen, O. 2006 A constitutive law for dense granular flows. Nature 441 (7094), 727–730.Google Scholar
Karimfazli, I., Frigaard, I. A. & Wachs, A. 2016 Thermal plumes in viscoplastic fluids: flow onset and development. J. Fluid Mech. 787, 474–507.Google Scholar
Kaviany, M. 1995 Principles of Heat Transfer in Porous Media, 2nd edn. Springer.Google Scholar
Khanal, M. & Jayasundara, C. T. 2014 Role of particle stiffness and inter-particle sliding friction in milling of particles. Particuology 16, 54–59.Google Scholar
Kiesgen de Richter, S., Hanotin, C., Marchal, P., Leclerc, S., Demeurie, F. & Louvet, N. 2015 Vibration-induced compaction of granular suspensions. Eur. Phys. J. E 38 (7), 74.Google Scholar
Kloss, Ch., Goniva, Ch., Hager, A., Amberger, S. & Pirker, S. 2012 Models, algorithms and validation for opensource DEM and CFD-DEM. Prog. Comput. Fluid Dyn. 12 (2/3), 140–152.Google Scholar
Lagrée, P.-Y., Staron, L. & Popinet, S. 2011 The granular column collapse as a continuum: validity of a two-dimensional Navier–Stokes model with a 𝜇(I)-rheology. J. Fluid Mech. 686, 378–408.Google Scholar
Lavorel, G. & Le Bars, M. 2009 Sedimentation of particles in a vigorously convecting fluid. Phys. Rev. E 80 (4), 046324.Google Scholar
Loranca-Ramos, F. E., Carrillo-Estrada, J. L. & Pacheco-Vázquez, F. 2015 Craters and granular jets generated by underground cavity collapse. Phys. Rev. Lett. 115, 028001.Google Scholar
Maréchal, E.2016 Clogging of jet-engine fuel systems by dense suspensions of ice particles. PhD thesis - Ecole nationale supérieure d’arts et métiers – ENSAM.Google Scholar
Marsh, B. D. 1981 On the crystallinity, probability of occurrence, and rheology of lava and magma. Contrib. Mineral. Petrol. 78 (1), 85–98.Google Scholar
Martin, D. & Nokes, R. 1988 Crystal settling in a vigorously converting magma chamber. Nature 332 (6164), 534–536.Google Scholar
Martin, D. & Nokes, R. 1989 A fluid-dynamic study of crystal settling in convecting magmas. J. Petrol. 30 (6), 1471–1500.Google Scholar
Mena, S. E., Luu, L.-H., Cuéllar, P., Philippe, P. & Sinclair Curtis, J. 2017 Parameters affecting the localized fluidization in a particle medium. AIChE J. 63 (5), 1529–1542.Google Scholar
Morize, C., Herbert, E. & Sauret, A. 2017 Resuspension threshold of a granular bed by localized heating. Phys. Rev. E 96, 032903.Google Scholar
Mutlu Sumer, B., Hatipoglu, F., Fredsøe, J. & Kaan Sumer, S. 2006 The sequence of sediment behaviour during wave-induced liquefaction. Sedimentology 53 (3), 611–629.Google Scholar
Ngoma, J., Philippe, P., Bonelli, S., Delenne, J.-Y. & Radjai, F. 2015 Interaction Between Two Localized Fluidization Cavities in Granular Media: Experiments and Numerical Simulation (ed. Soga, K., Kumar, K., Biscontin, G. & Kuo, M.). CRC Press and Taylor and Francis.Google Scholar
Philippe, P. & Badiane, M. 2013 Localized fluidization in a granular medium. Phys. Rev. E 87, 042206.Google Scholar
Pouliquen, O., Belzons, M. & Nicolas, M. 2003 Fluctuating particle motion during shear induced granular compaction. Phys. Rev. Lett. 91 (1), 014301.Google Scholar
Rigord, P., Guarino, A., Vidal, V. & Géminard, J.-C. 2005 Localized instability of a granular layer submitted to an ascending liquid flow. Granul. Matt. 7 (4), 191–197.Google Scholar
Rumpf, H. & Gupte, A.R. 1975 The influence of porosity and grain size distribution on the permeability equation of porous flow. Chemie Ing. Techn. 43 (6), 367–375.Google Scholar
Sable, J. E., Houghton, B. F., Del Carlo, P. & Coltelli, M. 2006 Changing conditions of magma ascent and fragmentation during the Etna 122_BC basaltic Plinian eruption: evidence from clast microtextures. J. Volcanol. Geotherm. Res. 158 (3–4), 333–354.Google Scholar
Saramito, P. & Wachs, A. 2017 Progress in numerical simulation of yield stress fluid flows. Rheol. Acta 56 (3), 211–230.Google Scholar
Seguin, A., Bertho, Y., Gondret, P. & Crassous, J. 2009 Sphere penetration by impact in a granular medium: a collisional process. Eur. Phys. Lett. 88 (4), 44002.Google Scholar
Shibano, Y., Ikuro, S. & Namiki, A. 2013 A laboratory model for melting erosion of a magma chamber roof and the generation of a rhythmic layering. J. Geophys. Res. 118, 4101–4116.Google Scholar
Solomatov, V. S., Olson, P. & Stevenson, D. J. 1993 Entrainment from a bed of particles by thermal convection. Earth Planet. Sci. Lett. 120 (3), 387–393.Google Scholar
Stroh, A., Alobaid, F., Hasenzahl, M. T., Hilz, J., Strohle, J. & Epple, B. 2016 Comparison of three different CFD methods for dense fluidized beds and validation by a cold flow experiment. Particuology 29, 34–47.Google Scholar
Testu, A., Didierjean, S., Maillet, D., Moyne, C., Metzger, T. & Niass, T. 2007 Thermal dispersion for water or air flow through a bed of glass beads. Intl J. Heat Mass Transfer 50 (7–8), 1469–1484.Google Scholar
Varas, G., Vidal, V. & Géminard, J.-Ch. 2009 Dynamics of crater formations in immersed granular materials. Phys. Rev. E 79, 021301.Google Scholar
Verhoeven, J. & Schmalzl, J. 2009 A numerical method for investigating crystal settling in convecting magma chambers. Geochem. Geophys. Geosyst. 10, Q12007.Google Scholar
Woods, A. W. 1998 Observations and models of volcanic eruption columns. Geological Society, London, Special Publications 145 (1), 91–114.Google Scholar
Woods, A. W. & Wohletz, K. 1991 Dimensions and dynamics of co-ignimbrite eruption columns. Nature 350 (6315), 225–227.Google Scholar
Zhang, H.-L., Chen, G.-H. & Han, S.-J. 1997 Viscosity and density of H2 O + NaCl + CaCl2 and H2 O + KCl + CaCl2 at 298.15 K. J. Chem. Engng Data 42 (3), 526–530.Google Scholar
Zhao, R., Zhang, Q., Tjugito, H. & Cheng, X. 2015 Granular impact cratering by liquid drops: understanding raindrop imprints through an analogy to asteroid strikes. Proc. Natl Acad. Sci. USA 112 (2), 342–347.Google Scholar
Zoueshtiagh, F. & Merlen, A. 2007 Effect of a vertically flowing water jet underneath a granular bed. Phys. Rev. E 75, 056313.Google Scholar

Herbert et al. supplementary movie

A typical long-run (total) evolution of the thermal destabilization and grain particles re-suspension of the granular layer, for an initial length h = 23 mm and $\Delta$ = 45 K, showing the different stages of the process. Note that the movie time is accelerated: 1 s in the movie corresponds to 12.5 s in physical time.

Download Herbert et al. supplementary movie(Video)
Video 318.6 MB