Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-14T11:15:57.826Z Has data issue: false hasContentIssue false
  • English
  • Français

Bubble breakup simulation in nozzle flows

Published online by Cambridge University Press:  23 August 2012

Oleg E. Ivashnyov  and
Marina N. Ivashneva
Oleg E. Ivashnyov
Affiliation:
Department of Gas and Wave Dynamics, Faculty of Mechanics and Mathematics, Moscow MV Lomonosov State University, Moscow 119899, Russia
Marina N. Ivashneva*
Affiliation:
Department of Gas and Wave Dynamics, Faculty of Mechanics and Mathematics, Moscow MV Lomonosov State University, Moscow 119899, Russia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Experiments on high-pressure vessel decompression have shown that vaporization occurs in ‘boiling shocks’ moving with a velocity of 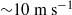. To explain this phenomenon, a model accounting for bubble breakup was suggested (Ivashnyov, Ivashneva & Smirnov, J. Fluid. Mech., vol. 413, 2000, pp. 149–180). It was shown that the explosive boiling was caused by chain bubble fragmentation, which led to a sharp increase in the interface area and instantaneous transformation of the mixture into an equilibrium state. In the present study, this model is used to simulate nozzle flows with no change in the free parameters chosen earlier for modelling a tube decompression. It is shown that an advanced model ensures the best correspondence to experiments for flashing flows in comparison with an equilibrium model and with a model of boiling at a constant number of centres. It is also shown that the formation of a boiling shock in a critical nozzle flow leads to autovibrations.

JFM classification

Drops and Bubbles: Boiling Compressible Flows: Shock waves
Type
Papers
Information
Journal of Fluid Mechanics , Volume 710 , 10 November 2012 , pp. 72 - 101
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Bauer, E., Houdauer, G. & Sureau, H. 1977 Interprétation des essays Moby-Dick à l’aide de modèles prenant en compte les déséquilibres thermodynamiques. European Two Phase Flow Group Meeting, Grenoble.Google Scholar
2. Bilicki, Z., Dafermos, C., Kestin, J., Majda, G. & Zeng, D. L. 1987 Trajectories and singular points in steady-state models of two-phase flows. Intl J. Multiphase Flow 13 (4), 511–533.Google Scholar
3. Birkhoff, G. 1960 Hydrodynamics. Princeton University Press.Google Scholar
4. Boivin, J. Y. 1979 Two-phase critical flow in long nozzles. Nucl. Technol. 46 (3), 540–545.CrossRefGoogle Scholar
5. Drew, D. A. & Passman, S. L. 1998 Theory of Multicomponent Fluids. Springer.Google Scholar
6. Edwards, A. R. & O’Brien, T. P. 1970 Studies on phenomena connected with the depressurization of water reactors. J. Br. Nucl. Engng Soc. 9, 125–135.Google Scholar
7. Giot, M. 1981 Critical flows. In Thermohydraulics of two-phase systems for industrial design and nuclear engineering (ed. Delhaye, J. M., Giot, M. & Reithmuller, M. L. ), pp. 405–452. Hemisphere.Google Scholar
8. Henry, R. E. 1968 A study of one- and two-component, two-phase critical flows at low qualities. Report ANL-7430.CrossRefGoogle Scholar
9. Isaev, O. A. 1980 Liquid boiling under a fast pressure fall in an adiabatic unsteady stream. Doctor’s thesis, Sverdlovsk.Google Scholar
10. Isbin, H. S. 1980 Some observation on the status of two-phase critical flow models. Intl J. Multiphase Flow 6, 131–137.CrossRefGoogle Scholar
11. Ishii, M. & Hibiki, T. 2006 Thermo-Fluid Dynamics of Two-Phase Flow. Springer.CrossRefGoogle Scholar
12. Ivandaev, A. I. & Gubaidullin, A. A. 1978 The investigation of an unsteady efflux of boiling liquid in a thermodynamically equilibrium approximation. Teplofiz. Vys. Temp. 16 (3), 556–562 (in Russian).Google Scholar
13. Ivashnyov, O. E., Ivashneva, M. N. & Smirnov, N. N. 2000 Slow waves of boiling under hot water depressurization. J. Fluid Mech. 413, 149–180.CrossRefGoogle Scholar
14. Ivashnyov, O. E. & Soplenkov, K. I. 1992 A model involving break-up to explain peculiarities of boiling liquid efflux process. Intl J. Multiphase Flow 18 (5), 727–738.CrossRefGoogle Scholar
15. Labuntsov, D. A. & Avdeev, A. A. 1981 Theory of boiling discontinuity. Teplofiz. Vys. Temp. 19 (3), 552–556 (in Russian).Google Scholar
16. Labuntsov, D. A. & Avdeev, A. A. 1982 The mechanism of flow choking at impact boiling of liquid. Teplofiz. Vys. Temp. 20 (1), 88–96 (in Russian).Google Scholar
17. Lamb, G. 1957 Hydrodynamics. Cambridge University Press.Google Scholar
18. Lienhard, J. H., Alangir, M. & Trela, M. 1978 Early response of hot water to sudden release from high pressure. Trans. ASME: J. Heat Transfer 100 (3), 473–479.Google Scholar
19. Nigmatulin, R. I. 1991 Dynamics of Multiphase Media, Vols I, II. Hemisphere.Google Scholar
20. Nigmatulin, R. I. & Soplenkov, K. I. 1980 The study of an unsteady efflux of boiling liquid from channels in the thermodynamically non-equilibrium approximation. Teplofiz. Vys. Temp. 18 (1), 118–131 (in Russian).Google Scholar
21. Scriven, L. E. 1959 On the dynamics of phase growth. Chem. Engng Sci. 10 (1–2), 1–13.CrossRefGoogle Scholar
22. Sivuchin, D. V. 1979 The Course of Fundamental Physics. Thermodynamics and Molecular Physics. Nauka (in Russian).Google Scholar
23. Skorek, T. & Papadimitriou, P. 1997 A simple model for critical flashing flows in nozzles: development and experimental verification. In Experimental Heat Transfer, Fluid Mechanics and Thermodynamics 1997 (ed. Giot, M., Mayinger, F. & Celata, G.P. ), pp. 1701–1708. Edizioni ETS.Google Scholar
24. Vaisman, M. L. 1967 Thermodynamics of Vapor–Liquid Flows. Energiya (in Russian).Google Scholar
25. Winters, W. S. Jr & Merte, H. Jr 1979 Experiments and nonequilibrium analysis of pipe blowdown. Nucl. Sci. Engng 69 (3), 411–429.CrossRefGoogle Scholar