Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-28T16:20:54.099Z Has data issue: false hasContentIssue false
  • English
  • Français

Bounds for convection between rough boundaries

Published online by Cambridge University Press:  09 September 2016

David Goluskin  and
Charles R. Doering
David Goluskin*
Affiliation:
Department of Mathematics and Center for the Study of Complex Systems, University of Michigan, Ann Arbor, MI 48109, USA
Charles R. Doering
Affiliation:
Department of Mathematics and Center for the Study of Complex Systems, University of Michigan, Ann Arbor, MI 48109, USA Department of Physics, University of Michigan, Ann Arbor, MI 48109, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider Rayleigh–Bénard convection in a layer of fluid between rough no-slip boundaries where the top and bottom boundary heights are functions of the horizontal coordinates with square-integrable gradients. We use the background method to derive an upper bound on the mean heat flux across the layer for all admissible boundary geometries. 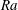This flux, normalized by the temperature difference between the boundaries, can grow with the Rayleigh number ($Ra$) no faster than 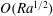$O(Ra^{1/2})$ as 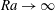$Ra\rightarrow \infty$. Our analysis yields a family of similar bounds, depending on how various estimates are tuned, but every version depends explicitly on the boundary geometry. In one version the coefficient of the 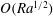$O(Ra^{1/2})$ leading term is 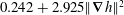$0.242+2.925\Vert \unicode[STIX]{x1D735}h\Vert ^{2}$, where 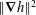$\Vert \unicode[STIX]{x1D735}h\Vert ^{2}$ is the mean squared magnitude of the boundary height gradients. Application to a particular geometry is illustrated for sinusoidal boundaries.

JFM classification

Mathematical Foundations: Variational methods
Type
Papers
Information
Journal of Fluid Mechanics , Volume 804 , 10 October 2016 , pp. 370 - 386
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Busse, F. H. 1969 Bounds on the transport of mass and momentum by turbulent flow between parallel plates. Z. Angew. Math. Phys. 20, 1–14.Google Scholar
Choffrut, A., Nobili, C. & Otto, F. 2016 Upper bounds on Nusselt number at finite Prandtl number. J. Differ. Equ. 260, 3860–3880.CrossRefGoogle Scholar
Ciliberto, S. & Laroche, C. 1999 Random roughness of boundary increases the turbulent convection scaling exponent. Phys. Rev. Lett. 82, 3998–4001.CrossRefGoogle Scholar
Constantin, P. & Doering, C. R. 1994 Variational bounds on energy dissipation in incompressible flows: shear flow. Phys. Rev. E 49, 4087–4099.Google Scholar
Constantin, P. & Doering, C. R. 1995 Variational bounds on energy dissipation in incompressible flows. II: channel flow. Phys. Rev. E 51, 3192–3198.Google ScholarPubMed
Constantin, P. & Doering, C. R. 1996 Variational bounds on energy dissipation in incompressible flows. III: convection. Phys. Rev. E 53, 5957–5981.Google Scholar
Du, Y.-B. & Tong, P. 1998 Enhanced heat transport in turbulent convection over a rough surface. Phys. Rev. Lett. 81, 987–990.Google Scholar
Du, Y.-B. & Tong, P. 2000 Turbulent thermal convection in a cell with ordered rough boundaries. J. Fluid Mech. 407, 57–84.Google Scholar
Goluskin, D. 2015a Internally Heated Convection and Rayleigh–Bénard Convection. Springer.Google Scholar
Goluskin, D. 2015b Internally heated convection beneath a poor conductor. J. Fluid Mech. 771, 36–56.CrossRefGoogle Scholar
Hoffmann, N. P. & Vitanov, N. K. 1999 Upper bounds on energy dissipation in Couette–Ekman flow. Phys. Lett. A 255, 277–286.Google Scholar
Howard, L. N. 1963 Heat transport by turbulent convection. J. Fluid Mech. 17, 405–432.CrossRefGoogle Scholar
Howard, L. N. 1972 Bounds on flow quantities. Annu. Rev. Fluid Mech. 4, 473–494.Google Scholar
Jeffreys, H. 1928 Some cases of instability in fluid motion. Proc. R. Soc. Lond. A 118, 195–208.Google Scholar
Johnston, H. & Doering, C. R. 2009 Comparison of turbulent thermal convection between conditions of constant temperature and constant flux. Phys. Rev. Lett. 102, 064501.Google Scholar
Kerswell, R. R. 1997 Variational bounds on shear-driven turbulence and turbulent Boussinesq convection. Phys. D 100, 355–376.Google Scholar
Kerswell, R. R. 2001 New results in the variational approach to turbulent Boussinesq convection. Phys. Fluids 13, 192–209.Google Scholar
Kerswell, R. R. 2002 Upper bounds on general dissipation functionals in turbulent shear flows: revisiting the ‘efficiency’ functional. J. Fluid Mech. 461, 239–275.Google Scholar
Lu, L., Doering, C. R. & Busse, F. H. 2004 Bounds on convection driven by internal heating. J. Math. Phys. 45, 2967–2986.Google Scholar
Nicodemus, R., Grossmann, S. & Holthaus, M. 1998 The background flow method. Part 1. Constructive approach to bounds on energy dissipation. J. Fluid Mech. 363, 281–300.Google Scholar
Otero, J., Wittenberg, R. W., Worthing, R. A. & Doering, C. R. 2002 Bounds on Rayleigh–Bénard convection with an imposed heat flux. J. Fluid Mech. 473, 191–199.CrossRefGoogle Scholar
Otto, F. & Seis, C. 2011 Rayleigh–Bénard convection: improved bounds on the Nusselt number. J. Math. Phys. 52, 083702.Google Scholar
Plasting, S. C. & Ierley, G. R. 2005 Infinite-Prandtl-number convection. Part 1. Conservative bounds. J. Fluid Mech. 542, 343–363.CrossRefGoogle Scholar
Plasting, S. C. & Kerswell, R. R. 2003 Improved upper bound on the energy dissipation rate in plane Couette flow: the full solution to Busse’s problem and the Constantin–Doering–Hopf problem with one-dimensional background field. J. Fluid Mech. 477, 363–379.Google Scholar
Lord Rayleigh 1916 On convection currents in a horizontal layer of fluid, when the higher temperature is on the under side. Phil. Mag. 32 (192), 529–546.CrossRefGoogle Scholar
Roche, P. E., Castaing, B., Chabaud, B. & Hébral, B. 2001 Observation of the 1/2 power law in Rayleigh–Bénard convection. Phys. Rev. E 63, 045303.Google Scholar
Salort, J., Liot, O., Rusaouen, E., Seychelles, F., Tisserand, J.-C., Creyssels, M., Castaing, B. & Chillà, F. 2014 Thermal boundary layer near roughnesses in turbulent Rayleigh–Bénard convection: flow structure and multistability. Phys. Fluids 26, 015112.CrossRefGoogle Scholar
Seis, C. 2015 Scaling bounds on dissipation in turbulent flows. J. Fluid Mech. 777, 591–603.Google Scholar
Stringano, G., Pascazio, G. & Verzicco, R. 2006 Turbulent thermal convection over grooved plates. J. Fluid Mech. 557, 307–336.Google Scholar
Toppaladoddi, S., Succi, S. & Wettlaufer, J. S. 2015 Tailoring boundary geometry to optimize heat transport in turbulent convection. Europhys. Lett. 111, 44005.Google Scholar
Villermaux, E. 1998 Transfer at rough sheared interfaces. Phys. Rev. Lett. 81, 4859–4862.CrossRefGoogle Scholar
Wagner, S. & Shishkina, O. 2015 Heat flux enhancement by regular surface roughness in turbulent thermal convection. J. Fluid Mech. 763, 109–135.CrossRefGoogle Scholar
Wang, X. M. 1997 Time averaged energy dissipation rate for shear driven flows in ℝ n . Phys. D 99, 555–563.Google Scholar
Wang, X. M. & Whitehead, J. P. 2013 A bound on the vertical transport of heat in the ‘ultimate state’ of slippery convection at large Prandtl numbers. J. Fluid Mech. 729, 103–122.Google Scholar
Wei, P., Chan, T.-S., Ni, R., Zhao, X.-Z. & Xia, K.-Q. 2014 Heat transport properties of plates with smooth and rough surfaces in turbulent thermal convection. J. Fluid Mech. 740, 28–46.Google Scholar
Wen, B., Chini, G. P., Dianati, N. & Doering, C. R. 2013 Computational approaches to aspect-ratio-dependent upper bounds and heat flux in porous medium convection. Phys. Lett. A 377, 2931–2938.CrossRefGoogle Scholar
Whitehead, J. P. & Doering, C. R. 2011a Internal heating driven convection at infinite Prandtl number. J. Math. Phys. 52, 093101.Google Scholar
Whitehead, J. P. & Doering, C. R. 2011b Ultimate state of two-dimensional Rayleigh–Bénard convection between free-slip fixed-temperature boundaries. Phys. Rev. Lett. 106, 244501.Google Scholar
Whitehead, J. P. & Doering, C. R. 2012 Rigid bounds on heat transport by a fluid between slippery boundaries. J. Fluid Mech. 707, 241–259.Google Scholar
Whitehead, J. P. & Wittenberg, R. W. 2014 A rigorous bound on the vertical transport of heat in Rayleigh–Bénard convection at infinite Prandtl number with mixed thermal boundary conditions. J. Math. Phys. 55, 093104.Google Scholar
Wittenberg, R. W. 2010 Bounds on Rayleigh–Bénard convection with imperfectly conducting plates. J. Fluid Mech. 665, 158–198.CrossRefGoogle Scholar