Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-12-01T01:30:50.188Z Has data issue: false hasContentIssue false
  • English
  • Français

Boundary layer fluctuations in turbulent Rayleigh–Bénard convection

Published online by Cambridge University Press:  13 February 2018

Yin Wang ,
Wei Xu ,
Xiaozhou He ,
Hiufai Yik ,
Xiaoping Wang ,
Jörg Schumacher Open the ORCID record for Jörg Schumacher [Opens in a new window]  and
Penger Tong Open the ORCID record for Penger Tong [Opens in a new window]
Yin Wang
Affiliation:
Department of Physics, Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong
Wei Xu
Affiliation:
Nano Science and Technology Program, Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong
Xiaozhou He
Affiliation:
Institute for Turbulence-Noise-Vibration Interaction and Control, Shenzhen Graduate School, Harbin Institute of Technology, Shenzhen, China
Hiufai Yik
Affiliation:
Department of Physics, Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong
Xiaoping Wang
Affiliation:
Department of Mathematics, Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong
Jörg Schumacher
Affiliation:
Institut für Thermo- und Fluiddynamik, Postfach 100565, Technische Universität Ilmenau, D-98684 Ilmenau, Germany
Penger Tong*
Affiliation:
Department of Physics, Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We report a combined experimental and numerical study of the effect of boundary layer (BL) fluctuations on the scaling properties of the mean temperature profile 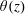$\unicode[STIX]{x1D703}(z)$ and temperature variance profile 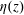$\unicode[STIX]{x1D702}(z)$ in turbulent Rayleigh–Bénard convection in a thin disk cell and an upright cylinder of aspect ratio unity. Two scaling regions are found with increasing distance $z$ away from the bottom conducting plate. In the BL region, the measured 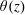$\unicode[STIX]{x1D703}(z)$ and 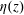$\unicode[STIX]{x1D702}(z)$ are found to have the scaling forms 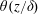$\unicode[STIX]{x1D703}(z/\unicode[STIX]{x1D6FF})$ and 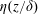$\unicode[STIX]{x1D702}(z/\unicode[STIX]{x1D6FF})$, respectively, with varying thermal BL thickness 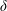$\unicode[STIX]{x1D6FF}$. The functional forms of the measured 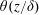$\unicode[STIX]{x1D703}(z/\unicode[STIX]{x1D6FF})$ and $\unicode[STIX]{x1D702}(z/\unicode[STIX]{x1D6FF})$ in the two convection cells agree well with the recently derived BL equations by Shishkina et al. (Phys. Rev. Lett., vol. 114, 2015, 114302) and by Wang et al. (Phys. Rev. Fluids, vol. 1, 2016, 082301). In the mixing zone outside the BL region, the measured 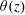$\unicode[STIX]{x1D703}(z)$ remains approximately constant, whereas the measured 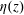$\unicode[STIX]{x1D702}(z)$ is found to scale with the cell height $H$ in the two convection cells and follows a power law, 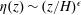$\unicode[STIX]{x1D702}(z)\sim (z/H)^{\unicode[STIX]{x1D716}}$, with the obtained values of $\unicode[STIX]{x1D716}$ being close to 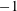$-1$. Based on the experimental and numerical findings, we derive a new equation for 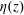$\unicode[STIX]{x1D702}(z)$ in the mixing zone, which has a power-law solution in good agreement with the experimental and numerical results. Our work demonstrates that the effect of BL fluctuations can be adequately described by the velocity–temperature correlation functions and the new BL equations capture the essential physics.

JFM classification

Boundary Layers: Boundary layer structure Turbulent Flows: Turbulence modelling
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 840 , 10 April 2018 , pp. 408 - 431
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J. 1996 Variation of temperature and velocity fluctuations in turbulent thermal convection over horizontal surfaces. Intl J. Heat Mass Transfer 39, 2303–2310.CrossRefGoogle Scholar
Ahlers, G., Brown, E. & Nikolaenko, A. 2006 Search for slow transients, and the effect of imperfect vertical alignment, in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 557, 347–367.Google Scholar
Ahlers, G., Brown, E., Araujo, F. F., Funfschilling, D., Grossmann, S. & Lohse, D. 2006 Non-Oberbeck–Boussinesq effects in strongly turbulent Rayleigh–Bénard convection. J. Fluid Mech. 569, 409–445.Google Scholar
Ahlers, G., Grossmann, S. & Lohse, D. 2009 Heat transfer and large scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81, 503–537.Google Scholar
Anderson, J. D. 2005 Ludwig Prandtl’s boundary layer. Phys. Today 58, 42–48.CrossRefGoogle Scholar
Belmonte, A., Tilgner, A. & Libchaber, A. 1993 Boundary layer length scales in thermal turbulence. Phys. Rev. Lett. 70, 4067–4070.CrossRefGoogle ScholarPubMed
Belmonte, A., Tilgner, A. & Libchaber, A. 1994 Temperature and velocity boundary layers in turbulent convection. Phys. Rev. E 50, 269–279.Google Scholar
Castaing, B., Gunaratne, G., Heslot, F., Kadanoff, L., Libchaber, A., Thomae, S., Wu, X.-Z., Zaleski, S. & Zanetti, G. 1988 Scaling of hard thermal turbulence in Rayleigh–Bénard convection. J. Fluid Mech. 204, 1–30.Google Scholar
Ching, E. S. C., Dung, O.-Y. & Shishkina, O. 2017 Fluctuating thermal boundary layers and heat transfer in turbulent Rayleigh–Bénard convection. J. Stat. Phys. 167, 626–635.Google Scholar
Deville, M. O., Fischer, P. F. & Mund, E. H. 2002 High-order Methods for Incompressible Fluid Flow. Cambridge University Press.Google Scholar
Du Puits, R., Resagk, C. & Thess, A. 2013 Thermal boundary layers in turbulent Rayleigh–Bénard convection at aspect ratios between 1 and 9. New J. Phys. 15 (1), 013040.Google Scholar
Du, Y.-B. & Tong, P. 2000 Turbulent thermal convection in a cell with ordered rough boundaries. J. Fluid Mech. 407, 57–84.CrossRefGoogle Scholar
Fischer, P. F. 1997 An overlapping Schwarz method for spectral element solution of the incompressible Navier–Stokes equations. J. Comput. Phys. 133, 84–101.Google Scholar
Grossmann, S. & Lohse, D. 2011 Multiple scaling in the ultimate regime of thermal convection. Phys. Fluids 23, 045108.Google Scholar
Grötzbach, G. 1983 Spatial resolution requirements for direct numerical simulation of the Rayleigh–Bénard convection. J. Comput. Phys. 49 (2), 241–264.CrossRefGoogle Scholar
He, X., Ching, E. S. C. & Tong, P. 2011 Locally averaged thermal dissipation rate in turbulent thermal convection: a decomposition into contributions from different temperature gradient components. Phys. Fluids 23, 025106.Google Scholar
He, X. & Tong, P. 2009 Measurements of the thermal dissipation field in turbulent Rayleigh–Bénard convection. Phys. Rev. E 79, 026306.Google Scholar
Kadanoff, L. P. 2001 Turbulent heat flow: structures and scaling. Phys. Today 54, 34–39.CrossRefGoogle Scholar
Kraichnan, R. H. 1962 Turbulent thermal convection at arbritrary Prandtl number. Phys. Fluids 5, 1374–1389.Google Scholar
Landau, L. D. & Lifshitz, E. M. 1987 Fluid Mechanics, 2nd edn. Pergamon Press.Google Scholar
Lui, S.-L. & Xia, K.-Q. 1998 Spatial structure of the thermal boundary layer in turbulent convection. Phys. Rev. E 57, 5494–5503.Google Scholar
Prandtl, L. 1904 Verhandlungen des dritten Internationalen Mathematiker-Kongresses in Heidelberg (ed. Krazer, A.), Teubner (1905), p. 484. English trans. in Early Developments of Modern Aerodynamics (ed. J. A. K. Ackroyd, B. P. Axcell & A. I. Ruban), Butterworth-Heinemann, Oxford, UK (2001), p. 77.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.CrossRefGoogle Scholar
Qiu, X.-L. & Tong, P. 2001 Large-scale velocity structures in turbulent thermal convection. Phys. Rev. E 64, 036304.Google Scholar
Scheel, J. D., Emran, M. S. & Schumacher, J. 2013 Resolving the fine-scale structure in turbulent Rayleigh–Bénard convection. New J. Phys. 15, 113063.CrossRefGoogle Scholar
Scheel, J. D., Kim, E. & White, K. R. 2012 Thermal and viscous boundary layers in turbulent Rayleigh–Bénard convection.. J. Fluid Mech. 711, 281–305.Google Scholar
Scheel, J. D. & Schumacher, J. 2014 Local boundary layer scales in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 758, 344–373.Google Scholar
Schlichting, H. & Gersten, K. 2000 Boundary Layer Theory, 8th edn. Springer.Google Scholar
Schumacher, J., Götzfried, P. & Scheel, J. D. 2015 Enhanced enstrophy generation for turbulent convection in low-Prandtl number fluids. Proc. Natl Acad. Sci. USA 112, 9535.Google Scholar
Shi, N., Emran, M. S. & Schumacher, J. 2012 Boundary layer structure in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 706, 5–33.Google Scholar
Shishkina, O. & Thess, A. 2009 Mean temperature profiles in turbulent Rayleigh–Bénard convection of water. J. Fluid Mech. 633, 449–460.Google Scholar
Shishkina, O., Horn, S. & Wagner, S. 2013 Falkner–Skan boundary layer approximation in Rayleigh–Bénard convection. J. Fluid Mech. 730, 442–463.Google Scholar
Shishkina, O., Horn, S., Wagner, S. & Ching, E. S. C. 2015 Thermal boundary layer equation for turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 114, 114302.Google Scholar
Shishkina, O., Horn, S., Wagner, S. & Ching, E. S. C. 2017 Mean temperature profiles in turbulent thermal convection. Phys. Rev. Fluids 2, 113502.Google Scholar
Shraiman, B. I. & Siggia, E. D. 1990 Heat transport in high-Rayleigh-number convection. Phys. Rev. A 42, 3650-6-3653.CrossRefGoogle ScholarPubMed
Song, H., Villermaux, E. & Tong, P. 2011 Coherent oscillations of turbulent Rayleigh–Bénard convection in a thin vertical disk. Phys. Rev. Lett. 106, 184504.Google Scholar
Song, H., Brown, E., Hawkins, R. & Tong, P. 2014 Dynamics of large-scale circulation of turbulent thermal convection in a horizontal cylinder. J. Fluid Mech. 740, 136–167.Google Scholar
Spiegel, E. A. 1971 Convection in stars. Ann. Rev. Astron. Astrophys. 9, 323–352.Google Scholar
Stevens, R. J. A. M., Lohse, D. & Verzicco, R. 2011 Prandtl and Rayleigh number dependence of heat transport in high Rayleigh number thermal convection. J. Fluid Mech. 688, 31–43.Google Scholar
Stevens, R. J. A. M., Zhou, Q., Grossmann, S., Verzicco, R., Xia, K.-Q. & Lohse, D. 2012 Thermal boundary layer profiles in turbulent Rayleigh–Bénard convection in a cylindrical sample. Phys. Rev. E 85, 027301.Google Scholar
Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. MIT Press.Google Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow, vol. 2. Cambridge University Press.Google Scholar
Wang, J. & Xia, K.-Q. 2003 Spatial variations of the mean and statistical quantities in the thermal boundary layers of turbulent convection. Eur. Phys. J. B 32, 127–136.Google Scholar
Wang, Y., He, X.-Z. & Tong, P. 2016 Boundary layer fluctuations and their effects on mean and variance temperature profiles in turbulent Rayleigh–Bénard convection. Phys. Rev. Fluids 1, 082301.Google Scholar
Wang, Y.2017 Fluctuations in turbulent Rayleigh–Bénard convection: from boundary layers to large-scale flows. PhD thesis, HKUST.Google Scholar
Wei, P. & Ahlers, G. 2016 On the nature of fluctuations in turbulent Rayleigh–Bénard convection at large Prandtl numbers. J. Fluid Mech. 802, 203–244.Google Scholar
Wu, X. Z. & Libchaber, A. 1991 Non-Boussinesq effects in free thermal convection. Phys. Rev. A 43, 2833–2839.Google Scholar
Zhang, J., Childress, S. & Libchaber, A. 1997 Non-Boussinesq effect: thermal convection with broken symmetry. Phys. Fluids 9, 1034–1042.Google Scholar
Zhou, Q. & Xia, K.-Q. 2013 Thermal boundary layer structure in turbulent Rayleigh–Bénard convection in a rectangular cell. J. Fluid Mech. 721, 199–224.Google Scholar