Hostname: page-component-599cfd5f84-ncv4z Total loading time: 0 Render date: 2025-01-07T08:15:44.789Z Has data issue: false hasContentIssue false
  • English
  • Français

Boundary conditions for free surface inlet and outlet problems

Published online by Cambridge University Press:  10 August 2012

M. Taroni ,
C. J. W. Breward ,
P. D. Howell  and
J. M. Oliver
M. Taroni*
Affiliation:
Mathematical Institute, University of Oxford, 24–29 St Giles, Oxford OX1 3LB, UK
C. J. W. Breward
Affiliation:
Mathematical Institute, University of Oxford, 24–29 St Giles, Oxford OX1 3LB, UK
P. D. Howell
Affiliation:
Mathematical Institute, University of Oxford, 24–29 St Giles, Oxford OX1 3LB, UK
J. M. Oliver
Affiliation:
Mathematical Institute, University of Oxford, 24–29 St Giles, Oxford OX1 3LB, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

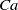We investigate and compare the boundary conditions that are to be applied to free-surface problems involving inlet and outlets of Newtonian fluid, typically found in coating processes. The flux of fluid is a priori known at an inlet, but unknown at an outlet, where it is governed by the local behaviour near the film-forming meniscus. In the limit of vanishing capillary number it is well known that the flux scales with 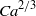, but this classical result is non-uniform as the contact angle approaches 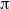. By examining this limit we find a solution that is uniformly valid for all contact angles. Furthermore, by considering the far-field behaviour of the free surface we show that there exists a critical capillary number above which the problem at an inlet becomes over-determined. The implications of this result for the modelling of coating flows are discussed.

JFM classification

Interfacial Flows (free surface): Capillary flows Low-Reynolds-number flows: Lubrication theory Interfacial Flows (free surface): Thin films
Type
Papers
Information
Journal of Fluid Mechanics , Volume 708 , 10 October 2012 , pp. 100 - 110
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Bretherton, F. P. 1961 The motion of long bubbles in tubes. J. Fluid Mech. 10, 166–188.CrossRefGoogle Scholar
2. Campana, D. M., Ubal, S., Giavedoni, M. D. & Saita, F. A. 2007 Stability of the steady motion of a liquid plug in a capillary tube. Ind. Engng Chem. Res. 46, 1803–1809.Google Scholar
3. Carou, J. Q., Wilson, S. K., Mottram, N. J. & Duffy, B. R. 2009 Asymptotic and numerical analysis of a simple model for blade coating. J. Engng Maths 63, 155–176.CrossRefGoogle Scholar
4. Christodoulou, K. N., Kistler, S. F. & Schunk, P. R. 1997 Advances in computational methods for free surface flows. In Liquid Film Coating. Scientific Principles and their Technological Implications (ed. Kistler, S. F. & Schweizer, P. M. ), pp. 297–366. Chapman & Hall.Google Scholar
5. Coyle, D. J., Macosko, C. W. & Scriven, L. E. 1990 The fluid dynamics of reverse roll coating. AIChE J. 36 (2), 161–174.CrossRefGoogle Scholar
6. Coyne, J. C. & Elrod, H. G. 1970 Conditions for the rupture of a lubrication film. Part 1. Theoretical model. Trans. ASME: J. Lubr. Technol. 92, 451.Google Scholar
7. Dowson, D. & Taylor, C. M. 1979 Cavitation in bearings. Annu. Rev. Fluid Mech. 11, 35–66.CrossRefGoogle Scholar
8. Dussan V., E. B. & Davis, S. H. 1974 On the motion of a fluid–fluid interface along a solid surface. J. Fluid Mech. 65, 71–95.CrossRefGoogle Scholar
9. Fujioka, H. & Grotberg, J. B. 2004 Steady propagation of a liquid plug in a two-dimensional channel. Trans. ASME: J. Biomech. Engng 126, 567–577.Google Scholar
10. Gaskell, P. H., Savage, M. D., Summers, J. L. & Thompson, H. M. 1995 Modelling and analysis of meniscus roll coating. J. Fluid Mech. 298, 113–137.CrossRefGoogle Scholar
11. Giavedoni, M. D. & Saita, F. A. 1997 The axisymmetric and plane cases of a gas phase steadily displacing a Newtonian liquid – a simultaneous solution of the governing equations. Phys. Fluids 19, 2420–2428.CrossRefGoogle Scholar
12. Giavedoni, M. D. & Saita, F. A. 1999 The rear meniscus of a long bubble steadily displacing a Newtonian liquid in a capillary tube. Phys. Fluids 11, 786–794.CrossRefGoogle Scholar
13. Hewson, R. W. 2009 Free surface model derived from the analytical solution of Stokes flow in a wedge. J. Fluid Engng 131, 041205.CrossRefGoogle Scholar
14. Hewson, R. W., Kapur, N. & Gaskell, P. H. 2009 A model for film-forming with Newtonian and shear-thinning fluids. J. Non-Newtonian Fluid Mech. 162, 21–28.CrossRefGoogle Scholar
15. Hocking, L. M. 1977 A moving fluid interface. Part 2. The removal of the force singularity by a slip flow. J. Fluid Mech. 79 (2), 209–229.CrossRefGoogle Scholar
16. Landau, L. D. & Levich, B. 1942 Dragging of a liquid by a moving plate. Acta Physicochim. 17, 42–54.Google Scholar
17. Moriarty, J. A. & Terrill, E. L. 1996 Mathematical modelling of the motion of hard contact lenses. Eur. J. Appl. Maths 7, 575–594.Google Scholar
18. Ockendon, J. R. & Ockendon, H. 1995 Viscous Flow. Cambridge University Press.CrossRefGoogle Scholar
19. Park, C.-W. & Homsy, G. M. 1984 Two-phase displacement in Hele-Shaw cells: theory. J. Fluid Mech. 139, 291–308.CrossRefGoogle Scholar
20. Reinelt, D. A. & Saffman, P. G. 1985 The penetration of a finger into a viscous fluid in a channel and tube. SIAM J. Sci. Stat. Comput. 6 (3), 542–561.CrossRefGoogle Scholar
21. Reynolds, O. 1886 On the theory of lubrication and its application to Beauchamp Tower’s experiments, including an experimental determination of the viscosity of olive oil. Phil. Trans. R. Soc. Lond. A 177, 157–233.Google Scholar
22. Ruschak, K. J. 1980 A method for incorporating free boundaries with surface tension in finite element fluid flow simulators. Int. J. Numer. Meth. Engng 15 (5), 639–648.CrossRefGoogle Scholar
23. Ruschak, K. J. 1982 Boundary conditions at a liquid/air interface in lubrication flows. J. Fluid Mech. 119, 107–120.CrossRefGoogle Scholar
24. Savage, M. D. 1977 Cavitation in lubrication. Part 1. On boundary conditions and cavity–fluid interfaces. J. Fluid Mech. 80, 743–755.CrossRefGoogle Scholar
25. Savage, M. D. 1982 Mathematical models for coating processes. J. Fluid Mech. 117, 443–455.CrossRefGoogle Scholar
26. Taroni, M., Breward, C. J. W., Howell, P. D., Oliver, J. M. & Young, R. J. S. 2012 The screen printing of a power-law fluid. J. Engng Maths 73, 93–119.CrossRefGoogle Scholar
27. Taylor, G. I. 1963 Cavitation of a viscous fluid in narrow passages. J. Fluid Mech. 16, 595–619.CrossRefGoogle Scholar
28. Weinstein, S. J. & Ruschak, K. J. 2004 Coating flows. Annu. Rev. Fluid Mech. 36, 29–53.CrossRefGoogle Scholar
29. Wilson, S. D. R. 1982 The drag-out problem in film coating theory. J. Engng Maths 16, 209–221.CrossRefGoogle Scholar
30. Wilson, S. D. R. & Jones, A. F. 1983 The entry of a falling film into a pool and the air-entrainment problem. J. Fluid Mech. 128, 219–230.CrossRefGoogle Scholar