Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-25T02:07:10.088Z Has data issue: false hasContentIssue false
  • English
  • Français

Bifurcations from steady to quasi-periodic flows in a laterally heated cavity filled with low Prandtl number fluids

Published online by Cambridge University Press:  21 December 2018

A. Medelfef Open the ORCID record for A. Medelfef [Opens in a new window] ,
D. Henry ,
A. Bouabdallah  and
S. Kaddeche
A. Medelfef*
Affiliation:
Laboratoire de Thermodynamique et Systèmes Energétiques, Faculté de Physique, Université des Sciences et de la Technologie Houari Boumediene – USTHB, BP 32, 16111 Bab Ezzouar, Alger, Algérie Laboratoire de Mécanique des Fluides et d’Acoustique, CNRS/Université de Lyon, Ecole Centrale de Lyon/Université Lyon 1/INSA Lyon – ECL, 36 avenue Guy de Collongue, 69134 Ecully CEDEX, France
D. Henry
Affiliation:
Laboratoire de Mécanique des Fluides et d’Acoustique, CNRS/Université de Lyon, Ecole Centrale de Lyon/Université Lyon 1/INSA Lyon – ECL, 36 avenue Guy de Collongue, 69134 Ecully CEDEX, France
A. Bouabdallah
Affiliation:
Laboratoire de Thermodynamique et Systèmes Energétiques, Faculté de Physique, Université des Sciences et de la Technologie Houari Boumediene – USTHB, BP 32, 16111 Bab Ezzouar, Alger, Algérie
S. Kaddeche
Affiliation:
Laboratoire de Recherche Matériaux, Mesures et Applications, Institut National des Sciences Appliquées et de Technologie – INSAT, B.P. 676, 1080 Tunis CEDEX, Tunisie
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This study deals with the transition toward quasi-periodicity of buoyant convection generated by a horizontal temperature gradient in a three-dimensional parallelepipedic cavity with dimensions 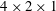$4\times 2\times 1$ (length $\times$ width $\times$ height). Numerical continuation techniques, coupled with an Arnoldi method, are used to locate the steady and Hopf bifurcation points as well as the different steady and periodic flow branches emerging from them for Prandtl numbers ranging from 0 to 0.025 (liquid metals). Our results highlight the existence of two steady states along with many periodic cycles, all with different symmetries. The bifurcation scenarios consist of complex paths between these different solutions, giving a succession of stable flow states as the Grashof number is increased, from steady to periodic and quasi-periodic. The change of these scenarios with the Prandtl number, in connection with the crossing of bifurcation points, was carefully analysed.

JFM classification

Nonlinear Dynamical Systems: Bifurcation Convection: Convection in cavities Instability: Nonlinear instability
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 861 , 25 February 2019 , pp. 223 - 252
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Afrid, M. & Zebib, A. 1990 Oscillatory three-dimensional convection in rectangular cavities and enclosures. Phys. Fluids 2 (8), 1318–1327.Google Scholar
Bacharoudis, E., Vrachopoulos, M. G., Koukou, M. K., Margaris, D., Filios, A. E. & Mavrommatis, S. A. 2007 Study of the natural convection phenomena inside a wall solar chimney with one wall adiabatic and one wall under a heat flux. Appl. Therm. Engng 27 (13), 2266–2275.Google Scholar
Ben Hadid, H. & Henry, D. 1997 Numerical study of convection in the horizontal Bridgman configuration under the action of a constant magnetic field. Part 2. Three dimensional flow. J. Fluid Mech. 333, 57–83.Google Scholar
Bergeon, A., Henry, D., Ben Hadid, H. & Tuckerman, L. S. 1998 Marangoni convection in binary mixtures with Soret effect. J. Fluid Mech. 375, 143–177.Google Scholar
Braunsfurth, M. G. & Mullin, T. 1996 An experimental study of oscillatory convection in liquid gallium. J. Fluid Mech. 327, 199–219.Google Scholar
Cormack, D. E., Leal, L. & Imberger, J. 1974a Natural convection in a shallow cavity with differentially heated end walls. Part 1. Asymptotic theory. J. Fluid Mech. 65 (2), 209–229.Google Scholar
Cormack, D. E., Leal, L. & Seinfeld, J. H. 1974b Natural convection in a shallow cavity with differentially heated end walls. Part 2. Numerical solutions. J. Fluid Mech. 65 (2), 231–246.Google Scholar
Daviaud, F. & Vince, J. M. 1993 Traveling waves in a fluid layer subjected to a horizontal temperature gradient. Phys. Rev. E 48, 4432–4436.Google Scholar
Dhanaraj, G., Byrappa, K., Prasad, V. & Dudley, M. 2010 Springer Handbook of Crystal Growth. Springer.Google Scholar
Dupont, S., Marchal, J. M., Crochet, M. & Geyling, F. T. 1987 Numerical simulation of the horizontal Bridgman growth. Part II. Three-dimensional flow. Intl J. Numer. Meth. Fluids 7 (1), 49–67.Google Scholar
Gershuni, G., Laure, P., Myznikov, V., Roux, B. & Zhukhovitsky, E. 1992 On the stability of plane-parallel advective flows in long horizontal layers. Microgravity Q. 2, 141–151.Google Scholar
Hart, J. E. 1972 Stability of thin non-rotating Hadley circulations. J. Atmos. Sci. 29, 687–696.Google Scholar
Henry, D. & Ben Hadid, H. 2007 Multiple flow transitions in a box heated from the side in low-Prandtl-number fluids. Phys. Rev. E 76, 016314.Google Scholar
Henry, D. & Buffat, M. 1998 Two- and three-dimensional numerical simulations of the transition to oscillatory convection in low-Prandtl-number fluids. J. Fluid Mech. 374, 145–171.Google Scholar
Hof, B., Juel, A., Zhao, L., Henry, D., Ben Hadid, H. & Mullin, T. 2004 On the onset of oscillatory convection in molten gallium. J. Fluid Mech. 515, 391–413.Google Scholar
Hung, M. C. & Andereck, C. D. 1988 Transitions in convection driven by a horizontal temperature gradient. Phys. Lett. A 132 (5), 253–258.Google Scholar
Hurle, D. T. J. 1966 Temperature oscillations in molten metals and their relationship to the growth state in melt grown crystals. Phil. Mag. 13, 305–310.Google Scholar
Hurle, D. T. J., Jakeman, E. & Johnson, C. P. 1974 Convective temperature oscillations in molten gallium. J. Fluid Mech. 64, 565–576.Google Scholar
Juel, A., Mullin, T., Ben Hadid, H. & Henry, D. 1999 Magnetohydrodynamic convection in molten gallium. J. Fluid Mech. 378, 97–118.Google Scholar
Juel, A., Mullin, T., Ben Hadid, H. & Henry, D. 2001 Three-dimensional free convection in molten gallium. J. Fluid Mech. 436, 267–281.Google Scholar
Karniadakis, G. E. 1991 High-order splitting methods for incompressible Navier–Stokes equations. J. Comput. Phys. 97, 414–443.Google Scholar
Klausmeier, C. A. 2008 Floquet theory: a useful tool for understanding nonequilibrium dynamics. Theor. Ecol. 1, 53–161.Google Scholar
Lappa, M. 2007 Secondary and oscillatory gravitational instabilities in canonical three-dimensional models of crystal growth from the melt. Part 2. Lateral heating and the Hadley circulation. Comptes Rendus Mécanique 335 (5), 261–268.Google Scholar
Laure, P. 1987 Étude des mouvements de convection dans une cavité rectangulaire soumise à un gradient de température horizontal. J. Theor. Appl. Mech. 6, 351–382.Google Scholar
Laure, P. & Roux, B. 1989 Linear and non-linear analysis of the Hadley circulation. J. Cryst. Growth 97, 226–234.Google Scholar
Lyubimova, T. P., Lyubimov, D. V., Morozov, V. A., Henry, D. & Ben Hadid, H. 2009b Stability of convection in a horizontal channel subjected to a longitudinal temperature gradient. Part 2. Effect of a magnetic field. J. Fluid Mech. 635, 297–319.Google Scholar
Lyubimova, T. P., Lyubimov, D. V., Morozov, V. A., Scuridin, R. V., Ben Hadid, H. & Henry, D. 2009a Stability of convection in a horizontal channel subjected to a longitudinal temperature gradient. Part 1. Effect of aspect ratio and Prandtl number. J. Fluid Mech. 635, 275–295.Google Scholar
Mamun, C. K. & Tuckerman, L. S. 1995 Asymmetry and Hopf bifurcation in spherical Couette flow. Phys. Fluids 7 (1), 80–91.Google Scholar
McKell, K. E., Broomhead, D. S., Jones, R. & Hurle, D. T. J. 1990 Torus doubling in convecting molten gallium. Europhys. Lett. 12 (6), 513–518.Google Scholar
Mercader, I., Batiste, O., Ramírez-Piscina, L., Ruiz, X., Rüdiger, S. & Casademunt, J. 2005 Bifurcations and chaos in single-roll natural convection with low Prandtl number. Phys. Fluids 17 (10), 104108.Google Scholar
Mohamad, A. A. & Viskanta, R. 1991 Transient natural convection of low-Prandtl-number fluids in a differentially heated cavity. Intl J. Numer. Meth. Fluids 13 (1), 61–81.Google Scholar
Pimputkar, S. M. & Ostrach, S. 1981 Convective effects in crystals grown from melts. J. Cryst. Growth 55, 614–646.Google Scholar
Puigjaner, D., Herrero, J., Simó, C. & Giralt, F. 2011 From steady solutions to chaotic flows in a Rayleigh–Bénard problem at moderate Rayleigh numbers. Physica D 240 (11), 920–934.Google Scholar
Pulicani, J. P., Arco, E. C. D., Randriamampianina, A., Bontoux, P. & Peyret, R. 1990 Spectral simulations of oscillatory convection at low Prandtl number. Intl J. Numer. Meth. Fluids 10 (5), 481–517.Google Scholar
Sánchez, J., Net, M., García-Archilla, B. & Simó, C. 2004 Newton–Krylov continuation of periodic orbits for Navier–Stokes flows. J. Comput. Phys. 201 (1), 13–33.Google Scholar
Seydel, R. 2010 Practical Bifurcation and Stability Analysis. Springer.Google Scholar
Torres, J. F., Henry, D., Komiya, A. & Maruyama, S. 2014 Bifurcation analysis of steady natural convection in a tilted cubical cavity with adiabatic sidewalls. J. Fluid Mech. 756, 650–688.Google Scholar
Torres, J. F., Henry, D., Komiya, A., Maruyama, S. & Ben Hadid, H. 2013 Three-dimensional continuation study of convection in a tilted rectangular enclosure. Phys. Rev. E 88, 043015.Google Scholar
Wakitani, S. 2000 Numerical study of three-dimensional oscillatory natural convection at low Prandtl number in rectangular enclosures. Trans. ASME J. Heat Transfer 123, 77–83.Google Scholar