Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-28T11:58:47.189Z Has data issue: false hasContentIssue false
  • English
  • Français

Bifurcation theory for vortices with application to boundary layer eruption

Published online by Cambridge University Press:  27 February 2019

Anne R. Nielsen Open the ORCID record for Anne R. Nielsen [Opens in a new window] ,
Matthias Heil Open the ORCID record for Matthias Heil [Opens in a new window] ,
Morten Andersen Open the ORCID record for Morten Andersen [Opens in a new window]  and
Morten Brøns Open the ORCID record for Morten Brøns [Opens in a new window]
Anne R. Nielsen
Affiliation:
Department of Applied Mathematics and Computer Science, Technical University of Denmark, 2800 Lyngby, Denmark
Matthias Heil
Affiliation:
School of Mathematics, University of Manchester, Oxford Road, Manchester M13 9PL, UK
Morten Andersen
Affiliation:
Department of Science and Environment, Roskilde University, 4000 Roskilde, Denmark
Morten Brøns*
Affiliation:
Department of Applied Mathematics and Computer Science, Technical University of Denmark, 2800 Lyngby, Denmark
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We develop a bifurcation theory describing the conditions under which vortices are created or destroyed in a two-dimensional incompressible flow. We define vortices using the 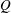$Q$-criterion and analyse the vortex structure by considering the evolution of the zero contours of 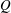$Q$. The theory identifies topological changes of the vortex structure and classifies these as four possible types of bifurcations, two occurring away from boundaries, and two occurring near no-slip walls. Our theory provides a description of all possible codimension-one bifurcations where time is treated as the bifurcation parameter. To illustrate our results, we consider the early stages of boundary layer eruption at moderate Reynolds numbers in the range from 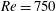$Re=750$ to 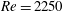$Re=2250$. By analysing numerical simulations of the phenomenon, we show how to describe the eruption process as sequences of the four possible bifurcations of codimension one. Our simulations show that there is a single codimension-two point within our parameter range. This codimension-two point arises at 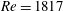$Re=1817$ via the coalescence of two codimension-one bifurcations which are associated with the creation and subsequent destruction of one of the vortices that erupt from the boundary layer. We present a theoretical description of this process and explain how the occurrence of this phenomenon separates the parameter space into two regions with distinct evolution of the topology of the vortices.

JFM classification

Boundary Layers: Boundary layer structure Mathematical Foundations: Topological fluid dynamics Vortex Flows: Vortex dynamics
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 865 , 25 April 2019 , pp. 831 - 849
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andersen, M.2013 Topology of streamlines and vorticity contours for two-dimensional flows. PhD thesis, Technical University of Denmark.Google Scholar
Balci, A., Andersen, M., Thompson, M. C. & Brøns, M. 2015 Codimension three bifurcation of streamline patterns close to a no-slip wall: a topological description of boundary layer eruption. Phys. Fluids 27 (5), 53603.10.1063/1.4921527Google Scholar
Brøns, M. 2007 Streamline topology: patterns in fluid flows and their bifurcations. Adv. Appl. Mech. 41, 1–42.10.1016/S0065-2156(07)41001-8Google Scholar
Brøns, M. & Bisgaard, A. 2006 Bifurcation of vortex breakdown patterns in a circular cylinder with two rotating covers. J. Fluid Mech. 568, 329–349.10.1017/S0022112006002424Google Scholar
Chakraborty, P., Balachandar, S. & Adrian, R. J. 2005 On the relationships between local vortex identification schemes. J. Fluid Mech. 535, 189–214.10.1017/S0022112005004726Google Scholar
Chen, Q., Zhong, Q., Qi, M. & Wang, X. 2015 Comparison of vortex identification criteria for planar velocity fields in wall turbulence. Phys. Fluids 27 (8), 085101.10.1063/1.4927647Google Scholar
Doligalski, T. L. & Walker, J. D. A. 1984 The boundary layer induced by a convected two-dimensional vortex. J. Fluid Mech. 139, 1–28.Google Scholar
Elsas, J. H. & Moriconi, L. 2017 Vortex identification from local properties of the vorticity field. Phys. Fluids 29 (1), 015101.10.1063/1.4973243Google Scholar
Haller, G., Hadjighasem, A., Farazmand, M. & Huhn, F. 2016 Defining coherent vortices objectively from the vorticity. J. Fluid Mech. 795, 136–173.10.1017/jfm.2016.151Google Scholar
Heil, M. & Hazel, A. L. 2006 oomph-lib – an object-oriented multi-physics finite-element library. In Fluid–Structure Interaction, Lecture Notes in Computational Science and Engineering, vol. 53, pp. 19–49. Springer.10.1007/3-540-34596-5_2Google Scholar
Heil, M., Rosso, J., Hazel, A. L. & Brøns, M. 2017 Topological fluid mechanics of the formation of the Kármán-vortex street. J. Fluid Mech. 812, 199–221.Google Scholar
Hörmander, L. 2007 The Analysis of Linear Partial Differential Operators III. Springer.Google Scholar
Hunt, J. C. R, Wray, A. A. & Moin, P.1988 Eddies, streams, and convergence zones in turbulent flows. Tech. Rep. CTR-S88. Center for Turbulence Research, Stanford University.Google Scholar
Jeong, J & Hussain, F 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.Google Scholar
Kudela, H. & Malecha, Z. M. 2009 Eruption of a boundary layer induced by a 2D vortex patch. Fluid Dyn. Res. 41 (5), 055502.10.1088/0169-5983/41/5/055502Google Scholar
Obabko, A. V. & Cassel, K. W. 2002 Navier–Stokes solutions of unsteady separation induced by a vortex. J. Fluid Mech. 465, 99–130.Google Scholar
Robinson, S. K. 1991 Coherent motions in the turbulent boundary-layer. Annu. Rev. Fluid Mech. 23 (1), 601–639.10.1146/annurev.fl.23.010191.003125Google Scholar
Wiggins, S. 2003 Introduction to Applied Nonlinear Dynamical Systems and Chaos. Springer.Google Scholar
Williams, J. C. 1977 Incompressible boundary-layer separation. Annu. Rev. Fluid Mech. 9 (1), 113–144.10.1146/annurev.fl.09.010177.000553Google Scholar
Zhang, Y., Liu, K., Xian, H. & Du, X. 2018 A review of methods for vortex identification in hydroturbines. Renew. Sustain. Energy Rev. 81, 1269–1285.10.1016/j.rser.2017.05.058Google Scholar
Zhong, Q., Chen, Q., Chen, H. & Li, D. 2017 A topological method for vortex identification in turbulent flows. Fluid Dyn. Res. 49 (1), 015509.10.1088/1873-7005/49/1/015509Google Scholar
Zhou, J., Adrian, R. J., Balachandar, S. & Kendall, T. M. 1999 Mechanisms for generating coherent packets of hairpin vortices in channel flow. J. Fluid Mech. 387, 353–396.Google Scholar