Hostname: page-component-599cfd5f84-96rnj Total loading time: 0 Render date: 2025-01-07T08:01:26.607Z Has data issue: false hasContentIssue false
  • English
  • Français

Bifurcating flows of plunging aerofoils at high Strouhal numbers

Published online by Cambridge University Press:  08 August 2012

D. J. Cleaver ,
Z. Wang  and
I. Gursul
D. J. Cleaver
Affiliation:
Department of Mechanical Engineering, University of Bath, Bath BA2 7AY, UK
Z. Wang
Affiliation:
Department of Mechanical Engineering, University of Bath, Bath BA2 7AY, UK
I. Gursul*
Affiliation:
Department of Mechanical Engineering, University of Bath, Bath BA2 7AY, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

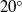Force and particle image velocimetry measurements were conducted on a NACA 0012 aerofoil undergoing small-amplitude high-frequency plunging oscillation at low Reynolds numbers and angles of attack in the range 0–. For angles of attack less than or equal to the stall angle, at high Strouhal numbers, significant bifurcations are observed in the time-averaged lift coefficient resulting in two lift-coefficient branches. The upper branch is associated with an upwards deflected jet, and the lower branch is associated with a downwards deflected jet. These branches are stable and highly repeatable, and are achieved by increasing or decreasing the frequency in the experiments. Increasing frequency refers to starting from stationary and increasing the frequency very slowly (while waiting for the flow to reach an asymptotic state after each change in frequency); decreasing frequency refers to impulsively starting at the maximum frequency and decreasing the frequency very slowly. For the latter case, angle of attack, starting position and initial acceleration rate are also parameters in determining which branch is selected. The bifurcation behaviour is closely related to the properties of the trailing-edge vortices. The bifurcation was therefore not observed for very small plunge amplitudes or frequencies due to insufficient trailing-edge vortex strength, nor at larger angles of attack due to greater asymmetry in the strength of the trailing-edge vortices, which creates a preference for a downward deflected jet. Vortex strength and asymmetry parameters are derived from the circulation measurements. It is shown that the most appropriate strength parameter in determining the onset of deflected jets is the circulation normalized by the plunge velocity.

JFM classification

Nonlinear Dynamical Systems: Bifurcation Wakes/Jets: Vortex streets
Type
Papers
Information
Journal of Fluid Mechanics , Volume 708 , 10 October 2012 , pp. 349 - 376
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Bohl, D. G. & Koochesfahani, M. M. 2009 MTV measurements of the vortical field in the wake of an airfoil oscillating at high reduced frequency. J. Fluid Mech. 620, 63–88.CrossRefGoogle Scholar
2. Bratt, J. B. 1950 Flow patterns in the wake of an oscillating airfoil. Aero. Res. Counc. R&M 2773.Google Scholar
3. Cleaver, D. J., Wang, Z. J. & Gursul, I. 2009 a Delay of stall by small amplitude airfoil oscillation at low Reynolds numbers. AIAA Paper 2009-392.CrossRefGoogle Scholar
4. Cleaver, D. J., Wang, Z. J. & Gursul, I. 2009 b Lift enhancement on oscillating airfoils. AIAA Paper 2009-4028.Google Scholar
5. Cleaver, D. J., Wang, Z. & Gursul, I. 2010 Vortex mode bifurcation and lift force of a plunging airfoil at low Reynolds numbers. AIAA Paper 2010-390.Google Scholar
6. Cleaver, D. J., Wang, Z. & Gursul, I. 2011 Lift enhancement by means of small amplitude airfoil oscillations at low Reynolds numbers. AIAA J. 49 (9), 2018–2033.Google Scholar
7. von Ellenrieder, K. D. & Pothos, S. 2008 PIV measurements of the asymmetric wake of a two-dimensional heaving hydrofoil. Exp. Fluids 44 (5), 733–745.CrossRefGoogle Scholar
8. Emblemsvag, J. E., Suzuki, R. & Candler, G. 2002 Numerical simulation of flapping micro air vehicles. AIAA Paper 2002-3197.CrossRefGoogle Scholar
9. Frampton, K. D., Goldfarb, M., Monopoli, D. & Cveticanin, D. 2002 Passive aeroelastic tailoring for optimal flapping wings. In Fixed and Flapping Wing Aerodynamics for Micro Air Vehicle Applications (ed. Mueller, T. J. ), pp. 473–482. AIAA.Google Scholar
10. Godoy-Diana, R., Aider, J. L. & Wesfreid, J. E. 2008 Transitions in the wake of a flapping foil. Phys. Rev. E 77, 1.Google Scholar
11. Godoy-Diana, R., Marais, C., Aider, J. L. & Wesfreid, J. E. 2009 A model for the symmetry breaking of the reverse Benard–von Kármán vortex street produced by a flapping foil. J. Fluid Mech. 622, 23–32.Google Scholar
12. Graftieaux, L., Michard, M. & Grosjean, N. 2001 Combining PIV, POD and vortex identification algorithms for the study of unsteady turbulent swirling flows. Meas. Sci. Technol. 12 (9), 1422–1429.Google Scholar
13. Heathcote, S. & Gursul, I. 2007a Flexible flapping airfoil propulsion at low Reynolds numbers. AIAA J. 45 (5), 1066–1079.Google Scholar
14. Heathcote, S. & Gursul, I. 2007b Jet switching phenomenon for a periodically plunging airfoil. Phys. Fluids 19, 2.Google Scholar
15. Ho, S., Nassef, H., Pornsinsirirak, N., Tai, Y. C. & Ho, C. M. 2003 Unsteady aerodynamics and flow control for flapping wing flyers. Prog. Aerosp. Sci. 39 (8), 635–681.CrossRefGoogle Scholar
16. Jones, K. D., Dohring, C. M. & Platzer, M. F. 1998 Experimental and computational investigation of the Knoller–Betz effect. AIAA J. 36 (7), 1240–1246.CrossRefGoogle Scholar
17. Lewin, G. C. & Haj-Hariri, H. 2003 Modelling thrust generation of a two-dimensional heaving airfoil in a viscous flow. J. Fluid Mech. 492, 339–362.CrossRefGoogle Scholar
18. Liang, C. L., Ou, K., Premasuthan, S., Jameson, A. & Wang, Z. J. 2011 High-order accurate simulations of unsteady flow past plunging and pitching airfoils. Comput. Fluids 40 (1), 236–248.Google Scholar
19. Milne-Thomson, L. M. 1968 Theoretical Hydrodynamics. Macmillan.Google Scholar
20. Moffat, R. J. 1988 Describing the uncertainties in experimental results. Exp. Therm. Fluid Sci. 1 (1), 3–17.Google Scholar
21. Morgan, C. E., Babinsky, H. & Harvey, J. K. 2009 Vortex detection methods for use with PIV and CFD data. AIAA Paper 2009-74.Google Scholar
22. Platzer, M. F., Jones, K. D., Young, J. & Lai, J. C. S. 2008 Flapping-wing aerodynamics: progress and challenges. AIAA J. 46 (9), 2136–2149.Google Scholar
23. Sane, S. P. 2003 The aerodynamics of insect flight. J. Expl Biol. 206 (23), 4191–4208.Google Scholar
24. Shyy, W., Berg, M. & Ljungqvist, D. 1999 Flapping and flexible wings for biological and micro air vehicles. Prog. Aerosp. Sci. 35 (5), 455–505.Google Scholar
25. Triantafyllou, M. S., Triantafyllou, G. S. & Yue, D. K. P. 2000 Hydrodynamics of fishlike swimming. Annu. Rev. Fluid Mech. 32, 33–53.CrossRefGoogle Scholar
26. Visbal, M. R. 2009 High-fidelity simulation of transitional flows past a plunging airfoil. AIAA J. 47 (11), 2685–2697.Google Scholar
27. Wang, Z. J. 2000 Two-dimensional mechanism for insect hovering. Phys. Rev. Lett. 85 (10), 2216–2219.CrossRefGoogle Scholar