Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Varade, Vijay
Agrawal, Amit
and
Pradeep, A. M.
2014.
Experimental study of rarefied gas flow near sudden contraction junction of a tube.
Physics of Fluids,
Vol. 26,
Issue. 6,
Singh, Narendra
and
Agrawal, Amit
2014.
The Burnett equations in cylindrical coordinates and their solution for flow in a microtube.
Journal of Fluid Mechanics,
Vol. 751,
Issue. ,
p.
121.
Varade, Vijay
Agrawal, Amit
Prabhu, S.V.
and
Pradeep, A.M.
2015.
Early onset of flow separation with rarefied gas flowing in a 90° bend tube.
Experimental Thermal and Fluid Science,
Vol. 66,
Issue. ,
p.
221.
Varade, Vijay
Agrawal, Amit
Prabhu, S.V.
and
Pradeep, A.M.
2015.
Velocity measurement in low Reynolds and low Mach number slip flow through a tube.
Experimental Thermal and Fluid Science,
Vol. 60,
Issue. ,
p.
284.
Varade, Vijay
Duryodhan, V.S.
Agrawal, Amit
Pradeep, A.M.
Ebrahimi, Amin
and
Roohi, Ehsan
2015.
Low Mach number slip flow through diverging microchannel.
Computers & Fluids,
Vol. 111,
Issue. ,
p.
46.
Varade, Vijay
Agrawal, Amit
and
Pradeep, A M
2015.
Slip flow through a converging microchannel: experiments and 3D simulations.
Journal of Micromechanics and Microengineering,
Vol. 25,
Issue. 2,
p.
025015.
Mahdavi, Amir-Mehran
and
Roohi, Ehsan
2015.
Investigation of cold-to-hot transfer and thermal separation zone through nano step geometries.
Physics of Fluids,
Vol. 27,
Issue. 7,
Hemadri, Vadiraj
Varade, Vijay V.
Agrawal, Amit
and
Bhandarkar, U. V.
2016.
Investigation of rarefied gas flow in microchannels of non-uniform cross section.
Physics of Fluids,
Vol. 28,
Issue. 2,
Gavasane, Abhimanyu
Agrawal, Amit
Pradeep, A. M.
and
Bhandarkar, Upendra
2017.
Simulation of a temperature drop for the flow of rarefied gases in microchannels.
Numerical Heat Transfer, Part A: Applications,
Vol. 71,
Issue. 10,
p.
1066.
Ebrahimi, Amin
and
Roohi, Ehsan
2017.
DSMC investigation of rarefied gas flow through diverging micro- and nanochannels.
Microfluidics and Nanofluidics,
Vol. 21,
Issue. 2,
Hemadri, Vadiraj
Varade, Vijay V.
Agrawal, Amit
and
Bhandarkar, U. V.
2017.
Rarefied gas flow in converging microchannel in slip and early transition regimes.
Physics of Fluids,
Vol. 29,
Issue. 3,
Gavasane, Abhimanyu
Agrawal, Amit
and
Bhandarkar, Upendra
2018.
Study of rarefied gas flows in backward facing micro-step using Direct Simulation Monte Carlo.
Vacuum,
Vol. 155,
Issue. ,
p.
249.
Hammad, Khaled J.
2018.
Heat transfer enhancement in suddenly expanding annular shear-thinning flows.
International Journal of Heat and Mass Transfer,
Vol. 121,
Issue. ,
p.
28.
Taassob, Arsalan
Kamali, Reza
and
Bordbar, Alireza
2018.
Investigation of rarefied gas flow through bended microchannels.
Vacuum,
Vol. 151,
Issue. ,
p.
197.
Hemadri, Vadiraj
Duryodhan, V. S.
and
Agrawal, Amit
2018.
Liquid and gas flows in microchannels of varying cross section: a comparative analysis of the flow dynamics and design perspectives.
Microfluidics and Nanofluidics,
Vol. 22,
Issue. 2,
Sazhin, O.
2020.
Rarefied gas flow into vacuum through a channel with sudden contraction or expansion.
Microfluidics and Nanofluidics,
Vol. 24,
Issue. 10,
Garg, Richie
and
Agrawal, Amit
2020.
Poiseuille number behavior in an adiabatically choked microchannel in the slip regime.
Physics of Fluids,
Vol. 32,
Issue. 11,
Abedi Masir, M.
Aghaie, M.
and
Alahyarizadeh, Gh.
2020.
Simulation of separative gaseous molecular flow through porous membrane with DSMC method.
Progress in Nuclear Energy,
Vol. 118,
Issue. ,
p.
103150.
Agrawal, Amit
Kushwaha, Hari Mohan
and
Jadhav, Ravi Sudam
2020.
Microscale Flow and Heat Transfer.
p.
305.
Manela, A.
and
Gibelli, L.
2020.
Free-molecular and near-free-molecular gas flows over backward facing steps.
Journal of Fluid Mechanics,
Vol. 889,
Issue. ,
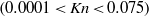 $(0. 0001\lt \mathit{Kn}\lt 0. 075)$ falls in the slip flow regime; the Reynolds number in the smaller section (
$(0. 0001\lt \mathit{Kn}\lt 0. 075)$ falls in the slip flow regime; the Reynolds number in the smaller section (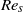 ${\mathit{Re}}_{s} $) ranges between 0.2 and 837. The static pressure along the wall is measured for different mass flow rates controlled by a mass flow controller and analysed to understand the flow behaviour. The velocity profiles are obtained through a momentum balance and using the pressure measurements. A discontinuity in the slope of pressure at the sudden expansion junction is noted and given special attention. The absence of flow separation is another key feature observed from the measurements. The streamlines are found to be concave near the junction. It is demonstrated that the flow ‘senses’ the oncoming sudden expansion junction and starts adjusting itself much before reaching the junction; this interesting behaviour is attributed to an increased axial momentum diffusion and wall slip. The additional acceleration of the central core of the gas flow causes an increase in the wall shear stress and a larger pressure drop as compared with a straight tube. These results are not previously available and should help in improving understanding of gaseous slip flows.
${\mathit{Re}}_{s} $) ranges between 0.2 and 837. The static pressure along the wall is measured for different mass flow rates controlled by a mass flow controller and analysed to understand the flow behaviour. The velocity profiles are obtained through a momentum balance and using the pressure measurements. A discontinuity in the slope of pressure at the sudden expansion junction is noted and given special attention. The absence of flow separation is another key feature observed from the measurements. The streamlines are found to be concave near the junction. It is demonstrated that the flow ‘senses’ the oncoming sudden expansion junction and starts adjusting itself much before reaching the junction; this interesting behaviour is attributed to an increased axial momentum diffusion and wall slip. The additional acceleration of the central core of the gas flow causes an increase in the wall shear stress and a larger pressure drop as compared with a straight tube. These results are not previously available and should help in improving understanding of gaseous slip flows.

