Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-12-02T21:48:46.008Z Has data issue: false hasContentIssue false
  • English
  • Français

Balanced solutions for an ellipsoidal vortex in a rotating stratified flow

Published online by Cambridge University Press:  03 August 2016

William J. McKiver  and
David G. Dritschel
William J. McKiver*
Affiliation:
ISMAR-CNR, Arsenale - Tesa 104, Castello 2737/F, 30122 Venice, Italy
David G. Dritschel
Affiliation:
School of Mathematics and Statistics, University of St Andrews, St Andrews KY16 9SS, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the motion of a single ellipsoidal vortex with uniform potential vorticity in a rotating stratified fluid at finite Rossby number $\unicode[STIX]{x1D716}$. Building on previous solutions obtained under the quasi-geostrophic approximation (at first order in $\unicode[STIX]{x1D716}$), we obtain analytical solutions for the balanced part of the flow at 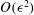$O(\unicode[STIX]{x1D716}^{2})$. These solutions capture important ageostrophic effects giving rise to an asymmetry in the evolution of cyclonic and anticyclonic vortices. Previous work has shown that, if the velocity field induced by an ellipsoidal vortex only depends linearly on spatial coordinates inside the vortex, i.e. 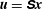$\boldsymbol{u}=\unicode[STIX]{x1D64E}\boldsymbol{x}$, then the dynamics reduces markedly to a simple matrix equation. The instantaneous vortex shape and orientation are encapsulated in a symmetric 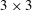$3\times 3$ matrix $\unicode[STIX]{x1D63D}$, which is acted upon by the flow matrix 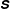$\unicode[STIX]{x1D64E}$ to provide the vortex evolution. Under the quasi-geostrophic approximation, the flow matrix is determined by inverting the potential vorticity to obtain the streamfunction via Poisson’s equation, which has a known analytical solution depending on elliptic integrals. Here we show that higher-order balanced solutions, up to second order in the Rossby number, can also be calculated analytically. However, in this case there is a vector potential that requires the solution of three Poisson equations for each of its components. The source terms for these equations are independent of spatial coordinates within the ellipsoid, depending only on the elliptic integrals solved at the leading, quasi-geostrophic order. Unlike the quasi-geostrophic case, these source terms do not in general vanish outside the ellipsoid and have an inordinately complicated dependence on spatial coordinates. In the special case of an ellipsoid whose axes are aligned with the coordinate axes, we are able to derive these source terms and obtain the full analytical solution to the three Poisson equations. However, if one considers the homogeneous case, whereby the outer source terms are neglected, one can obtain an approximate solution having a compact matrix form analogous to the leading-order quasi-geostrophic case. This approximate solution proves to be highly accurate for the general case of an arbitrarily oriented ellipsoid, as verified through comparisons of the solutions with solutions obtained from numerical simulations of an ellipsoid using an accurate nonlinear balance model, even at moderate Rossby numbers.

JFM classification

Geophysical and Geological Flows: Geophysical and Geological Flows Geophysical and Geological Flows: Geostrophic turbulence Vortex Flows: Vortex dynamics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 802 , 10 September 2016 , pp. 333 - 358
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baer, F. & Tribbia, J. J. 1977 On complete filtering of gravity modes through nonlinear initialization. Mon. Weath. Rev. 105, 1536–1539.2.0.CO;2>CrossRefGoogle Scholar
Bokhove, O. 1997 Slaving principles, balanced dynamics, and the hydrostatic Boussinesq equations. J. Atmos. Sci. 54, 1662–1674.Google Scholar
Bosse, A., Testor, P., Mortier, L., Prieur, L., Taillandier, V., d’Ortenzio, F. F. & Coppola, L. 2015 Spreading of Levantine intermediate waters by submesoscale coherent vortices in the northwestern Mediterranean Sea as observed with gliders. J. Geophys. Res. Oceans 120, 1599–1622.Google Scholar
Carlson, B. C. 1977 Special Functions of Applied Mathematics Academic.Google Scholar
Chandrasekhar, S. 1969 Ellipsoidal Figures of Equilibrium. Dover.Google Scholar
Charney, J. G. 1948 On the scale of atmospheric motions. Geofys. Publ. 17 (2), 3–17.Google Scholar
D’Asaro, E. 1988 Observations of small eddies in the Beaufort Sea. J. Geophys. Res. 93, 6669–6684.Google Scholar
Dassios, G. 2012 Ellipsoidal Harmonics: Theory and Applications. Cambridge University Press.Google Scholar
Dritschel, D. G. 1990 The stability of elliptical vortices in an external straining flow. J. Fluid Mech. 210, 223–261.Google Scholar
Dritschel, D. G. 1998 On the persistence of non-axisymmetric vortices in inviscid two-dimensional flows. J. Fluid Mech. 371, 141–155.Google Scholar
Dritschel, D. G. & McKiver, W. J. 2015 Effect of Prandtl’s ratio on balance in geophysical turbulence. J. Fluid Mech. 777, 569–590.CrossRefGoogle Scholar
Dritschel, D. G, Reinaud, J. N. & McKiver, W. J. 2004 The quasi-geostrophic ellipsoidal vortex model. J. Fluid Mech. 505, 201–223.Google Scholar
Dritschel, D. G., Scott, R. K. & Reinaud, J. N. 2005 The stability of quasi-geostrophic ellipsoidal vortices. J. Fluid Mech. 536, 401–421.Google Scholar
Dritschel, D. G. & Viúdez, Á. 2003 A balanced approach to modelling rotating stably stratified geophysical flows. J. Fluid Mech. 488, 123–150.Google Scholar
Dritschel, D. G. & Viúdez, Á. 2007 The persistence of balance in geophysical flows. J. Fluid Mech. 570, 365–383.Google Scholar
Ford, R., McIntyre, M. E. & Norton, W. A. 2000 Balance and the slow quasimanifold: some explicit results. J. Atmos. Sci. 57, 1236–1254.Google Scholar
Hashimoto, H., Shimonishi, T. & Miyazaki, T. 1999 Quasigeostrophic ellipsoidal vortices in a two-dimensional strain field. J. Phys. Soc Japan 68 (12), 3863–3880.Google Scholar
Hobson, E. W. 1931 Theory of Spherical and Ellipsoidal Harmonics. Cambridge University Press.Google Scholar
Kida, S. 1981 Motion of an elliptical vortex in a uniform shear flow. J. Phys. Soc. Japan 50, 3517–3520.CrossRefGoogle Scholar
Kirchhoff, G. 1876 Vorlesungen über mathematische Physik: Mechanik. Teubner.Google Scholar
Koshel, K. V., Ryzhov, E. A. & Zhmur, V. V. 2013 Diffusion-affected passive scalar transport in an ellipsoidal vortex in a shear flow. Nonlinear Process. Geophys. 20, 437–444.Google Scholar
Koshel, K. V., Ryzhov, E. A. & Zhmur, V. V. 2015 Effect of the vertical component of diffusion on passive scalar transport in an isolated vortex model. Phys. Rev. E 92, 053021.Google Scholar
Lane, T. P., Doyle, J. D., Plougonven, R., Shapiro, M. A. & Sharman, R. D. 2004 Observations and numerical simulations of inertia–gravity waves and shearing instabilities in the vicinity of a jet stream. J. Atmos. Sci. 61, 2692–2706.Google Scholar
Laplace, P. S. 1784 Théorie du Mouvement et de la Figure Elliptique des Planètes. Imprimerie de Ph.-D. Pierres.Google Scholar
Leith, C. E. 1980 Nonlinear normal mode initialization and quasi-geostrophic theory. J. Atmos. Sci. 37, 958–968.Google Scholar
Love, A. E. H. 1893 On the stability of certain vortex motions. Proc. Lond. Math. Soc. 25, 18–42.Google Scholar
Lyttleton, R. A. 1953 The Stability of Rotating Liquid Masses. Cambridge University Press.Google Scholar
McKiver, W. J. 2015 The ellipsoidal vortex: a novel approach to geophysical turbulence. Adv. Math. Phys. 2015, 613683.Google Scholar
McKiver, W. J. & Dritschel, D. G. 2003 The motion of a fluid ellipsoid in a general linear background flow. J. Fluid Mech. 474, 147–173.Google Scholar
McKiver, W. J. & Dritschel, D. G. 2006 The stability of a quasi-geostrophic ellipsoidal vortex in a background shear flow. J. Fluid Mech. 560, 1–17.Google Scholar
McKiver, W. J. & Dritschel, D. G. 2008 Balance in non-hydrostatic rotating stratified turbulence. J. Fluid Mech. 596, 201–219.Google Scholar
Meacham, S. P. 1992 Quasigeostrophic, ellipsoidal vortices in a stratified fluid. Dyn. Atmos. Oceans 16, 189–223.Google Scholar
Meacham, S. P., Pankratov, K. K., Shchepetkin, A. F. & Zhmur, V. V. 1994 The interaction of ellipsoidal vortices with background shear flows in a stratified fluid. Dyn. Atmos. Oceans 21, 167–212.Google Scholar
Miyazaki, T., Furuichi, Y. & Takahashi, N. 2001 Quasigeostrophic ellipsoidal vortex model. J. Phys. Soc. Japan 70 (7), 1942–1953.Google Scholar
Miyazaki, T., Ueno, K. & Shimonishi, T. 1999 Quasigeostrophic tilted spheroidal vortices. J. Phys. Soc. Japan 68 (8), 2592–2601.Google Scholar
Mohebalhojeh, A. R. 2002 On shallow-water potential-vorticity inversion by Rossby-number expansions. Q. J. R. Meteorol. Soc. 128, 679–694.Google Scholar
Mohebalhojeh, A. R. & Dritschel, D. G. 2001 Hierarchies of balance conditions for the f-plane shallow water equations. J. Atmos. Sci. 58 (16), 2411–2426.Google Scholar
Muraki, D. J., Snyder, C. & Rotunno, R. 1999 The next-order corrections to quasigeostrophic theory. J. Atmos. Sci. 56, 1547–1560.2.0.CO;2>CrossRefGoogle Scholar
Paillet, J., Le Cann, B., Carton, X., Morel, Y. & Serpette, A. 2002 Dynamics and evolution of a northern meddy. J. Phys. Oceanogr. 32, 55–79.Google Scholar
Reinaud, J., Dritschel, D. G. & Koudella, C. R. 2003 The shape of vortices in quasi-geostrophic turbulence. J. Fluid Mech. 474, 175–191.Google Scholar
Schecter, D. A. & Montgomery, M. T. 2003 On the symmetrization rate of an intense geophysical vortex. Dyn. Atmos. Oceans 37, 55–88.CrossRefGoogle Scholar
Schultz-Tokos, K. & Rossby, T. 1991 Kinematics and dynamics of a Mediterranean salt lens. J. Phys. Oceanogr. 21, 879–892.Google Scholar
Shapiro, G. I. & Meschanov, S. L. 1991 Distribution and spreading of Red Sea water and salt lens formation in the northwest Indian Ocean. Deep-Sea Res. 38 (1), 21–34.Google Scholar
Tsang, Y.-K. & Dritschel, D. G. 2015 Ellipsoidal vortices in rotating stratified fluids: beyond the quasi-geostrophic approximation. J. Fluid Mech. 762, 196–231.Google Scholar
Ursella, L., Kovac̆ević, V. & Gac̆ić, M. 2011 Footprints of mesoscale eddy passages in the Strait of Otranto (Adriatic Sea). J. Geophys. Res. 116, C04005.Google Scholar
Vallis, G. K. 1996 Potential vorticity inversion and balanced equations of motion for rotating and stratified flows. Q. J. R. Meteorol. Soc. 122, 291–322.Google Scholar
Vanneste, J. & Yavneh, I. 2004 Exponentially small inertia–gravity waves and the breakdown of quasi-geostrophic balance. J. Atmos. Sci. 61, 211–223.Google Scholar
Viúdez, Á. & Dritschel, D. G. 2004 Optimal potential vorticity balance of geophysical flows. J. Fluid Mech. 521, 343–352.Google Scholar
Viúdez, Á. & Dritschel, D. G. 2006 Spontaneous generation of inertia–gravity wave packets by balanced geophysical flows. J. Fluid Mech. 553, 107–117.Google Scholar
Waite, M. L. & Bartello, P. 2006 The transition from geostrophic to stratified turbulence. J. Fluid Mech. 568, 89–108.Google Scholar
Warn, T., Bokhove, O., Shepherd, T. G. & Vallis, G. K. 1995 Rossby number expansions, slaving principles, and balance dynamics. Q. J. R. Meteorol. Soc. 121, 723–739.Google Scholar