Hostname: page-component-66644f4456-tnr8b Total loading time: 0 Render date: 2025-02-12T16:05:34.351Z Has data issue: true hasContentIssue false
  • English
  • Français

Axisymmetric jet manipulated using two unsteady minijets

Published online by Cambridge University Press:  02 November 2016

H. Yang  and
Y. Zhou
H. Yang
Affiliation:
Institute for Turbulence-Noise-Vibration Interactions and Control, Shenzhen Graduate School, Harbin Institute of Technology, Shenzhen, China Department of Mechanical Engineering, The Hong Kong Polytechnic University, Hong Kong, China
Y. Zhou*
Affiliation:
Institute for Turbulence-Noise-Vibration Interactions and Control, Shenzhen Graduate School, Harbin Institute of Technology, Shenzhen, China Digital Engineering Laboratory of Offshore Equipment, Shenzhen, China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The manipulation of a turbulent axisymmetric jet is experimentally investigated based on two unsteady radial minijets. The Reynolds number is 8000. The mass flow rate ratio 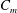$C_{m}$ of the two minijets to that of the main jet and the ratio 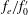$f_{e}/f_{0}^{\prime }$ of the excitation frequency 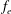$f_{e}$ to the preferred-mode frequency 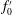$f_{0}^{\prime }$ in the natural jet are examined. The decay rate 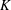$K$ of the jet centreline mean velocity exhibits a strong dependence on 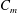$C_{m}$ and 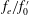$f_{e}/f_{0}^{\prime }$ and is classified into three distinct categories in terms of required 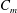$C_{m}$, achievable enhancement in 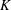$K$ and flow physics involved. Great effort is made to understand the flow physics associated with the first category of the manipulated jet, under which 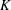$K$ can be immensely improved with a very small 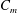$C_{m}$. Detailed measurements are conducted upstream and downstream of the nozzle exit using hot-wire, flow visualization and particle imaging velocimetry techniques. Whilst strong entrainment is predominant in the injection plane of the minijets, rapid spread occurs in the orthogonal non-injection plane. Three types of coherent structures are identified, i.e. the contorted ring vortex, two pairs of streamwise vortices and mushroom-like counter-rotating structures sequentially ‘tossed’ out radially in the non-injection plane. Their interactions account for the large rise in 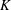$K$. The unsteady disturbance of the minijets is found to play a key role in the formation and interaction of these vortices, which are distinct from those formed under the manipulation of steady minijets and other techniques. A conceptual model of the flow structure under manipulation is proposed.

JFM classification

Flow Control: Flow Control Wakes/Jets: Jets Flow Control: Mixing enhancement
Type
Papers
Information
Journal of Fluid Mechanics , Volume 808 , 10 December 2016 , pp. 362 - 396
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alkislar, M. B., Krothapalli, A. & Butler, G. W. 2007 The effect of streamwise vortices on the aeroacoustics of a mach 0.9 jet. J. Fluid Mech. 578, 139–169.Google Scholar
Alvi, F. S., Lou, H., Shih, C. & Kumar, R. 2008 Experimental study of physical mechanisms in the control of supersonic impinging jets using microjets. J. Fluid Mech. 613, 55–83.Google Scholar
Annaswamy, A. M., Choi, J. J. & Alvi, F. S. 2008 Pulsed microjet control of supersonic impinging jets via low-frequency excitation. Proc. Inst. Mech. Engrs I 222 (5), 279–296.Google Scholar
Arakeri, V. H., Krothapalli, A., Siddavaram, V., Alkislar, M. B. & Lourenco, L. M. 2003 On the use of microjets to suppress turbulence in a mach 0.9 axisymmetric jet. J. Fluid Mech. 490, 75–98.Google Scholar
Bernal, L. P. & Roshko, A. 1986 Streamwise vortex structure in plane mixing layers. J. Fluid Mech. 170, 499–525.CrossRefGoogle Scholar
Bradbury, L. J. S. & Khadem, A. H. 1975 The distortion of a jet by tabs. J. Fluid Mech. 70, 801–813.Google Scholar
Brancher, P., Chomaz, J. M. & Huerre, P. 1994 Direct numerical simulations of round jets: Vortex induction and side jets. Phys. Fluids 6 (5), 1768–1774.CrossRefGoogle Scholar
Breidenthal, R. E. 2008 The effect of acceleration on turbulent entrainment. Phys. Scr. T 132, 014001.Google Scholar
Browand, F. K. & Ho, C.-M. 1983 The mixing layer: an example of quasi two-dimensional turbulence. J. Theor. Appl. Mech. 1, 99–120.Google Scholar
Cattafesta, L. N. III & Sheplak, M. 2011 Actuators for active flow control. Annu. Rev. Fluid Mech. 43, 247–272.Google Scholar
Choi, J. J., Annaswamy, A. M., Lou, H. & Alvi, F. S. 2006 Active control of supersonic impingement tones using steady and pulsed microjets. Exp. Fluids 41 (6), 841–855.Google Scholar
Cohen, J. & Wygnanski, I. 1987a The evolution of instabilities in the axisymmetric jet. Part 1. The linear growth of disturbances near the nozzle. J. Fluid Mech. 176, 191–219.Google Scholar
Cohen, J. & Wygnanski, I. 1987b The evolution of instabilities in the axisymmetric jet. Part 2. The flow resulting from the interaction between two waves. J. Fluid Mech. 176, 221–235.Google Scholar
Corke, T. C., Enloe, C. L. & Wilkinson, S. P. 2010 Dielectric barrier discharge plasma actuators for flow control. Annu. Rev. Fluid Mech. 42, 505–529.CrossRefGoogle Scholar
Cortelezzi, L. & Karagozian, A. R. 2001 On the formation of the counter-rotating vortex pair in transverse jets. J. Fluid Mech. 446, 347–373.CrossRefGoogle Scholar
Crighton, D. G. & Gaster, M. 1976 Stability of slowly diverging jet flow. J. Fluid Mech. 77, 397–413.Google Scholar
Davis, M. R. 1982 Variable control of jet decay. AIAA J. 20 (5), 606–609.Google Scholar
Fiedler, H. E. & Mensing, P. 1985 The plane turbulent shear layer with periodic excitation. J. Fluid Mech. 150, 281–309.CrossRefGoogle Scholar
Freund, B. J. & Moin, P. 2000 Jet mixing enhancement by high-amplitude fluidic actuation. AIAA J. 38 (10), 1863–1870.Google Scholar
Freymuth, P. 1966 On transition in a separated laminar boundary layer. J. Fluid Mech. 25, 683–704.Google Scholar
Ginevsky, A. S., Vlasov, Y. V. & Karavosov, R. K. 2004 Acoustic Control of Turbulent Jets. Springer.Google Scholar
Glezer, A. & Amitay, M. 2002 Synthetic jets. Annu. Rev. Fluid Mech. 34, 503–529.Google Scholar
Gutmark, E. & Ho, C.-M. 1983 Preferred modes and the spreading rates of jets. Phys. Fluids 26 (10), 2932–2938.Google Scholar
Gutmark, E. J. & Grinstein, F. F. 1999 Flow control with noncircular jets. Annu. Rev. Fluid Mech. 31, 239–272.Google Scholar
Henderson, B. 2010 Fifty years of fluidic injection for jet noise reduction. Intl J. Aeroacoust. 9 (1), 91–122.Google Scholar
Ho, C. & Gutmark, E. 1987 Vortex induction and mass entrainment in a small-aspect-ratio elliptic jet. J. Fluid Mech. 179, 383–405.Google Scholar
Ho, C.-M. & Huang, L.-S. 1982 Subharmonics and vortex merging in mixing layers. J. Fluid Mech. 119, 443–473.Google Scholar
Ho, C.-M. & Huerre, P. 1984 Perturbed free shear layers. Annu. Rev. Fluid Mech. 16, 365–424.Google Scholar
Huang, J. F., Zhou, Y. & Zhou, T. 2006 Three-dimensional structure measurement using a modified PIV technique. Exp. Fluids 40 (6), 884–896.Google Scholar
Husain, H. S. & Hussain, F. 1991 Elliptic jets. Part 2. Dynamics of coherent structures: pairing. J. Fluid Mech. 233, 439–482.Google Scholar
Husain, H. S. & Hussain, F. 1993 Elliptic jets. Part 3. Dynamics of preferred mode coherent structure. J. Fluid Mech. 248, 315–361.Google Scholar
Hussain, A. K. M. F. 1986 Coherent structures and turbulence. J. Fluid Mech. 173, 303–356.CrossRefGoogle Scholar
Hussain, A. K. M. F. & Zaman, K. B. M. Q. 1980 Vortex pairing in a circular jet under controlled excitation. Part 2. Coherent structure dynamics. J. Fluid Mech. 101 (3), 493–544.Google Scholar
Hussain, A. K. M. F. & Zedan, M. F. 1978 Effects of the initial condition on the axisymmetric free shear layer: effect of the initial fluctuation level. Phys. Fluids 21, 1475–1481.Google Scholar
Hussain, F. & Husain, H. S. 1989 Elliptic jets. Part 1. Characteristics of unexcited and excited jets. J. Fluid Mech. 208, 257–320.Google Scholar
Hussein, J. H., Capp, S. P. & George, W. K. 1994 Velocity measurements in a high-Reynolds-number, momentum-conserving, axisymmetric, turbulent jet. J. Fluid Mech. 258, 31–75.CrossRefGoogle Scholar
Ibrahim, M. K., Kunimura, R. & Nakamura, Y. 2002 Mixing enhancement of compressible jets by using unsteady microjets as actuators. AIAA J. 40 (4), 681–688.Google Scholar
Johari, H., Pacheco-Tougas, M. & Hermanson, J. C. 1999 Penetration and mixing of fully modulated turbulent jets in crossflow. AIAA J. 37 (7), 842–850.Google Scholar
Lardeau, S., Lamballais, E. & Bonnet, J. P. 2002 Direct numerical simulation of a jet controlled by fluid injection. J. Turbul. 3, N2.Google Scholar
Lasheras, J. C., Cho, J. S. & Maxworthy, T. 1986 On the origin and evolution of streamwise vortical structures in a plane, free shear layer. J. Fluid Mech. 172, 231–258.CrossRefGoogle Scholar
Lasheras, J. C. & Choi, H. 1988 Three-dimensional instability of a plane free shear layer: an experimental study of the formation and evolution of streamwise vortices. J. Fluid Mech. 189, 53–86.Google Scholar
Liepmann, D. & Gharib, M. 1992 The role of streamwise vorticity in the near-field entrainment of round jets. J. Fluid Mech. 245, 643–668.Google Scholar
Longmire, E. K. & Duong, L. H. 1996 Bifurcating jets generated with stepped and sawtooth nozzles. Phys. Fluids 8 (4), 978–992.Google Scholar
Martin, J. E. & Meiburg, E. 1991 Numerical investigation of three-dimensionally evolving jets subject to axisymmetric and azimuthal perturbations. J. Fluid Mech. 230, 271–318.Google Scholar
M’Closkey, R. T., King, J. M., Cortelezzi, L. & Karagozian, A. R. 2002 The actively controlled jet in crossflow. J. Fluid Mech. 452, 325–335.Google Scholar
Melling, A. 1997 Tracer particles and seeding for particle image velocimetry. Meas. Sci. Technol. 8, 1406–1416.Google Scholar
Mi, J., Kalt, P., Nathan, G. J. & Wong, C. Y. 2007 PIV measurements of a turbulent jet issuing from round sharp-edged plate. Exp. Fluids 42 (4), 625–637.Google Scholar
Mi, J., Nathan, G. J. & Luxton, R. E. 2000 Centreline mixing characteristics of jets from nine differently shaped nozzles. Exp. Fluids 28, 93–94.Google Scholar
Michalke, A. 1965a Vortex formation in a free boundary layer according to stability theory. J. Fluid Mech. 22, 371–383.Google Scholar
Michalke, A. 1965b On spatially growing disturbances in an inviscid shear layer. J. Fluid Mech. 23, 521–544.Google Scholar
Monkewitz, P. A. & Bechert, D. W. 1988 Self-excited oscillations and mixing in a hot jet. Phys. Fluids 31 (9), 2386.Google Scholar
Monkewitz, P. A., Bechert, D. W., Barsikow, B. & Lehmann, B. 1990 Self-excited oscillations and mixing in a heated round jet. J. Fluid Mech. 213, 611–639.Google Scholar
Monkewitz, P. A., Lehmann, B., Barsikow, B. & Bechert, D. W. 1989 The spreading of self-excited hot jets by side jets. Phys. Fluids A 1, 446–448.Google Scholar
Monkewitz, P. A. & Pfizenmaier, E. 1991 Mixing by side jets in strongly forced and selfexcited round jets. Phys. Fluids A 3, 1356–1361.Google Scholar
Moreau, E. 2007 Airflow control by non-thermal plasma actuators. J. Phys. D: Appl. Phys. 40 (3), 605–636.Google Scholar
New, T. H. & Tay, W. L. 2006 Effects of cross-stream radial injections on a round jet. J. Turbul. 7, N57.Google Scholar
New, T. H. & Tsovolos, D. 2012 Vortex behaviour and velocity characteristics of jets issuing from hybrid inclined elliptic nozzles. Flow Turbul. Combust. 89 (4), 601–625.Google Scholar
Oberleithner, K., Paschereit, C. O. & Wygnanski, I. 2014 On the impact of swirl on the growth of coherent structures. J. Fluid Mech. 741, 156–199.Google Scholar
Parekh, D. E., Kibens, V., Glezer, A., Wiltse, J. M. & Smith, D. M. 1996 Innovative jet flow control: mixing enhancement experiments. AIAA Paper 96–0308.Google Scholar
Pattenden, R. J., Turnock, S. R. & Zhang, X. 2005 Measurements of the flow over a low-aspect-ratio cylinder mounted on a ground plane. Exp. Fluids 39 (1), 10–21.Google Scholar
Raman, G. 1997 Using controlled unsteady fluid mass addition to enhance jet mixing. AIAA J. 35 (4), 647–656.Google Scholar
Raman, G. & Cornelius, D. 1995 Jet mixing control using excitation from miniature oscillating jets. AIAA J. 33 (2), 365–368.Google Scholar
Reeder, M. F. & Samimy, M. 1996 The evolution of a jet with vortex-generating tabs: real-time visualization and quantitative measurements. J. Fluid Mech. 311, 73–118.Google Scholar
Reynolds, W. C., Parekh, D. E., Juvet, P. J. D. & Lee, M. J. D. 2003 Bifurcating and blooming jets. Annu. Rev. Fluid Mech. 35, 295–315.Google Scholar
Samimy, M., Kim, J. H., Kastner, J., Adamovich, I. & Utkin, Y. 2007 Active control of high-speed and high-Reynolds-number jets using plasma actuators. J. Fluid Mech. 578, 305–330.Google Scholar
Seidel, J. F., Pappart, C., New, T. H. & Tsai, H. M.2005 Effects of multiple radial blowing around a circular jet. AIAA Paper 2005-866.Google Scholar
Smith, B. L. & Glezer, A. 1998 The formation and evolution of synthetic jets. Phys. Fluids 10 (9), 2281–2297.CrossRefGoogle Scholar
Smith, B. L. & Glezer, A. 2002 Jet vectoring using synthetic jets. J. Fluid Mech. 458, 1–34.Google Scholar
Suzuki, H., Kasagi, N. & Suzuki, Y. 2004 Active control of an axisymmetric jet with distributed electromagnetic flap actuators. Exp. Fluids 36 (3), 498–509.Google Scholar
Tamburello, D. A. & Amitay, M. 2006 Manipulation of an axisymmetric jet using continuous control jets. J. Turbul. 7, N59.Google Scholar
Tamburello, D. A. & Amitay, M. 2007 Three-dimensional interactions of a free jet with a perpendicular synthetic jet. J. Turbul. 8, N38.Google Scholar
Webster, D. R. & Longmire, E. K. 1997 Vortex dynamics in jets from inclined nozzles. Phys. Fluids 9 (3), 655–666.Google Scholar
Wiltse, J. M. & Glezer, A. 1993 Manipulation of free shear flows using piezoelectric actuators. J. Fluid Mech. 249, 261–285.Google Scholar
Yang, H., Zhou, Y., So, R. M. C. & Liu, Y. 2016 Turbulent jet manipulation using two unsteady azimuthally separated radial minijets. Proc. R. Soc. A 472, 0417.Google Scholar
Yule, A. J. 1978 Large-scale structure in the mixing layer of a round jet. J. Fluid Mech. 89, 413–432.Google Scholar
Zaman, K. B. M. Q. 1996 Axis switching and spreading of an asymmetric jet: the role of coherent structure dynamics. J. Fluid Mech. 316, 1–27.Google Scholar
Zaman, K. B. M. Q. 1999 Spreading characteristics of compressible jets from nozzles of various geometries. J. Fluid Mech. 383, 197–228.Google Scholar
Zaman, K. B. M. Q. & Hussain, A. K. M. F. 1980 Vortex pairing in a circular jet under controlled excitation. Part 1. General jet response. J. Fluid Mech. 101, 449–491.Google Scholar
Zaman, K. B. M. Q., Reeder, M. F. & Samimy, M. 1994 Control of an axisymmetric jet using vortex generators. Phys. Fluids 6 (2), 778–793.Google Scholar
Zhang, P.2014 Active control of a turbulent round jet based on unsteady microjets. PhD thesis, The Hong Kong Polytechnic University.Google Scholar
Zhang, Q. & Johari, H. 1996 Effects of acceleration on turbulent jets. Phys. Fluids 8 (8), 2185–2195.Google Scholar
Zhou, Y., Du, C., Mi, J. & Wang, X. W. 2012 Turbulent round jet control using two steady mini-jets. AIAA J. 50 (3), 736–740.Google Scholar