Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-24T21:19:37.308Z Has data issue: false hasContentIssue false
  • English
  • Français

Axisymmetric flows on the torus geometry

Published online by Cambridge University Press:  24 August 2020

Sergiu Busuioc Open the ORCID record for Sergiu Busuioc [Opens in a new window] ,
H. Kusumaatmaja Open the ORCID record for H. Kusumaatmaja [Opens in a new window]  and
Victor E. Ambruş Open the ORCID record for Victor E. Ambruş [Opens in a new window]
Sergiu Busuioc
Affiliation:
School of Engineering, University of Edinburgh, EdinburghEH9 3FB, UK
H. Kusumaatmaja*
Affiliation:
Department of Physics, Durham University, DurhamDH1 3LE, UK
Victor E. Ambruş*
Affiliation:
Department of Physics, West University of Timişoara, Timişoara300223, Romania Department of Mathematics and Statistics, Old Dominion University, Norfolk, VA23529, USA
*
†Email addresses for correspondence: [email protected], [email protected]
†Email addresses for correspondence: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

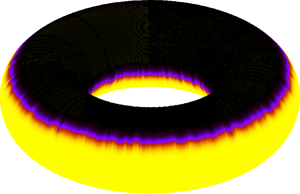
We present a series of analytically solvable axisymmetric flows on the torus geometry. For the single-component flows, we describe the propagation of sound waves for perfect fluids, as well as the viscous damping of shear and longitudinal waves for isothermal and thermal fluids. Unlike the case of planar geometry, the non-uniform curvature on a torus necessitates a distinct spectrum of eigenfrequencies and their corresponding basis functions. This has several interesting consequences, including breaking the degeneracy between even and odd modes, a lack of periodicity even in the flows of perfect fluids and the loss of Galilean invariance for flows with velocity components in the poloidal direction. For the multi-component flows, we study the equilibrium configurations and relaxation dynamics of axisymmetric fluid stripes, described using the Cahn–Hilliard equation. We find a second-order phase transition in the equilibrium location of the stripe as a function of its area ${\rm \Delta} A$. This phase transition leads to a complex dependence of the Laplace pressure on ${\rm \Delta} A$. We also derive the underdamped oscillatory dynamics as the stripes approach equilibrium. Furthermore, relaxing the assumption of axial symmetry, we derive the conditions under which the stripes become unstable. In all cases, the analytical results are confirmed numerically using a finite-difference Navier–Stokes solver.

JFM classification

Mathematical Foundations: General fluid mechanics Multiphase and Particle-laden Flows: Multiphase flow
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 901 , 25 October 2020 , A9
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Al-Izzi, S. C., Sens, P. & Turner, M. S. 2018 Shear-driven instabilities of membrane tubes and dynamin-induced scission. arXiv:1810.05862.Google Scholar
Ambruş, V. E., Busuioc, S., Wagner, A. J., Paillusson, F. & Kusumaatmaja, H. 2019 Multicomponent flow on curved surfaces: a vielbein lattice Boltzmann approach. Phys. Rev. E 100, 063306.CrossRefGoogle ScholarPubMed
Arroyo, M. & Desimone, A. 2009 Relaxation dynamics of fluid membranes. Phys. Rev. E 79, 039906.CrossRefGoogle ScholarPubMed
Bertalmío, M., Cheng, L.-T., Osher, S. & Sapiro, G. 2001 Variational problems and partial differential equations on implicit surfaces. J. Comput. Phys. 174 (2), 759–780.CrossRefGoogle Scholar
Boozer, A. H. 2005 Physics of magnetically confined plasmas. Rev. Mod. Phys. 76, 1071–1141.CrossRefGoogle Scholar
Briant, A. J. & Yeomans, J. M. 2004 Lattice Boltzmann simulations of contact line motion. Part 2. Binary fluids. Phys. Rev. E 69, 031603.CrossRefGoogle Scholar
Busuioc, S. & Ambruş, V. E. 2019 Lattice Boltzmann models based on the vielbein formalism for the simulation of flows in curvilinear geometries. Phys. Rev. E 99, 033304.CrossRefGoogle ScholarPubMed
Busuioc, S., Ambruş, V. E., Biciuşcă, T. & Sofonea, V. 2020 Two-dimensional off-lattice Boltzmann model for van der Waals fluids with variable temperature. Comput. Maths Applics. 79, 111–140.CrossRefGoogle Scholar
Cox, S., Weaire, D. & Glazier, J. A. 2004 The rheology of two-dimensional foams. Rheol. Acta 43, 442–448.CrossRefGoogle Scholar
Dziuk, G. & Elliott, C. M. 2007 Surface finite elements for parabolic equations. J. Comput. Math. 25, 385–407.Google Scholar
Dziuk, G. & Elliott, C. M. 2013 Finite element methods for surface PDEs. Acta Numerica 22, 289–396.CrossRefGoogle Scholar
Fonda, P., Rinaldin, M., Kraft, D. J. & Giomi, L. 2018 Interface geometry of binary mixtures on curved substrates. Phys. Rev. E 98, 032801.CrossRefGoogle Scholar
Giordanelli, I., Mendoza, M. & Herrmann, H. J. 2018 Modelling electron-phonon interactions in graphene with curved space hydrodynamics. Sci. Rep. 8, 12545.CrossRefGoogle ScholarPubMed
Gross, B. J. & Atzberger, P. J. 2018 Hydrodynamic flows on curved surfaces: spectral numerical methods for radial manifold shapes. J. Comput. Phys. 371, 663–689.CrossRefGoogle Scholar
Henkes, S., Marchetti, M. C. & Sknepnek, R. 2018 Dynamical patterns in nematic active matter on a sphere. Phys. Rev. E 97, 042605.CrossRefGoogle Scholar
Henle, M. L. & Levine, A. J. 2010 Hydrodynamics in curved membranes: the effect of geometry on particulate mobility. Phys. Rev. E 81, 011905.CrossRefGoogle ScholarPubMed
Janssen, L. M. C., Kaiser, A. & Löwen, H. 2017 Aging and rejuvenation of active matter under topological constraints. Sci. Rep. 7, 5667.CrossRefGoogle ScholarPubMed
Keber, F. C., Loiseau, E., Sanchez, T., DeCamp, S. J., Giomi, L., Bowick, M. J., Marchetti, M. C., Dogic, Z. & Bausch, A. R. 2014 Topology and dynamics of active nematic vesicles. Science 345, 1135–1139.CrossRefGoogle ScholarPubMed
Koba, H. 2018 On derivation of compressible fluid systems on an evolving surface. Q. Appl. Maths 76, 303–359.CrossRefGoogle Scholar
Koba, H., Liu, C. & Giga, Y. 2017 Energetic variational approaches for incompressible fluid systems on an evolving surface. Q. Appl. Maths 75, 359–389.CrossRefGoogle Scholar
Krüger, T., Kusumaatmaja, H., Kuzmin, A., Shardt, O., Silva, G. & Viggen, E. M. 2017 Lattice Boltzmann Method: Principles and Practice. Springer.CrossRefGoogle Scholar
Macdonald, C. & Ruuth, S. 2010 The implicit closest point method for the numerical solution of partial differential equations on surfaces. SIAM J. Sci. Comput. 31 (6), 4330–4350.CrossRefGoogle Scholar
Marsden, J. E. & Hughes, J. R. 1994 Mathematical Foundations of Elasticity. Dover.Google Scholar
Nitschke, I., Reuther, S. & Voigt, A. 2017 Discrete exterior calculus (DEC) for the surface Navier–Stokes equation. In Transport Processes at Fluidic Interfaces (ed. Bothe, D. & Reusken, A.), pp. 125–263. Birkhäuser.Google Scholar
Nitschke, I., Reuther, S. & Voigt, A. 2019 Hydrodynamic interactions in polar liquid crystals on evolving surfaces. Phys. Rev. Fluids 4, 044002.CrossRefGoogle Scholar
Nitschke, I., Voigt, A. & Wensch, J. 2012 A finite element approach to incompressible two-phase flow on manifolds. J. Fluid Mech. 708, 418–438.CrossRefGoogle Scholar
Olver, F. W. J., Lozier, D. W., Boisvert, R. F. & Clark, C. W. 2010 NIST Handbook of Mathematical Functions. Cambridge University Press.Google Scholar
Pearce, D. J. G., Ellis, P. W., Fernandez-Nieves, A. & Giomi, L. 2019 Geometrical control of active turbulence in curved topographies. Phys. Rev. Lett. 122, 168002.CrossRefGoogle ScholarPubMed
Rätz, A. & Voigt, A. 2006 PDE's on surfaces – a diffuse interface approach. Commun. Math. Sci. 4, 575–590.CrossRefGoogle Scholar
Rembiasz, T., Obergaulinger, M., Cerdá-Durán, P., Aloy, M.-Á. & Müller, E. 2017 On the measurements of numerical viscosity and resistivity in Eulerian MHD codes. Astrophys. J. Suppl. 230, 18.CrossRefGoogle Scholar
Reuther, S. & Voigt, A. 2018 Solving the incompressible surface Navier–Stokes equation by surface finite elements. Phys. Fluids 30 (1), 012107.CrossRefGoogle Scholar
Rieutord, M. 2015 Fluid Dynamics: An Introduction. Springer.Google Scholar
Sasaki, E., Takehiro, S. & Yamada, M. 2015 Bifurcation structure of two-dimensional viscous zonal flows on a rotating sphere. J. Fluid Mech. 774, 224–244.CrossRefGoogle Scholar
Serrin, J. 1959 Mathematical principles of classical fluid mechanics. In Encyclopedia of Physics (ed. Flügge, S. & Truesdell, C.), Fluid dynamics I, vol. VIII/1, pp. 125–263. Springer.Google Scholar
Shan, X. 2006 Analysis and reduction of the spurious current in a class of multiphase lattice Boltzmann models. Phys. Rev. E 73, 047701.CrossRefGoogle Scholar
Sofonea, V., Biciuşcă, T., Busuioc, S., Ambruş, V. E., Gonnella, G. & Lamura, A. 2018 Corner-transport-upwind lattice Boltzmann model for bubble cavitation. Phys. Rev. E 97, 023309.CrossRefGoogle ScholarPubMed
Sofonea, V., Lamura, A., Gonnella, G. & Cristea, A. 2004 Finite-difference lattice Boltzmann model with flux limiters for liquid-vapor systems. Phys. Rev. E 70, 046702.CrossRefGoogle ScholarPubMed
Sofonea, V. & Sekerka, R. F. 2003 Viscosity of finite difference lattice Boltzmann models. J. Comput. Phys. 184, 422–434.CrossRefGoogle Scholar
Taylor, M. E. 2011 Partial Differential Equations III: Nonlinear Equations, 2nd edn. Springer.CrossRefGoogle Scholar
Torres-Sánchez, A., Millán, D. & Arroyo, M. 2019 Modelling fluid deformable surfaces with an emphasis on biological interfaces. J. Fluid Mech. 872, 218–271.CrossRefGoogle Scholar
Voigt, A. 2019 Fluid deformable surfaces. J. Fluid Mech. 878, 1–4.CrossRefGoogle Scholar

Busuioc et al. supplementary movie 1

Development of the instability under azimuthal perturbations of a fluid stripe centred on eq c = 0:86 on the torus with a = 0:4. [See Fig. 15(a) for further details]

Download Busuioc et al. supplementary movie 1(Video)
Video 3 MB

Busuioc et al. supplementary movie 2

Development of the instability under azimuthal perturbations of a fluid stripe centred on hetaeq c = 0:65 on the torus with a = 0:4. [See Fig. 15(b) for further details]

Download Busuioc et al. supplementary movie 2(Video)
Video 1.5 MB
Supplementary material: PDF

Busuioc et al. supplementary material

Supplementary data

Download Busuioc et al. supplementary material(PDF)
PDF 1.4 MB