Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-24T14:36:32.678Z Has data issue: false hasContentIssue false
  • English
  • Français

Axisymmetric displacement flows in fluid-driven fractures

Published online by Cambridge University Press:  15 December 2022

Sri Savya Tanikella  and
Emilie Dressaire Open the ORCID record for Emilie Dressaire [Opens in a new window]
Sri Savya Tanikella
Affiliation:
Department of Mechanical Engineering, University of California Santa Barbara, Santa Barbara, CA 93106, USA
Emilie Dressaire*
Affiliation:
Department of Mechanical Engineering, University of California Santa Barbara, Santa Barbara, CA 93106, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

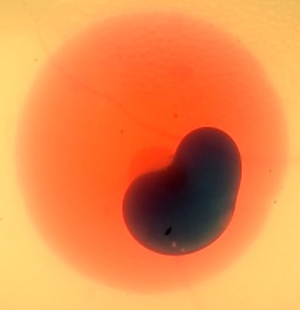
Displacement flows are common in hydraulic fracturing, as fracking fluids of different composition are injected sequentially in the fracture. The injection of an immiscible fluid at the centre of a liquid-filled fracture results in the growth of the fracture and the outward displacement of the interface between the two liquids. We study the dynamics of the fluid-driven fracture, which is controlled by the competition between viscous, elastic and toughness-related stresses. We use a model experiment to characterize the dynamics of the fracture for a range of mechanical properties of the fractured material and fracturing fluids. We form the liquid-filled pre-fracture in an elastic brittle matrix of gelatin. The displacing liquid is then injected. We record the radius and aperture of the fracture, and the position of the interface between the two liquids. In a typical experiment, the axisymmetric radial viscous flow is accommodated by the elastic deformation and fracturing of the matrix. We model the coupling between elastic deformation, viscous dissipation and fracture propagation, and recover the two fracturing regimes identified for single-fluid injection. For the viscous-dominated and toughness-dominated regimes, we derive scaling equations that describe the crack growth due to a displacement flow and show the influence of the pre-existing fracture on the crack dynamics through a finite initial volume and an average viscosity of the fluids in the fracture.

JFM classification

Aerodynamics: Flow-structure interactions Multiphase and Particle-laden Flows: Multiphase flow
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 953 , 25 December 2022 , A36
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Al-Housseiny, T.T. & Stone, H.A. 2013 Controlling viscous fingering in tapered Hele-Shaw cells. Phys. Fluids 25 (9), 092102–12.CrossRefGoogle Scholar
Al-Housseiny, T.T., Tsai, P.A. & Stone, H.A. 2012 Control of interfacial instabilities using flow geometry. Nat. Phys. 8 (10), 747–750.CrossRefGoogle Scholar
Alessi, D.S., Zolfaghari, A., Kletke, S., Gehman, J., Allen, D.M. & Goss, G.G. 2017 Comparative analysis of hydraulic fracturing wastewater practices in unconventional shale development: water sourcing, treatment and disposal practices. Can. Water Resour. J. 42 (2), 1–17.CrossRefGoogle Scholar
Bao, X. & Eaton, D.W. 2016 Fault activation by hydraulic fracturing in western Canada. Science 354 (6318), 1406–1409.CrossRefGoogle ScholarPubMed
Barbati, A.C., Desroches, J., Robisson, A. & McKinley, G.H. 2016 Complex fluids and hydraulic fracturing. Annu. Rev. Chem. Biomol. Engng 7 (1), 415–453.CrossRefGoogle ScholarPubMed
Barboza, B.R., Chen, B. & Li, C. 2021 A review on proppant transport modelling. J. Petrol. Sci. Engng 204, 108753.CrossRefGoogle Scholar
Barenblatt, G.I. 1956 On the formation of horizontal cracks in hydraulic fracture of an oil-bearing stratum. Prikl. Mat. Mech. 20, 475–486.Google Scholar
Baumberger, T. & Ronsin, O. 2020 Environmental control of crack propagation in polymer hydrogels. Mech. Soft Mater. 2 (1), 14.CrossRefGoogle Scholar
Bessmertnykh, A., Dontsov, E. & Ballarini, R. 2021 Semi-infinite hydraulic fracture driven by a sequence of power-law fluids. J. Eng. Mech. 147 (10), 04021064.Google Scholar
Bunger, A.P. 2006 A photometry method for measuring the opening of fluid-filled fractures. Meas. Sci. Technol. 17 (12), 3237.CrossRefGoogle Scholar
Bunger, A.P. & Detournay, E. 2005 Asymptotic solution for a penny-shaped near-surface hydraulic fracture. Engng Fract. Mech. 72 (16), 2468–2486.CrossRefGoogle Scholar
Bunger, A.P. & Detournay, E. 2008 Experimental validation of the tip asymptotics for a fluid-driven crack. J. Mech. Phys. Solids 56 (11), 3101–3115.CrossRefGoogle Scholar
Bunger, A.P., Gordeliy, E. & Detournay, E. 2013 Comparison between laboratory experiments and coupled simulations of saucer-shaped hydraulic fractures in homogeneous brittle-elastic solids. J. Mech. Phys. Solids 61 (7), 1636–1654.CrossRefGoogle Scholar
Caulk, R.A., Ghazanfari, E., Perdrial, J.N. & Perdrial, N. 2016 Experimental investigation of fracture aperture and permeability change within enhanced geothermal systems. Geothermics 62, 12–21.CrossRefGoogle Scholar
Chen, J.-D. 1989 Growth of radial viscous fingers in a Hele-Shaw cell. J. Fluid Mech. 201, 223–242.CrossRefGoogle Scholar
Chen, Y.-F., Fang, S., Wu, D.-S. & Hu, R. 2017 Visualizing and quantifying the crossover from capillary fingering to viscous fingering in a rough fracture. Water Resour. Res. 53 (9), 7756–7772.CrossRefGoogle Scholar
Cottin, C., Bodiguel, H. & Colin, A. 2010 Drainage in two-dimensional porous media: from capillary fingering to viscous flow. Phys. Rev. E 82 (4), 046315.CrossRefGoogle ScholarPubMed
Cueto-Felgueroso, L. & Juanes, R. 2013 Forecasting long-term gas production from shale. Proc. Natl Acad. Sci. USA 110 (49), 19660–19661.CrossRefGoogle ScholarPubMed
Desroches, J., Detournay, E., Lenoach, B., Papanastasiou, P., Pearson, J.R.A., Thiercelin, M. & Cheng, A. 1994 The crack tip region in hydraulic fracturing. Proc. R. Soc. Lond. A 447 (1929), 39–48.Google Scholar
Detournay, E. 2004 Propagation regimes of fluid-driven fractures in impermeable rocks. Intl J. Geomech. 4 (1), 35–45.CrossRefGoogle Scholar
Detournay, E. 2016 Mechanics of hydraulic fractures. Annu. Rev. Fluid Mech. 48 (1), 311–339.CrossRefGoogle Scholar
Detournay, E. & Garagash, D.I. 2003 The near-tip region of a fluid-driven fracture propagating in a permeable elastic solid. J. Fluid Mech. 494, 1–32.CrossRefGoogle Scholar
Detournay, E. & Peirce, A. 2014 On the moving boundary conditions for a hydraulic fracture. Intl J. Engng Sci. 84, 147–155.CrossRefGoogle Scholar
Garagash, D.I. & Detournay, E. 2000 The tip region of a fluid-driven fracture in an elastic medium. Trans. ASME J. Appl. Mech. 67 (1), 183–192.CrossRefGoogle Scholar
Garagash, D.I. & Detournay, E. 2005 Plane-strain propagation of a fluid-driven fracture: small toughness solution. Trans. ASME J. Appl. Mech. 72 (6), 916–928.CrossRefGoogle Scholar
Giuseppe, E.D., Funiciello, F., Corbi, F., Ranalli, G. & Mojoli, G. 2009 Gelatins as rock analogs: a systematic study of their rheological and physical properties. Tectonophysics 473 (3–4), 391–403.CrossRefGoogle Scholar
Glass, R.J., Rajaram, H. & Detwiler, R.L. 2003 Immiscible displacements in rough-walled fractures: competition between roughening by random aperture variations and smoothing by in-plane curvature. Phys. Rev. E 68 (6), 061110.CrossRefGoogle ScholarPubMed
Homsy, G.M. 1987 Viscous fingering in porous media. Annu. Rev. Fluid Mech. 19 (1), 271–311.CrossRefGoogle Scholar
Hormozi, S. & Frigaard, I.A. 2017 Dispersion of solids in fracturing flows of yield stress fluids. J. Fluid Mech. 830, 93–137.CrossRefGoogle Scholar
Huppert, H.E. & Neufeld, J.A. 2013 The fluid mechanics of carbon dioxide sequestration. Annu. Rev. Fluid Mech. 46 (1), 255–272.CrossRefGoogle Scholar
Jia, B., Tsau, J.-S. & Barati, R. 2019 A review of the current progress of CO2 injection EOR and carbon storage in shale oil reservoirs. Fuel 236, 404–427.CrossRefGoogle Scholar
Kanninen, M.F. & Popelar, C.H. 1985 Advanced Fracture Mechanics. Oxford Engineering Science Series, vol. 15. Oxford University Press.Google Scholar
Kavanagh, J.L., Menand, T. & Daniels, K.A. 2013 Gelatine as a crustal analogue: determining elastic properties for modelling magmatic intrusions. Tectonophysics 582, 101–111.CrossRefGoogle Scholar
Khristianovic, S.A. & Zheltov, Y.P. 1955 Formation of vertical fractures by means of highly viscous liquid. 4th World Petrol. Congr. Proc. OnePetro 2, 576–586.Google Scholar
Lai, C.-Y., Rallabandi, B., Perazzo, A., Zheng, Z., Smiddy, S.E. & Stone, H.A. 2018 Foam-driven fracture. Proc. Natl Acad. Sci. USA 115 (32), 8082–8086.CrossRefGoogle ScholarPubMed
Lai, C.-Y., Zheng, Z., Dressaire, E. & Stone, H.A. 2016 Fluid-driven cracks in an elastic matrix in the toughness-dominated limit. Phil. Trans. R. Soc. Lond. A 374 (2078), 20150425.Google Scholar
Lai, C.-Y., Zheng, Z., Dressaire, E., Wexler, J.S. & Stone, H.A. 2015 Experimental study on penny-shaped fluid-driven cracks in an elastic matrix. Proc. R. Soc. Lond. A 471 (2182), 20150255.Google Scholar
Lecampion, B., Desroches, J., Jeffrey, R.G. & Bunger, A.P. 2017 Experiments versus theory for the initiation and propagation of radial hydraulic fractures in low-permeability materials.. J. Geophys. Res. 122 (2), 1239–1263.CrossRefGoogle Scholar
Lenormand, R., Touboul, E. & Zarcone, C. 1988 Numerical models and experiments on immiscible displacements in porous media. J. Fluid Mech. 189, 165–187.CrossRefGoogle Scholar
Lenormand, R., Zarcone, C. & Sarr, A. 1983 Mechanisms of the displacement of one fluid by another in a network of capillary ducts. J. Fluid Mech. 135, 337–353.CrossRefGoogle Scholar
Lister, J.R. & Kerr, R.C. 1991 Fluid-mechanical models of crack propagation and their application to magma transport in dykes. J. Geophys. Res. 96 (B6), 10049–10077.CrossRefGoogle Scholar
Lu, N.B., Browne, C.A., Amchin, D.B., Nunes, J.K. & Datta, S.S. 2019 Controlling capillary fingering using pore size gradients in disordered media. Phys. Rev. Fluids 4 (8), 084303.CrossRefGoogle Scholar
Luo, J., Zhu, Y., Guo, Q., Tan, L., Zhuang, Y., Liu, M., Zhang, C., Xiang, W. & Rohn, J. 2017 Experimental investigation of the hydraulic and heat-transfer properties of artificially fractured granite. Sci. Rep. 7 (1), 39882.CrossRefGoogle ScholarPubMed
Menand, T. & Tait, S.R. 2002 The propagation of a buoyant liquid-filled fissure from a source under constant pressure: an experimental approach. J. Geophys. Res. 107 (B11), ECV 16-1-ECV 16–14.CrossRefGoogle Scholar
Möri, A. & Lecampion, B. 2021 Arrest of a radial hydraulic fracture upon shut-in of the injection. Intl J. Solids Struct. 219, 151–165.CrossRefGoogle Scholar
Moukhtari, F.-E. & Lecampion, B. 2018 A semi-infinite hydraulic fracture driven by a shear-thinning fluid. J. Fluid Mech. 838, 573–605.CrossRefGoogle Scholar
Murphy, H.D., Tester, J.W., Grigsby, C.O. & Potter, R.M. 1981 Energy extraction from fractured geothermal reservoirs in low-permeability crystalline rock. J. Geophys. Res. 86 (B8), 7145–7158.CrossRefGoogle Scholar
O'Keeffe, N.J., Huppert, H.E. & Linden, P.F. 2018 a Experimental exploration of fluid-driven cracks in brittle hydrogels. J. Fluid Mech. 844, 435–458.CrossRefGoogle Scholar
O'Keeffe, N.J. & Linden, P.F. 2017 Hydrogel as a medium for fluid-driven fracture study. Exp. Mech. 57 (9), 1483–1493.CrossRefGoogle Scholar
O'Keeffe, N.J., Zheng, Z., Huppert, H.E. & Linden, P.F. 2018 b Symmetric coalescence of two hydraulic fractures. Proc. Natl Acad. Sci. USA 115 (41), 10228–10232.CrossRefGoogle ScholarPubMed
Osiptsov, A.A. 2017 Fluid mechanics of hydraulic fracturing: a review. J. Petrol. Sci. Engng 156, 513–535.CrossRefGoogle Scholar
Parisio, F. & Yoshioka, K. 2020 Modeling fluid reinjection into an enhanced geothermal system. Geophys. Res. Lett. 47 (19), e2020GL089886.CrossRefGoogle Scholar
Park, C.-W. & Homsy, G.M. 1984 Two-phase displacement in Hele-Shaw cells: theory. J. Fluid Mech. 139, 291–308.CrossRefGoogle Scholar
Paterson, L. 1981 Radial fingering in a Hele-Shaw cell. J. Fluid Mech. 113 (1), 513–529.CrossRefGoogle Scholar
Peng, G.G., Pihler-Puzovic, D., Juel, A., Heil, M. & Lister, J.R. 2015 Displacement flows under elastic membranes. Part 2. Analysis of interfacial effects. J. Fluid Mech. 784, 512–547.CrossRefGoogle Scholar
Pihler-Puzović, D., Illien, P., Heil, M. & Juel, A. 2012 Suppression of complex fingerlike patterns at the interface between air and a viscous fluid by elastic membranes. Phys. Rev. Lett. 108 (7), 074502.CrossRefGoogle Scholar
Pihler-Puzović, D., Juel, A., Peng, G.G., Lister, J.R. & Heil, M. 2015 Displacement flows under elastic membranes. Part 1. Experiments and direct numerical simulations. J. Fluid Mech. 784, 487–511.CrossRefGoogle Scholar
Pihler-Puzović, D., Périllat, R., Russell, M., Juel, A. & Heil, M. 2013 Modelling the suppression of viscous fingering in elastic-walled Hele-Shaw cells. J. Fluid Mech. 731, 162–183.CrossRefGoogle Scholar
Primkulov, B.K., Pahlavan, A.A., Fu, X., Zhao, B., MacMinn, C.W. & Juanes, R. 2019 Signatures of fluid–fluid displacement in porous media: wettability, patterns and pressures. J. Fluid Mech. 875, R4.CrossRefGoogle Scholar
Primkulov, B.K., Pahlavan, A.A., Fu, X., Zhao, B., MacMinn, C.W. & Juanes, R. 2021 Wettability and Lenormand's diagram. J. Fluid Mech. 923, A34.CrossRefGoogle Scholar
Rice, J.R. 1968 Mathematical Analysis in the Mechanics of Fracture. Academic Press.Google Scholar
Rubin, A.M. 1995 Propagation of magma-filled cracks. Annu. Rev. Earth Planet. Sci. 23 (1), 287–336.CrossRefGoogle Scholar
Saffman, P.G. & Taylor, G.I. 1958 The penetration of a fluid into a porous medium or Hele-Shaw cell containing a more viscous liquid. Proc. R. Soc. Lond. A 245 (1242), 312–329.Google Scholar
Savitski, A.A. & Detournay, E. 2002 Propagation of a penny-shaped fluid-driven fracture in an impermeable rock: asymptotic solutions. Intl J. Solids Struct. 39 (26), 6311–6337.CrossRefGoogle Scholar
Sneddon, I.N. & Mott, N.F. 1946 The distribution of stress in the neighbourhood of a crack in an elastic solid. Proc. R. Soc. Lond. A 187 (1009), 229–260.Google Scholar
Spence, D.A. & Sharp, P. 1985 Self-similar solutions for elastohydrodynamic cavity flow. Proc. R. Soc. Lond. A 400 (1819), 289–313.Google Scholar
Stokes, J.P., Weitz, D.A., Gollub, J.P., Dougherty, A., Robbins, M.O., Chaikin, P.M. & Lindsay, H.M. 1986 Interfacial stability of immiscible displacement in a porous medium. Phys. Rev. Lett. 57 (14), 1718–1721.CrossRefGoogle Scholar
Tabeling, P., Zocchi, G. & Libchaber, A. 1987 An experimental study of the Saffman–Taylor instability. J. Fluid Mech. 177, 67–82.CrossRefGoogle Scholar
Takada, A. 1990 Experimental study on propagation of liquid-filled crack in gelatin: shape and velocity in hydrostatic stress condition. J. Geophys. Res. 95 (B6), 8471–8481.CrossRefGoogle Scholar
Tanveer, S. 1993 Evolution of Hele-Shaw interface for small surface tension. J. Geophys. Res. 343 (1668), 155–204.Google Scholar
Wang, J., Elsworth, D. & Denison, M.K. 2018 Propagation, proppant transport and the evolution of transport properties of hydraulic fractures. J. Fluid Mech. 855, 503–534.CrossRefGoogle Scholar
Yang, Z., Méheust, Y., Neuweiler, I., Hu, R., Niemi, A. & Chen, Y.-F. 2019 Modeling immiscible two-phase flow in rough fractures from capillary to viscous fingering. Water Resour. Res. 55 (3), 2033–2056.CrossRefGoogle Scholar
Zhao, B., MacMinn, C.W. & Juanes, R. 2016 Wettability control on multiphase flow in patterned microfluidics. Proc. Natl Acad. Sci. USA 113 (37), 10251–10256.CrossRefGoogle ScholarPubMed

Tanikella and Dressire supplementary movie 1

Time evolution of the pre-fracture formed in experiment 1. The red-dyed oil propagates radially and forms an axisymmetric fracture. The movie is accelerated 50 times.

Download Tanikella and Dressire supplementary movie 1(Video)
Video 11.5 MB

Tanikella and Dressire supplementary movie 2

Time evolution of the fracture formed in experiment 1. The black-dyed water is injected at the center of the pre-fracture. Both the fracture tip and the interface between the two fluids exhibit an axisymmetric propagation. The movie is accelerated 50 times.

Download Tanikella and Dressire supplementary movie 2(Video)
Video 38.4 MB