Article contents
Axisymmetric column collapses of bi-frictional granular mixtures
Published online by Cambridge University Press: 12 May 2023
Abstract
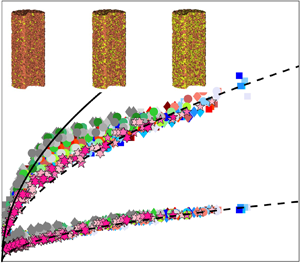
The behaviour of granular column collapses is associated with the dynamics of geohazards, such as debris flows, landslides and pyroclastic flows, yet their underlying physics is still not well understood. In this paper, we explore granular column collapses using the sphero-polyhedral discrete element method, where the system contains two types of particles with different frictional properties. We impose three different mixing ratios and multiple different particle frictional coefficients, which lead to different run-out distances and deposition heights. Based on our previous work and a simple mixture theory, we propose a new effective initial aspect ratio for the bi-frictional granular mixture, which helps unify the description of the relative run-out distances. We analyse the kinematics of bi-frictional granular column collapses and find that deviations from classical power-law scaling in both the dimensionless terminal time and the dimensionless time when the system reaches the maximum kinetic energy may result from differences in the initial solid fraction and initial structures. To clarify the influence of initial states, we further decrease the initial solid fraction of granular column collapses, and propose a trial function to quantitatively describe its influence. Due to the utilization of a simple mixture theory of contact occurrence probability, this study can be associated with the friction-dependent rheology of granular systems and friction-induced granular segregations, and further generalized to applications with multiple species of particles in various natural and engineering mixtures.
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
References
- 5
- Cited by



