Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-22T09:07:26.042Z Has data issue: false hasContentIssue false
  • English
  • Français

Axially homogeneous Rayleigh–Bénard convection in a cylindrical cell

Published online by Cambridge University Press:  01 December 2011

Laura E. Schmidt ,
Enrico Calzavarini ,
Detlef Lohse ,
Federico Toschi  and
Roberto Verzicco
Laura E. Schmidt
Affiliation:
Physics of Fluids, Department of Science and Technology, Impact and Mesa+ Institutes, and J. M. Burgers Center for Fluid Dynamics, University of Twente, PO Box 217, 7500 AE Enschede, The Netherlands
Enrico Calzavarini*
Affiliation:
Laboratoire de Mécanique de Lille, CNRS/UMR 8107, Université Lille 1, and Polytech’Lille, Cité Scientifique, Avenue P. Langevin, 59650 Villeneuve d’Ascq, France
Detlef Lohse
Affiliation:
Physics of Fluids, Department of Science and Technology, Impact and Mesa+ Institutes, and J. M. Burgers Center for Fluid Dynamics, University of Twente, PO Box 217, 7500 AE Enschede, The Netherlands
Federico Toschi
Affiliation:
Department of Physics, and Department of Mathematics and Computer Science, and J. M. Burgers Center for Fluid Dynamics, Eindhoven University of Technology, 5600 MB Eindhoven, The Netherlands CNR-IAC, Via dei Taurini 19, 00185 Rome, Italy
Roberto Verzicco
Affiliation:
Physics of Fluids, Department of Science and Technology, Impact and Mesa+ Institutes, and J. M. Burgers Center for Fluid Dynamics, University of Twente, PO Box 217, 7500 AE Enschede, The Netherlands Department of Mechanical Engineering, University of Rome ‘Tor Vergata’, Via del Politecnico 1, 00133 Rome, Italy
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Previous numerical studies have shown that the ‘ultimate regime of thermal convection’ can be attained in a Rayleigh–Bénard cell when the kinetic and thermal boundary layers are eliminated by replacing both lateral and horizontal walls with periodic boundary conditions (homogeneous Rayleigh–Bénard convection). Then, the heat transfer scales like 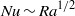and turbulence intensity as 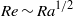, where the Rayleigh number 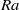indicates the strength of the driving force (for fixed values of 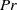, which is the ratio between kinematic viscosity and thermal diffusivity). However, experiments never operate in unbounded domains and it is important to understand how confinement might alter the approach to this ultimate regime. Here we consider homogeneous Rayleigh–Bénard convection in a laterally confined geometry – a small-aspect-ratio vertical cylindrical cell – and show evidence of the ultimate regime as 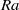is increased: in spite of the lateral confinement and the resulting kinetic boundary layers, we still find 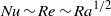at 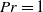. Further, it is shown that the system supports solutions composed of modes of exponentially growing vertical velocity and temperature fields, with 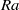as the critical parameter determining the properties of these modes. Counter-intuitively, in the low- 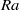regime, or for very narrow cylinders, the numerical simulations are susceptible to these solutions, which can dominate the dynamics and lead to very high and unsteady heat transfer. As 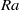is increased, interaction between modes stabilizes the system, evidenced by the increasing homogeneity and reduced fluctuations in the root-mean-square velocity and temperature fields. We also test that physical results become independent of the periodicity length of the cylinder, a purely numerical parameter, as the aspect ratio is increased.

JFM classification

Convection: Buoyancy-driven instability Turbulent Flows: Turbulent convection
Type
Papers
Information
Journal of Fluid Mechanics , Volume 691 , 25 January 2012 , pp. 52 - 68
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Ahlers, G., Grossmann, S. & Lohse, D. 2009 Heat transfer and large scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81, 503.CrossRefGoogle Scholar
2. Arakeri, J. H., Avila, F. E., Dada, J. M. & Tovar, R. O. 2000 Convection in a long vertical tube due to unstable stratification – a new type of turbulent flow? Curr. Sci. 79 (6), 859–866.Google Scholar
3. Batchelor, G. K. & Nitsche, J. M. 1991 Instability of stationary unbounded stratified fluid. J. Fluid Mech. 227, 357–391.CrossRefGoogle Scholar
4. Batchelor, G. K. & Nitsche, J. M. 1993 Instability of stratified fluid in a vertical cylinder. J. Fluid Mech. 252, 419–448.CrossRefGoogle Scholar
5. Biferale, L., Calzavarini, E., Toschi, F. & Tripiccione, R. 2003 Universality of anisotropic fluctuations from numerical simulations of turbulent flows. Europhys. Lett. 64 (4), 461–467.CrossRefGoogle Scholar
6. Calzavarini, E., Doering, C. R., Gibbon, J. D., Lohse, D., Tanabe, A. & Toschi, F. 2006 Exponentially growing solutions of homogeneous Rayleigh–Bénard flow. Phys. Rev. E 73, R035301.CrossRefGoogle Scholar
7. Calzavarini, E., Lohse, D., Toschi, F. & Tripiccione, R. 2005 Rayleigh and Prandtl number scaling in the bulk of Rayleigh–Bénard turbulence. Phys. Fluids 17, 055107.CrossRefGoogle Scholar
8. Celani, A., Mazzino, A., Seminara, A. & Tizzi, M. 2007 Droplet condensation in two-dimensional Bolgiano turbulence. J. Turbul. 8, 1–9.CrossRefGoogle Scholar
9. Chavanne, X., Chilla, F., Castaing, B., Hebral, B., Chabaud, B. & Chaussy, J. 1997 Observation of the ultimate regime in Rayleigh–Bénard convection. Phys. Rev. Lett. 79, 3648–3651.CrossRefGoogle Scholar
10. Chavanne, X., Chilla, F., Chabaud, B., Castaing, B. & Hebral, B. 2001 Turbulent Rayleigh–Bénard convection in gaseous and liquid He. Phys. Fluids 13, 1300–1320.CrossRefGoogle Scholar
11. Cholemari, M. & Arakeri, J. 2005 Experiments and a model of turbulent exchange flow in a vertical pipe. Intl J. Heat Mass Transfer 48 (21–22), 4467–4473.CrossRefGoogle Scholar
12. Cholemari, M. & Arakeri, J. 2009 Axially homogeneous, zero mean flow buoyancy-driven turbulence in a vertical pipe. J. Fluid Mech. 621, 69–102.CrossRefGoogle Scholar
13. Dubrulle, B. 2001 Momentum transport and torque scaling in Taylor–Couette flow from an analogy with turbulent convection. Eur. Phys. J. B 21, 295.Google Scholar
14. Garaud, P., Ogilvie, G., Miller, N. & Stellmach, S. 2010 A model of the entropy flux and Reynolds stress in turbulent convection. Mon. Not. R. Astron. Soc. 407, 2451–2467.CrossRefGoogle Scholar
15. Gibert, M., Pabiou, H., Chilla, F. & Castaing, B. 2006 High-Rayleigh-number convection in a vertical channel. Phys. Rev. Lett. 96, 084501.CrossRefGoogle Scholar
16. Gibert, M., Pabiou, H., Tisserand, J.-C., Gertjerenken, B., Castaing, B. & Chillà, F. 2009 Heat convection in a vertical channel: plumes versus turbulence diffusion. Phys. Fluids 21, 035109.CrossRefGoogle Scholar
17. van Gils, D., Huisman, S. G., Bruggert, G. W., Sun, C. & Lohse, D. 2011 Torque scaling in turbulent Taylor–Couette flow with co- and counter-rotating cylinders. Phys. Rev. Lett. 106, 024502.CrossRefGoogle Scholar
18. Grossmann, S. & Lohse, D. 2000 Scaling in thermal convection: a unifying theory. J. Fluid Mech. 407, 27–56.CrossRefGoogle Scholar
19. Grossmann, S. & Lohse, D. 2001 Thermal convection for large Prandtl number. Phys. Rev. Lett. 86, 3316–3319.CrossRefGoogle Scholar
20. Grossmann, S. & Lohse, D. 2002 Prandtl and Rayleigh number dependence of the Reynolds number in turbulent thermal convection. Phys. Rev. E 66, 016305.CrossRefGoogle ScholarPubMed
21. Grossmann, S. & Lohse, D. 2011 Multiple scaling in the ultimate regime of thermal convection. Phys. Fluids 23, 045108.CrossRefGoogle Scholar
22. Halesa, L. 1937 Convection currents in geysers. Mon. Not. R. Astron. Soc. Geophys. Suppl. 4, 122.Google Scholar
23. Jones, C. A. & Moore, D. R. 1979 The stability of axisymmetric convection. Geophys. Astrophys. Fluid Dyn. 11, 245–270.CrossRefGoogle Scholar
24. Kadanoff, L. P. 2001 Turbulent heat flow: structures and scaling. Phys. Today 54 (8), 34–39.CrossRefGoogle Scholar
25. Kim, J. & Moin, P. 1985 Application of a fractional-step method to incompressible Navier–Stokes equations. J. Comput. Phys. 59, 308–323.CrossRefGoogle Scholar
26. Kraichnan, R. H. 1962 Turbulent thermal convection at arbritrary Prandtl number. Phys. Fluids 5, 1374–1389.CrossRefGoogle Scholar
27. Landau, L. D. & Lifshitz, E. M. 1987 Fluid Mechanics. Pergamon.Google Scholar
28. Lohse, D. & Toschi, F. 2003 The ultimate state of thermal convection. Phys. Rev. Lett. 90, 034502.CrossRefGoogle ScholarPubMed
29. Lohse, D. & Xia, K.-Q. 2010 Small-scale properties of turbulent Rayleigh–Bénard convection. Annu. Rev. Fluid Mech. 42, 335–364.CrossRefGoogle Scholar
30. Perrier, F., Morat, P. & LeMouel, J. L. 2002 Dynamics of air avalanches in the access pit of an underground quarry. Phys. Rev. Lett. 89, 134501.CrossRefGoogle ScholarPubMed
31. Siggia, E. D. 1994 High Rayleigh number convection. Annu. Rev. Fluid Mech. 26, 137–168.CrossRefGoogle Scholar
32. Simitev, R. D. & Busse, F. H. 2010 Problems of astrophysical turbulent convection: thermal convection in a layer without boundaries. In Center for Turbulence Research, Proceedings of the Summer Program, 2010, Stanford University, CA (ed. Parviz Moin, Johan Larsson & Nagi Mansour), website where the proccedings can be found:http://www.stanford.edu/group/ctr/Summer/SP10/.Google Scholar
33. Spiegel, E. A. 1971 Convection in stars. Annu. Rev. Astron. Astrophys. 9, 323–352.CrossRefGoogle Scholar
34. Taylor, G. I. 1954 Diffusion and mass transport in tubes. Proc. Phys. Soc. B 67, 857–869.CrossRefGoogle Scholar
35. Tisserand, J.-C., Creyssels, M., Gibert, M., Castaing, D. & Chillà, F. 2010 Convection in a vertical channel. New J. Phys. 12, 075024.CrossRefGoogle Scholar
36. Verzicco, R. & Camussi, R. 2003 Numerical experiments on strongly turbulent thermal convection in a slender cylindrical cell. J. Fluid Mech. 477, 19–49.CrossRefGoogle Scholar
37. Verzicco, R. & Orlandi, P. 1996 A finite-difference scheme for three-dimensional incompressible flow in cylindrical coordinates. J. Comput. Phys. 123, 402–413.CrossRefGoogle Scholar

Schmidt et al. supplementary material

Destabilization of the growing dipolar mode: Instantaneous contour plots of the dimensionless vertical velocity w through a vertical cross-section of the cell, for Rayleigh $Ra=7.66 \cdot 10^{3}$, Prandtl Pr = 1 and Aspect-ratio $\Gamma = 1/2$. The color scale is varied according to the flow so that the structures can be seen at all times.

Download Schmidt et al. supplementary material(Video)
Video 1.2 MB

Schmidt et al. supplementary material

Destabilization of the growing dipolar mode: Instantaneous contour plots of the dimensionless vertical velocity w through a vertical cross-section of the cell, for Rayleigh $Ra=7.66 \cdot 10^{3}$, Prandtl Pr = 1 and Aspect-ratio $\Gamma = 1/2$. The color scale is varied according to the flow so that the structures can be seen at all times.

Download Schmidt et al. supplementary material(Video)
Video 1.7 MB