Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-12-02T22:00:33.708Z Has data issue: false hasContentIssue false
  • English
  • Français

Available potential vorticity and wave-averaged quasi-geostrophic flow

Published online by Cambridge University Press:  23 November 2015

G. L. Wagner Open the ORCID record for G. L. Wagner [Opens in a new window]  and
W. R. Young
G. L. Wagner*
Affiliation:
Department of Mechanical and Aerospace Engineering, University of California San Diego, La Jolla, CA 92093-0411, USA
W. R. Young
Affiliation:
Scripps Institution of Oceanography, University of California San Diego, La Jolla, CA 92023-0213, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We derive a wave-averaged potential vorticity equation describing the evolution of strongly stratified, rapidly rotating quasi-geostrophic (QG) flow in a field of inertia-gravity internal waves. The derivation relies on a multiple-time-scale asymptotic expansion of the Eulerian Boussinesq equations. Our result confirms and extends the theory of Bühler & McIntyre (J. Fluid Mech., vol. 354, 1998, pp. 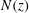609–646) to non-uniform stratification with buoyancy frequency $N(z)$ and therefore non-uniform background potential vorticity 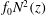$f_{0}N^{2}(z)$, and does not require spatial-scale separation between waves and balanced flow. Our interest in non-uniform background potential vorticity motivates the introduction of a new quantity: ‘available potential vorticity’ (APV). Like Ertel potential vorticity, APV is exactly conserved on fluid particles. But unlike Ertel potential vorticity, linear internal waves have no signature in the Eulerian APV field, and the standard QG potential vorticity is a simple truncation of APV for low Rossby number. The definition of APV exactly eliminates the Ertel potential vorticity signal associated with advection of a non-uniform background state, thereby isolating the part of Ertel potential vorticity available for balanced-flow evolution. The effect of internal waves on QG flow is expressed concisely in a wave-averaged contribution to the materially conserved QG potential vorticity. We apply the theory by computing the wave-induced QG flow for a vertically propagating wave packet and a mode-one wave field, both in vertically bounded domains.

JFM classification

Geophysical and Geological Flows: Geophysical and Geological Flows Geophysical and Geological Flows: Internal waves Geophysical and Geological Flows: Quasi-geostrophic flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 785 , 25 December 2015 , pp. 401 - 424
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andrews, D. G. & McIntyre, M. E. 1978 An exact theory of nonlinear waves on a Lagrangian-mean flow. J. Fluid Mech. 89, 609–646.CrossRefGoogle Scholar
Bretherton, F. P. 1969 On the mean motion induced by internal gravity waves. J. Fluid Mech. 36 (4), 785–803.Google Scholar
Bühler, O. 2009 Waves and Mean Flows. Cambridge University Press.Google Scholar
Bühler, O. & McIntyre, M. E. 1998 On non-dissipative wave-mean interactions in the atmosphere or oceans. J. Fluid Mech. 354, 609–646.Google Scholar
Callies, J., Ferrari, R. & Bühler, O. 2014 Transition from geostrophic turbulence to inertia–gravity waves in the atmospheric energy spectrum. Proc. Natl Acad. Sci. USA 111 (48), 17033–17038.CrossRefGoogle ScholarPubMed
Craik, A. D. 1988 Wave Interactions and Fluid Flows. Cambridge University Press.Google Scholar
Holliday, D. & McIntyre, M. E. 1981 On potential energy density in an incompressible, stratified fluid. J. Fluid Mech. 107, 221–225.CrossRefGoogle Scholar
Holmes-Cerfon, M., Bühler, O. & Ferrari, R. 2011 Particle dispersion by random waves in the rotating Boussinesq system. J. Fluid Mech. 670, 150–175.Google Scholar
Kataoka, T. & Akylas, T. 2015 On three-dimensional internal gravity wave beams and induced large-scale mean flows. J. Fluid Mech. 769, 621–634.Google Scholar
McIntyre, M. 1988 A note on the divergence effect and the Lagrangian-mean surface elevation in periodic water waves. J. Fluid Mech. 189, 235–242.Google Scholar
Müller, P., Holloway, G., Henyey, F. & Pomphrey, N. 1986 Nonlinear interactions among internal gravity waves. Rev. Geophys. 24 (3), 493–536.Google Scholar
Pedlosky, J. 1982 Geophysical Fluid Dynamics. Springer.Google Scholar
Reznik, G., Zeitlin, V. & Ben Jelloul, M. 2001 Nonlinear theory of geostrophic adjustment. Part 1. Rotating shallow-water model. J. Fluid Mech. 445, 93–120.CrossRefGoogle Scholar
Salmon, R. 1998 Lectures on Geophysical Fluid Dynamics. Oxford University Press.Google Scholar
Vallis, G. K. 2006 Atmospheric and Oceanic Fluid Dynamics: Fundamentals and Large-Scale Circulation. Cambridge University Press.Google Scholar
Vanneste, J. 2013 Balance and spontaneous wave generation in geophysical flows. Annu. Rev. Fluid Mech. 45, 147–172.Google Scholar
Xie, J.-H. & Vanneste, J. 2015 A generalised Lagrangian-mean model of the interactions between near-inertial waves and mean flow. J. Fluid Mech. 774, 143–169.Google Scholar
Zeitlin, V., Reznik, G. & Ben Jelloul, M. 2003 Nonlinear theory of geostrophic adjustment. Part 2. Two-layer and continuously stratified primitive equations. J. Fluid Mech. 491, 207–228.Google Scholar