Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Zubarev, N. M.
and
Karabut, E. A.
2018.
Exact Local Solutions for the Formation of Singularities on the Free Surface of an Ideal Fluid.
JETP Letters,
Vol. 107,
Issue. 7,
p.
412.
Childress, Stephen
and
Gilbert, Andrew D
2018.
Eroding dipoles and vorticity growth for Euler flows in ${{\mathbb{R}}}^{3}$: the hairpin geometry as a model for finite-time blowup.
Fluid Dynamics Research,
Vol. 50,
Issue. 1,
p.
011418.
Agafontsev, D. S.
Kuznetsov, E. A.
and
Mailybaev, A. A.
2018.
Development of high vorticity structures and geometrical properties of the vortex line representation.
Physics of Fluids,
Vol. 30,
Issue. 9,
Campolina, Ciro S.
and
Mailybaev, Alexei A.
2018.
Chaotic Blowup in the 3D Incompressible Euler Equations on a Logarithmic Lattice.
Physical Review Letters,
Vol. 121,
Issue. 6,
Agafontsev, D. S.
Kuznetsov, E. A.
and
Mailybaev, A. A.
2019.
Statistical Properties of the Velocity Field for the 3D Hydrodynamic Turbulence Onset.
JETP Letters,
Vol. 110,
Issue. 2,
p.
121.
Agafontsev, D S
Kuznetsov, E A
and
Mailybaev, A A
2019.
Compressible structures in incompressible hydrodynamics and their role in turbulence onset.
IOP Conference Series: Earth and Environmental Science,
Vol. 231,
Issue. ,
p.
012002.
Chefranov, S G
and
Chefranov, A S
2019.
Exact solution of the compressible Euler–Helmholtz equation and the millennium prize problem generalization.
Physica Scripta,
Vol. 94,
Issue. 5,
p.
054001.
Agélas, Léo
2019.
A new path to the non blow-up of incompressible flows.
Annales de l'Institut Henri Poincaré C, Analyse non linéaire,
Vol. 36,
Issue. 6,
p.
1503.
Dubrulle, Bérengère
2019.
Beyond Kolmogorov cascades.
Journal of Fluid Mechanics,
Vol. 867,
Issue. ,
Childress, Stephen
and
Gilbert, Andrew D
2020.
A filamentary cascade model of the inertial range.
Fluid Dynamics Research,
Vol. 52,
Issue. 3,
p.
035502.
Kuznetsov, E. A.
and
Mikhailov, E. A.
2020.
Notes on Collapse in Magnetic Hydrodynamics.
Journal of Experimental and Theoretical Physics,
Vol. 131,
Issue. 3,
p.
496.
Campolina, Ciro S
and
Mailybaev, Alexei A
2021.
Fluid dynamics on logarithmic lattices.
Nonlinearity,
Vol. 34,
Issue. 7,
p.
4684.
Agafontsev, D. S.
Kuznetsov, E. A.
and
Mailybaev, A. A.
2021.
Stability of Tangential Discontinuity for the Vortex Pancakes.
JETP Letters,
Vol. 114,
Issue. 2,
p.
71.
Kuznetsov, E.A.
and
Mikhailov, E.A.
2022.
Slipping flows and their breaking.
Annals of Physics,
Vol. 447,
Issue. ,
p.
169088.
Agafontsev, D S
Kuznetsov, E A
Mailybaev, A A
and
Sereshchenko, E V
2022.
Compressible vortex structures and their role in the onset of hydrodynamic turbulence.
Physics-Uspekhi,
Vol. 65,
Issue. 2,
p.
189.
Li, Y.
Li, Q.
Wang, Y.
Chen, J.
and
Cai, W.-H.
2022.
Optimization of a Zigzag-channel printed circuit heat exchanger for supercritical methane flow.
Cryogenics,
Vol. 121,
Issue. ,
p.
103415.
Kuznetsov, E. A.
Mikhailov, E. A.
and
Serdyukov, M. G.
2023.
Nonlinear Dynamics of Slipping Flows.
Radiophysics and Quantum Electronics,
Vol. 66,
Issue. 2-3,
p.
129.
Krstulovic, Giorgio
and
Nazarenko, Sergey
2024.
Initial evolution of three-dimensional turbulence en route to the Kolmogorov state: Emergence and transformations of coherent structures, self-similarity, and instabilities.
Physical Review Fluids,
Vol. 9,
Issue. 3,
Meng, Zhaoyuan
and
Yang, Yue
2024.
Lagrangian dynamics and regularity of the spin Euler equation.
Journal of Fluid Mechanics,
Vol. 985,
Issue. ,
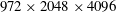 $972\times 2048\times 4096$.
$972\times 2048\times 4096$.