Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Goddard, J. D.
and
Acrivos, Andreas
1966.
Asymptotic expansions for laminar forced-convection heat and mass transfer Part 2. Boundary-layer flows.
Journal of Fluid Mechanics,
Vol. 24,
Issue. 2,
p.
339.
Eckert, E.R.G.
Sparrow, E.M.
Ibele, W.E.
and
Goldstein, R.J.
1966.
Heat transfer—A review of current literature.
International Journal of Heat and Mass Transfer,
Vol. 9,
Issue. 7,
p.
599.
Brenner, Howard
1966.
Advances in Chemical Engineering Volume 6.
Vol. 6,
Issue. ,
p.
287.
Ping Huei Sih
and
Newman, John
1967.
Mass transfer to the rear of a sphere in Stokes flow.
International Journal of Heat and Mass Transfer,
Vol. 10,
Issue. 12,
p.
1749.
Yu-Fang, Pan
and
Acrivos, Andreas
1968.
Heat transfer at high péclet number in regions of closed streamlines.
International Journal of Heat and Mass Transfer,
Vol. 11,
Issue. 3,
p.
439.
Condiff, D. W.
and
Brenner, H.
1969.
Transport Mechanics in Systems of Orientable Particles.
The Physics of Fluids,
Vol. 12,
Issue. 3,
p.
539.
Brenner, Howard
1970.
Orientation-space boundary layers in problems of rotational diffusion and convection at large rotary Péclet numbers.
Journal of Colloid and Interface Science,
Vol. 34,
Issue. 1,
p.
103.
Robertson, C. R.
and
Acrivos, A.
1970.
Low Reynolds number shear flow past a rotating circular cylinder. Part 2. Heat transfer.
Journal of Fluid Mechanics,
Vol. 40,
Issue. 04,
p.
705.
Nunge, Richard J.
Porta, Earnest W.
and
Bentley, Ronald
1970.
A correlation of local nusselt numbers for laminar flow heat transfer in annuli.
International Journal of Heat and Mass Transfer,
Vol. 13,
Issue. 5,
p.
927.
MASLIYAH, JACOB H.
and
EPSTEIN, NORMAN
1972.
Proceedings of the International Symposium on Two-Phase Systems.
p.
613.
Caswell, Bruce
1972.
The stability of particle motion near a wall in Newtonian and non-Newtonian fluids.
Chemical Engineering Science,
Vol. 27,
Issue. 2,
p.
373.
BRENNER, HOWARD
1972.
Proceedings of the International Symposium on Two-Phase Systems.
p.
509.
1972.
The Method of Weighted Residuals and Variational Principles - With Application in Fluid Mechanics, Heat and Mass Transfer.
Vol. 87,
Issue. ,
p.
15.
Avudainayagam, A.
1972.
Heat transfer from a slowly rotating sphere.
Applied Scientific Research,
Vol. 26,
Issue. 1,
p.
18.
Homsy, Robert V.
and
Newman, John
1973.
Mass transfer to a plane below a rotating disk at high Schmidt numbers.
AIChE Journal,
Vol. 19,
Issue. 5,
p.
929.
K. Sirkar, Kamalesh
1974.
Creeping flow mass transfer to a single active sphere in a random spherical inactive particle cloud at high schmidt numbers.
Chemical Engineering Science,
Vol. 29,
Issue. 3,
p.
863.
Bogolyubov, Yu. E.
Geshev, P. I.
Nakoryakov, V. E.
and
Ogorodnikov, I. A.
1974.
Theory of the electrical diffusion measurement of the spectral characteristics of a turbulent flow.
Journal of Applied Mechanics and Technical Physics,
Vol. 13,
Issue. 4,
p.
528.
Abramzon, B. M.
Rivkind, V. Ya.
and
Fishbein, G. A.
1976.
Unsteady mass transfer with a heterogeneous chemical reaction during laminar flow past a sphere.
Journal of Engineering Physics,
Vol. 30,
Issue. 1,
p.
52.
Gupalo, Iu.P.
Polianin, A.D.
and
Riazantsev, Iu.S.
1976.
Diffusion to a particle at large péclet numbers in the case of arbitrary axisymmetric flow over a viscous fluid.
Journal of Applied Mathematics and Mechanics,
Vol. 40,
Issue. 5,
p.
893.
Tardos, G. I.
Gutfinger, Chiam
and
Abuaf, Nesim
1976.
High peclet number mass transfer to a sphere in a fixed or fluidized bed.
AIChE Journal,
Vol. 22,
Issue. 6,
p.
1147.
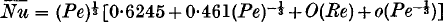
 and Pe are based on the radius of the sphere.
and Pe are based on the radius of the sphere.

