Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-28T17:38:24.990Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotic expansion of the velocity field within the front of viscoplastic surges: comparison with experiments

Published online by Cambridge University Press:  17 December 2019

G. Chambon Open the ORCID record for G. Chambon [Opens in a new window] ,
P. Freydier ,
M. Naaim  and
J.-P. Vila
G. Chambon*
Affiliation:
Univ. Grenoble Alpes, INRAE, ETNA, F-38402Saint-Martin-d’Hères, France
P. Freydier
Affiliation:
Univ. Grenoble Alpes, INRAE, ETNA, F-38402Saint-Martin-d’Hères, France Laboratoire FAST, Univ. Paris Sud, CNRS, Univ. Paris-Saclay, F-91405Orsay, France
M. Naaim
Affiliation:
Univ. Grenoble Alpes, INRAE, ETNA, F-38402Saint-Martin-d’Hères, France
J.-P. Vila
Affiliation:
Institut de Mathématiques de Toulouse, UMR 5219, Univ. Toulouse, CNRS, INSA, F-31077Toulouse, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this article, we investigate the internal dynamics (velocity profiles and shear rate) of free-surface surges made of viscoplastic fluids. Compared with fluids without a yield stress, additional complexity arises from the possible coexistence of sheared and unsheared (or pseudo-plug) zones in the flow. Expanding on the thin-layer approach of Fernandez-Nieto et al. (J. Non-Newtonian Fluid Mech., vol. 165, 2010, pp. 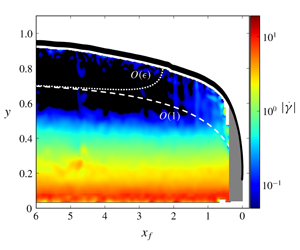712–732), we derive formal asymptotic expansions of the velocity field and discharge up to $O(\unicode[STIX]{x1D716})$ with respect to flow aspect ratio $\unicode[STIX]{x1D716}$. Detailed comparisons between these theoretical predictions and experimental data reveal that, although the leading-order approximation (equivalent to a lubrication model) satisfactorily accounts for the global dynamics of the flow, considering $O(\unicode[STIX]{x1D716})$ correction terms is required to capture the evolution of velocity and shear rate close to the tip. Notably, these correction terms are responsible for the vanishing of the unsheared layer in the tip region, a feature clearly observed in the experiments. Differences between the leading-order and $O(\unicode[STIX]{x1D716})$ models appear to be enhanced by the viscoplastic character of the fluid. In particular, $O(\unicode[STIX]{x1D716})$ correction terms related to the existence of $O(1)$ plastic normal stresses in the pseudo-plug layer play a critical role. This study provides important insights for future development of consistent shallow-water models adapted to viscoplastic materials.

JFM classification

Low-Reynolds-number flows: Lubrication theory
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 884 , 10 February 2020 , A43
Copyright
© 2019 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Amaouche, M., Djema, A. & Ait Aberrahmane, H. 2012 Film flow for power-law fluids: modeling and linear stability. Eur. J. Mech. (B/Fluids) 34, 70–84.CrossRefGoogle Scholar
Ancey, C. 2007 Plasticity and geophysical flows: a review. J. Non-Newtonian. Fluid Mech. 142, 4–35.CrossRefGoogle Scholar
Ancey, C., Andreini, N. & Epely-Chauvin, G. 2012 Viscoplastic dambreak waves: review of simple computational approaches and comparison with experiments. Adv. Water Res. 48, 79–91.CrossRefGoogle Scholar
Ancey, C. & Cochard, S. 2009 The dam-break problem for Herschel–Bulkley viscoplastic fluids down steep flumes. J. Non-Newtonian. Fluid Mech. 158, 18–35.CrossRefGoogle Scholar
Ancey, C., Cochard, S. & Andreini, N. 2009 The dam-break problem for viscous fluids in the high-capillary-number limit. J. Fluid Mech. 624, 1–22.CrossRefGoogle Scholar
Ancey, C., Cochard, S., Rentschler, M. & Wiederseiner, S. 2007 Existence and features of similarity solutions for non-Boussinesq gravity currents. Physica D 226, 32–54.CrossRefGoogle Scholar
Andreini, N., Epely-Chauvin, G. & Ancey, C. 2012 Internal dynamics of Newtonian and viscoplastic fluid avalanches down a sloping bed. Phys. Fluids 24, 053101.CrossRefGoogle Scholar
Balmforth, N. J. & Craster, R. V. 1999 A consistent thin-layer theory for Bingham plastics. J. Non-Newtonian. Fluid Mech. 84, 65–81.CrossRefGoogle Scholar
Balmforth, N. J., Craster, R. V., Rust, A. C. & Sassi, R. 2006 Viscoplastic flow over an inclined surface. J. Non-Newtonian. Fluid Mech. 139, 103–127.CrossRefGoogle Scholar
Balmforth, N. J., Frigaard, I. A. & Ovarlez, G. 2014 Yielding to stress: recent developments in viscoplastic fluid mechanics. Annu. Rev. Fluid Mech. 46, 121–146.CrossRefGoogle Scholar
Balmforth, N. J. & Liu, J. J. 2004 Roll waves in mud. J. Fluid Mech. 519, 33–54.CrossRefGoogle Scholar
Benney, D. J. 1966 Long waves on liquid films. J. Math. Phys. 45, 150–155.CrossRefGoogle Scholar
Bernabeu, N., Saramito, P. & Smutek, C. 2014 Numerical modeling of non-Newtonian viscoplastic flows: Part II. Viscoplastic fluids and general tridimensional topographies. Intl J. Numer. Anal. Model. 11, 213–228.Google Scholar
Bonn, D., Denn, M. M., Berthier, L., Divoux, T. & Manneville, S. 2017 Yield stress materials in soft condensed matter. Rev. Mod. Phys. 86, 035005.Google Scholar
Boutounet, M., Monnier, J. & Vila, J.-P. 2016 Multi-regime shallow free surface laminar flow models for quasi-Newtonian fluids. Eur. J. Mech. (B/Fluids) 55, 182–206.CrossRefGoogle Scholar
Chambon, G., Ghemmour, A. & Laigle, D. 2009 Gravity-driven surges of a viscoplastic fluid: an experimental study. J. Non-Newtonian. Fluid Mech. 158, 54–62.CrossRefGoogle Scholar
Chambon, G., Ghemmour, A. & Naaim, M. 2014 Experimental investigation of viscoplastic free-surface flows in steady uniform regime. J. Fluid Mech. 754, 332–364.CrossRefGoogle Scholar
Chanson, N. 2004 The Hydraulics of Open Channel Flow: An Introduction, 2nd edn. Elsevier.Google Scholar
Coussot, P. 1994 Steady, laminar, flow of concentrated mud suspensions in open channel. J. Hydraul Res. 32, 535–559.CrossRefGoogle Scholar
Coussot, P. 2014 Yield stress fluid flows: a review of experimental data. J. Non-Newtonian. Fluid Mech. 211, 31–49.CrossRefGoogle Scholar
Dussan V, E. B. 1976 The moving contact line: the slip boundary condition. J. Fluid Mech. 77, 665–684.CrossRefGoogle Scholar
Fernandez-Nieto, E. D., Noble, P. & Vila, J. P. 2010 Shallow water equations for non-Newtonian fluids. J. Non-Newtonian. Fluid Mech. 165, 712–732.CrossRefGoogle Scholar
Freydier, P., Chambon, G. & Naaim, M. 2017 Experimental characterization of velocity fields within the front of viscoplastic surges down an incline. J. Non-Newtonian. Fluid Mech. 240, 56–69.CrossRefGoogle Scholar
Frigaard, I., Paso, K. G. & de Souza Mendes, P. R. 2017 Bingham’s model in the oil and gas industry. Rheol. Acta 56, 259–282.CrossRefGoogle Scholar
Hogg, A. J. & Pritchard, D. 2004 The effects of hydraulic resistance on dam-break and other shallow inertial flows. J. Fluid Mech. 501, 179–212.CrossRefGoogle Scholar
Huang, X. & Garcia, M. H. 1998 A Herschel–Bulkley model for mud flow down a slope. J. Fluid Mech. 374, 305–333.CrossRefGoogle Scholar
Hunt, B. 1994 Newtonian fluid mechanics treatment of debris flows and avalanches. J. Hydraul. Engng 120, 1350–1363.CrossRefGoogle Scholar
Huppert, H. E. 2006 Gravity currents: a personal perspective. J. Fluid Mech. 554, 299–322.CrossRefGoogle Scholar
Iverson, R. M. 2013 Mechanics of debris flows and rock avalanches. In Handbook and Environmental Fluid Dynamics (ed. Fernando, H. J. S.), pp. 573–587. CRC Press/Taylor and Francis Group.Google Scholar
Kalliadasis, S., Ruyer-Quil, C., Scheid, B. & Velarde, M. G. 2012 Falling Liquid Films. Springer.CrossRefGoogle Scholar
Kirstetter, G., Hu, J., Delestre, O., Darboux, F., Lagrée, P.-Y., Popinet, S., Fullana, J. M. & Josserand, C. 2016 Modeling rain-driven overland flow: empirical versus analytical friction terms in the shallow water approximation. J. Hydrol. 536, 1–9.CrossRefGoogle Scholar
Laigle, D. & Coussot, P. 1997 Numerical modeling of mudflows. J. Hydraul. Engng 123, 617–623.CrossRefGoogle Scholar
Liu, K.-F. & Mei, C. C. 1994 Roll waves on a layer of a muddy fluid flowing down a gentle slope – a Bingham model. Phys. Fluids 6, 2577–2590.CrossRefGoogle Scholar
Liu, Y., Balmforth, N. J. & Hormozi, S. 2019 Viscoplastic surges down an incline. J. Non-Newtonian. Fluid Mech. 268, 1–11.CrossRefGoogle Scholar
Liu, Y., Balmforth, N. J., Hormozi, S. & Hewitt, D. R. 2016 Two-dimensional viscoplastic dambreaks. J. Non-Newtonian. Fluid Mech. 238, 65–79.CrossRefGoogle Scholar
Ng, C. O. & Mei, C. C. 1994 Roll waves on a shallow layer of mud modelled as a power-law fluid. J. Fluid Mech. 263, 151–183.CrossRefGoogle Scholar
Noble, P. & Vila, J.-P. 2013 Thin power-law film flow down an inclined plane: consistent shallow-water models and stability under large-scale perturbations. J. Fluid Mech. 735, 29–60.CrossRefGoogle Scholar
Piau, J. M. 1996 Flow of a yield stress fluid in a long domain. Application to flow on an inclined plane. J. Rheol. 40, 711–723.CrossRefGoogle Scholar
Piau, J. M. 2007 Carbopol gels: elastoviscoplastic and slippery glasses made of individual swollen sponges. Meso- and macroscopic properties, constitutive equations and scaling laws. J. Non-Newtonian. Fluid Mech. 144, 1–29.CrossRefGoogle Scholar
Richard, G. L., Ruyer-Quil, C. & Vila, J. P. 2016 A three-equation model for thin films down an inclined plane. J. Fluid Mech. 804, 162–200.CrossRefGoogle Scholar
Roussel, N. & Coussot, P. 2005 ‘Fyfty-cent rheometer’ for yield stress measurements: from slump to spreading flow. J. Rheol. 49, 705–718.CrossRefGoogle Scholar
Ruyer-Quil, C., Chakraborty, S. & Dandapat, B. S. 2012 Wavy regime of a power-law film flow. J. Fluid Mech. 692, 220–256.CrossRefGoogle Scholar
Ruyer-Quil, C. & Manneville, P. 1998 Modeling film flows down inclined planes. Eur. Phys. J. B 6, 277–292.CrossRefGoogle Scholar
Ruyer-Quil, C. & Manneville, P. 2000 Improved modeling of flows down inclined planes. Eur. Phys. J. B 15, 357–369.CrossRefGoogle Scholar
Saingier, G., Deboeuf, S. & Lagrée, P.-Y. 2016 On the front shape of an inertial granular flow down a rough incline. Phys. Fluids 28, 053302.CrossRefGoogle Scholar
Saint-Venant, A. J. C. B. de 1871 Théorie du mouvement non permanent des eaux, avec application aux crues des rivières et à l’introduction de marées dans leurs lits. C. R. Acad. Sci. Paris 73, 147–154 and 237–240.Google Scholar
Savage, S. B. & Hutter, K. 1989 The motion of a finite mass of granular material down a rough incline. J. Fluid Mech. 199, 177–215.CrossRefGoogle Scholar
Schellart, W. P. 2011 Rheology and density of glucose syrup and honey: determining their suitability for usage in analogue and fluid dynamic models of geological processes. J. Struct. Geol. 33, 1079–1088.CrossRefGoogle Scholar
Whitham, G. B. 1974 Linear and Nonlinear Waves. Wiley.Google Scholar