Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-25T01:47:38.808Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymmetries in the wake of a submarine model in pitch

Published online by Cambridge University Press:  15 June 2015

A. Ashok ,
T. Van Buren  and
A. J. Smits
A. Ashok*
Affiliation:
Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08540, USA
T. Van Buren
Affiliation:
Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08540, USA
A. J. Smits
Affiliation:
Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08540, USA Department of Mechanical and Aerospace Engineering, Monash University, VIC 3800, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

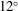Detailed velocity measurements in the wake of a body of revolution are reported for pitch angles up to $12^{\circ }$, over an unprecedented range of Reynolds numbers (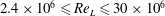$2.4\times 10^{6}\leqslant \mathit{Re}_{L}\leqslant 30\times 10^{6}$). The body of revolution, an idealized submarine shape (DARPA SUBOFF), is mounted using a support that mimics a semi-infinite sail. The wake measurements at all pitch angles and Reynolds numbers reveal the presence of a pair of streamwise vortices of unequal strengths which tend to rotate around each other as they evolve downstream. Various attempts to perturb the upstream conditions on the body had no significant impact on the relative strength of the vortices. In addition, two different models, tested in two different wind tunnels, show similar asymmetries, and we propose that wake asymmetry appears to be a robust feature of this flow, a result previously only seen for sharp-nosed bodies at high angles of attack. It is also shown that the wake behaviour for 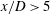$x/D>5$, in terms of the streamwise mean velocity and turbulence intensity distributions, appears to become invariant with Reynolds number for 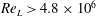$\mathit{Re}_{L}>4.8\times 10^{6}$.

JFM classification

Turbulent Flows: Turbulent Flows Vortex Flows: Vortex Flows Wakes/Jets: Wakes/Jets
Type
Papers
Information
Journal of Fluid Mechanics , Volume 774 , 10 July 2015 , pp. 416 - 442
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J. & Westerweel, J. 2011 Particle Image Velocimetry. Cambridge University Press.Google Scholar
Ashok, A., Bailey, S. C. C., Hultmark, M. & Smits, A. J. 2012 Hot-wire spatial resolution effects in measurements of grid-generated turbulence. Exp. Fluids 53 (6), 1713–1722.CrossRefGoogle Scholar
Ashok, A., Van Buren, T. & Smits, A. J. 2015 The turbulent wake of a submarine model in yaw. Exp. Fluids (in press) doi:10.1007/s00348-015-1997-4.CrossRefGoogle Scholar
Bippes, H. 1987 Boundary-Layer Separation: Experimental Investigation of Topological Structures in Three-dimensional Separated Flow. Springer.Google Scholar
Bradshaw, P. 1971 An Introduction to Turbulence and its Measurement. Pergamon.Google Scholar
Bridges, D. H. 2006 The asymmetric vortex wake problem – asking the right question. In 36th AIAA Fluid Dynamics Conference and Exhibit, Washington, DC, AIAA.Google Scholar
Bridges, D. H.2008 Estimate of the disturbance energy in an asymmetric vortex wake. In 38th Fluid Dynamics Conference and Exhibit. Seattle, Washington, DC, AIAA 2008-4180.Google Scholar
Bridges, D. H., Blanton, J. N., Brewer, W. H. & Park, J. T. 2003 Experimental investigation of the flow past a submarine at angle of drift. AIAA J. 41, 71–81.CrossRefGoogle Scholar
Chesnakas, C. & Simpson, R. L. 1997 Detailed investigation of the three-dimensional separation about a 6:1 prolate spheroid. AIAA J. 35 (6), 990–999.CrossRefGoogle Scholar
Feymark, A., Chapuid, M., Fureby, C. & Liefvendahl, M. 2012 Large eddy simulation of high Reynolds number partially separated flow. In 50th AIAA Aerospace Sciences Meeting, Washington, DC, AIAA.Google Scholar
Fu, T. C., Atsavapranee, P. & Hess, D. E.2002 PIV measurements of the cross-flow velocity field around a turning submarine model (ONR Body-1). Part I: experimental setup. Tech. Rep. Naval Surface Warfare Center Carderock Division.CrossRefGoogle Scholar
Fu, T. C., Shekarriz, A. & Huang, T. T. 1994 The flow structure in the lee of an inclined 6:1 prolate spheroid. J. Fluid Mech. 269, 79–106.CrossRefGoogle Scholar
Grandemange, M., Cadot, O. & Gohlke, M. 2012a Reflectional symmetry breaking of the separated flow over three-dimensional bluff bodies. Phys. Rev. E 86 (3), 035302.CrossRefGoogle ScholarPubMed
Grandemange, M., Gohlke, M. & Cadot, O. 2013 Turbulent wake past a three-dimensional blunt body. Part 1. Global modes and bi-stability. J. Fluid Mech. 722, 51–84.CrossRefGoogle Scholar
Grandemange, M., Gohlke, M. & Cadot, O. 2014 Turbulent wake past a three-dimensional blunt body. Part 2. Experimental sensitivity analysis. J. Fluid Mech. 752, 439–461.CrossRefGoogle Scholar
Grandemange, M., Gohlke, M., Parezanović, V. & Cadot, O. 2012b On experimental sensitivity analysis of the turbulent wake from an axisymmetric blunt trailing edge. Phys. Fluids 24 (3), 035106.CrossRefGoogle Scholar
Gregory, P. A., Joubert, P. N. & Chong, M. S.2004 Flow over a body of revolution in a steady turn. Tech. Rep. DSTO Platforms Sciences Laboratory.Google Scholar
Gregory, P. A., Joubert, P. N. & Chong, M. S. 2007 Measurements of turbulent crossflow separation created by a curved body of revolution. J. Fluid Mech. 589, 353–374.CrossRefGoogle Scholar
Groves, N. C., Huang, T. T. & Chang, M. S.1989 Geometric characteristics of DARPA SUBOFF models. Tech. Rep. David Taylor Research Centre.Google Scholar
Han, T. & Patel, V. C. 1979 Flow separation on a spheroid at incidence. J. Fluid Mech. 92, 643–657.CrossRefGoogle Scholar
Hess, D. E., Fu, T. C., Cubbage, S. J., Ratcliffe, T. J., Hoyt, J. G. III & Roddy, R. F. Jr. 2010 Naval maneuvering research and the need for shear stress measurements. In 48th AIAA Aerospace Sciences Meeting, Washington, DC, AIAA.Google Scholar
Hornung, H. & Perry, A. E. 1984 Some aspects of three-dimensional separation. Part I: streamsurface bifurcations. Z. Flugwiss. Weltraumforsch. 8 (2), 77–87.Google Scholar
Hosder, S. & Simpson, R. L. 2007 Experimental investigation of unsteady flow separation on a maneuvering axisymmetric body. J. Aircraft 44 (4), 1286–1295.CrossRefGoogle Scholar
Hultmark, M. & Smits, A. J. 2010 A note on temperature corrections for hot wires. Meas. Sci. Technol. 21 (10), 105404.CrossRefGoogle Scholar
Jiménez, J. M.2007 High Reynolds number flows about bodies of revolution with application to submarines and torpedoes. PhD thesis, Princeton University.Google Scholar
Jiménez, J. M., Hultmark, M. & Smits, A. J. 2010a The intermediate wake of a body of revolution at high Reynolds number. J. Fluid Mech. 659, 516–539.CrossRefGoogle Scholar
Jiménez, J. M., Reynolds, R. T. & Smits, A. J. 2010b The effects of fins on the intermediate wake of a submarine model. Trans. ASME J. Fluids Engng 132, 031102.CrossRefGoogle Scholar
Johansson, P. B. V. & George, W. K. 2006 The far downstream evolution of the high Reynolds number axisymmetric wake behind a disk. Part I. Single-point statistics. J. Fluid Mech. 555, 363–385.CrossRefGoogle Scholar
Karlsson, A. & Fureby, C. 2009 LES of the flow past a 6:1 prolate spheroid. In 47th AIAA Aerospace Sciences Meeting, Washington, DC, AIAA.Google Scholar
Keener, E. R. & Chapman, G. T. 1977 Similarity in vortex asymmetries over slender bodies and wings. AIAA J. 15 (9), 1370–1372.CrossRefGoogle Scholar
Lloyd, A. R. J. M. & Campbell, I. M. C. 1986 Experiments to investigate the vortices shed from a submarine-like body of revolution. In Proceedings of the 59th Meeting of AGARD Fluid Dynamics Panel Symposium. Monterey, CA, AGARD; 33-1–33-22.Google Scholar
Nelson, R. C. & Pelletier, A. 2003 The unsteady aerodynamics of slender wings and aircraft undergoing large amplitude maneuvers. Prog. Aerosp. Sci. 39, 185–248.CrossRefGoogle Scholar
Perry, A. E. & Lim, T. T. 1978 Coherent structures in coflowing jets and wakes. J. Fluid Mech. 88, 451–463.CrossRefGoogle Scholar
Vatsa, V. N., Thomas, J. L. & Wedan, B. W. 1989 Navier–Stokes computations of a prolate spheroid at angle of attack. J. Aircraft 26 (11), 986–993.CrossRefGoogle Scholar
Werlé, H. 1962 Separation on axisymmetrical bodies at low speed. Rech. Aéronaut. 90, 3–14.Google Scholar