Article contents
Assessment of inner–outer interactions in the urban boundary layer using a predictive model
Published online by Cambridge University Press: 18 July 2019
Abstract
Urban-type rough-wall boundary layers developing over staggered cube arrays with plan area packing density, 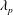 $\unicode[STIX]{x1D706}_{p}$, of 6.25 %, 25 % or 44.4 % have been studied at two Reynolds numbers within a wind tunnel using hot-wire anemometry (HWA). A fixed HWA probe is used to capture the outer-layer flow while a second moving probe is used to capture the inner-layer flow at 13 wall-normal positions between
$\unicode[STIX]{x1D706}_{p}$, of 6.25 %, 25 % or 44.4 % have been studied at two Reynolds numbers within a wind tunnel using hot-wire anemometry (HWA). A fixed HWA probe is used to capture the outer-layer flow while a second moving probe is used to capture the inner-layer flow at 13 wall-normal positions between 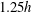 $1.25h$ and
$1.25h$ and 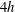 $4h$ where
$4h$ where 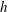 $h$ is the height of the roughness elements. The synchronized two-point HWA measurements are used to extract the near-canopy large-scale signal using spectral linear stochastic estimation and a predictive model is calibrated in each of the six measurement configurations. Analysis of the predictive model coefficients demonstrates that the canopy geometry has a significant influence on both the superposition and amplitude modulation. The universal signal, the signal that exists in the absence of any large-scale influence, is also modified as a result of local canopy geometry suggesting that although the nonlinear interactions within urban-type rough-wall boundary layers can be modelled using the predictive model as proposed by Mathis et al. (J. Fluid Mech., vol. 681, 2011, pp. 537–566), the model must be however calibrated for each type of canopy flow regime. The Reynolds number does not significantly affect any of the model coefficients, at least over the limited range of Reynolds numbers studied here. Finally, the predictive model is validated using a prediction of the near-canopy signal at a higher Reynolds number and a prediction using reference signals measured in different canopy geometries to run the model. Statistics up to the fourth order and spectra are accurately reproduced demonstrating the capability of the predictive model in an urban-type rough-wall boundary layer.
$h$ is the height of the roughness elements. The synchronized two-point HWA measurements are used to extract the near-canopy large-scale signal using spectral linear stochastic estimation and a predictive model is calibrated in each of the six measurement configurations. Analysis of the predictive model coefficients demonstrates that the canopy geometry has a significant influence on both the superposition and amplitude modulation. The universal signal, the signal that exists in the absence of any large-scale influence, is also modified as a result of local canopy geometry suggesting that although the nonlinear interactions within urban-type rough-wall boundary layers can be modelled using the predictive model as proposed by Mathis et al. (J. Fluid Mech., vol. 681, 2011, pp. 537–566), the model must be however calibrated for each type of canopy flow regime. The Reynolds number does not significantly affect any of the model coefficients, at least over the limited range of Reynolds numbers studied here. Finally, the predictive model is validated using a prediction of the near-canopy signal at a higher Reynolds number and a prediction using reference signals measured in different canopy geometries to run the model. Statistics up to the fourth order and spectra are accurately reproduced demonstrating the capability of the predictive model in an urban-type rough-wall boundary layer.
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 12
- Cited by


