Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-26T16:34:01.417Z Has data issue: false hasContentIssue false
  • English
  • Français

Ascending–descending and direct–inverse cascades of Reynolds stresses in turbulent Couette flow

Published online by Cambridge University Press:  08 November 2021

Alessandro Chiarini Open the ORCID record for Alessandro Chiarini [Opens in a new window] ,
Mariadebora Mauriello Open the ORCID record for Mariadebora Mauriello [Opens in a new window] ,
Davide Gatti Open the ORCID record for Davide Gatti [Opens in a new window]  and
Maurizio Quadrio Open the ORCID record for Maurizio Quadrio [Opens in a new window]
Alessandro Chiarini
Affiliation:
Dipartimento di Scienze e Tecnologie Aerospaziali, Politecnico di Milano, via La Masa 34, 20156Milano, Italy
Mariadebora Mauriello
Affiliation:
Dipartimento di Scienze e Tecnologie Aerospaziali, Politecnico di Milano, via La Masa 34, 20156Milano, Italy
Davide Gatti
Affiliation:
Institute for Fluid Mechanics, Karlsruhe Institute of Technology, Kaiserstr. 10, 76131Karlsruhe, Germany
Maurizio Quadrio*
Affiliation:
Dipartimento di Scienze e Tecnologie Aerospaziali, Politecnico di Milano, via La Masa 34, 20156Milano, Italy
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

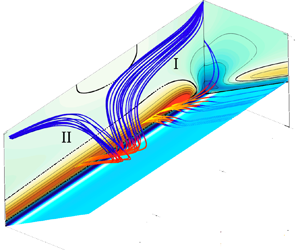
The interaction between small- and large-scale structures and the coexisting bottom-up and top-down processes are studied in a turbulent plane Couette flow, where space-filling longitudinal rolls appear at relatively low values of the Reynolds number $Re$. A direct numerical simulation database at $Re_\tau =101$ is built to replicate the highest $Re$ considered in recent experimental work by Kawata & Alfredsson (Phys. Rev. Lett., vol. 120, 2018, 244501). Our study is based on the exact budget equations for the second-order structure function tensor $\left \langle {\delta u_i \delta u_j} \right \rangle$, i.e. the anisotropic generalized Kolmogorov equations (AGKE). The AGKE study production, redistribution, transport and dissipation of every Reynolds stress tensor component, considering simultaneously the physical space and the space of scales, and properly define the concept of scale in the inhomogeneous wall-normal direction. We show how the large-scale energy-containing motions are involved in the production and redistribution of the turbulent fluctuations. Both bottom-up and top-down interactions occur, and the same is true for direct and inverse cascading. The wall-parallel components $\left \langle {\delta u \delta u} \right \rangle$ and $\left \langle {\delta w \delta w} \right \rangle$ show that both small and large near-wall scales feed the large scales away from the wall. The wall-normal component $\left \langle {\delta v \delta v} \right \rangle$ is different, and shows a dominant top-down dynamics, being produced via pressure-strain redistribution away from the wall and transferred towards near-wall larger scales via an inverse cascade. The off-diagonal component shows a top-down interaction, with both direct and inverse cascades, albeit the latter takes place within a limited range of scales.

JFM classification

Turbulent Flows: Shear layer turbulence
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 930 , 10 January 2022 , A9
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

Present address: Aix-Marseille Univ., CNRS, IUSTI UMR 7343, 13013 Marseille, France.

References

REFERENCES

Andreolli, A., Quadrio, M. & Gatti, D. 2021 Global energy budgets in turbulent Couette and Poiseuille flows. J. Fluid Mech. 924, A25.CrossRefGoogle Scholar
Cheng, C., Li, W., Lozano-Durán, A. & Liu, H. 2020 On the structure of streamwise wall-shear stress fluctuations in turbulent channel flows. J. Fluid Mech. 903, A29.CrossRefGoogle Scholar
Cho, M., Hwang, Y. & Choi, H. 2018 Scale interactions and spectral energy transfer in turbulent channel flow. J. Fluid Mech. 854, 474–504.CrossRefGoogle Scholar
Cimarelli, A., De Angelis, E. & Casciola, C.M. 2013 Paths of energy in turbulent channel flows. J. Fluid Mech. 715, 436–451.CrossRefGoogle Scholar
Cimarelli, A., De Angelis, E., Jimenez, J. & Casciola, C.M. 2016 Cascades and wall-normal fluxes in turbulent channel flows. J. Fluid Mech. 796, 417–436.CrossRefGoogle Scholar
Cimarelli, A., Mollicone, J.-P., van Reeuwijk, M. & De Angelis, E. 2021 Spatially evolving cascades in temporal planar jets. J. Fluid Mech. 910, A19.CrossRefGoogle Scholar
Flores, O., Jiménez, J. & Del Álamo, J.C. 2007 Vorticity organization in the outer layer of turbulent channels with disturbed walls. J. Fluid Mech. 591, 145–154.CrossRefGoogle Scholar
Gatti, D., Chiarini, A., Cimarelli, A. & Quadrio, M. 2020 Structure function tensor equations in inhomogeneous turbulence. J. Fluid Mech. 898, A5.CrossRefGoogle Scholar
Gatti, D., Remigi, A., Chiarini, A., Cimarelli, A. & Quadrio, M. 2019 An efficient numerical method for the generalized Kolmogorov equation. J. Turbul. 20 (8), 457–480.CrossRefGoogle Scholar
Guala, M., Hommema, S.E. & Adrian, R.J. 2006 Large-scale and very-large-scale motions in turbulent pipe flow. J. Fluid Mech. 554, 521–542.CrossRefGoogle Scholar
Hill, R.J. 2001 Equations relating structure functions of all orders. J. Fluid Mech. 434, 379–388.CrossRefGoogle Scholar
Hwang, Y. & Cossu, C. 2010 Self-sustained process at large scales in turbulent channel flow. Phys. Rev. Lett. 105 (4), 044505.CrossRefGoogle ScholarPubMed
Illingworth, S.J. 2020 Streamwise-constant large-scale structures in Couette and Poiseuille flows. J. Fluid Mech. 889, A13.CrossRefGoogle Scholar
Jiménez, J. & Pinelli, A. 1999 The autonomous cycle of near-wall turbulence. J. Fluid Mech. 389, 335–359.CrossRefGoogle Scholar
Kawata, T. & Alfredsson, P.H. 2018 Inverse interscale transport of the Reynolds shear stress in plane Couette turbulence. Phys. Rev. Lett. 120 (24), 244501.CrossRefGoogle ScholarPubMed
Kawata, T. & Alfredsson, P.H. 2019 Scale interactions in turbulent rotating planar Couette flow: insight through the Reynolds stress transport. J. Fluid Mech. 879, 255–295.CrossRefGoogle Scholar
Kawata, T. & Tsukahara, T. 2021 Scale interactions in turbulent plane Couette flows in minimal domains. J. Fluid Mech. 911, A55.CrossRefGoogle Scholar
Lee, M. & Moser, R.D. 2018 Extreme-scale motions in turbulent plane Couette flows. J. Fluid Mech. 842, 128–145.CrossRefGoogle Scholar
Lee, M. & Moser, R.D. 2019 Spectral analysis of the budget equation in turbulent channel flows at high Re. J. Fluid Mech. 860, 886–938.CrossRefGoogle Scholar
Luchini, P. & Quadrio, M. 2006 A low-cost parallel implementation of direct numerical simulation of wall turbulence. J. Comput. Phys. 211 (2), 551–571.CrossRefGoogle Scholar
Mansour, N., Kim, J. & Moin, P. 1988 Reynolds-stress and dissipation-rate budgets in a turbulent channel flow. J. Fluid Mech. 194, 15–44.CrossRefGoogle Scholar
Mizuno, Y. 2016 Spectra of energy transport in turbulent channel flows for moderate Reynolds numbers. J. Fluid Mech. 805, 171–187.CrossRefGoogle Scholar
Mollicone, J.-P., Battista, F., Gualtieri, P. & Casciola, C.M. 2018 Turbulence dynamics in separated flows: the generalised Kolmogorov equation for inhomogeneous anisotropic conditions. J. Fluid Mech. 841, 1012–1039.CrossRefGoogle Scholar
Orlandi, P., Bernardini, M. & Pirozzoli, S. 2015 Poiseuille and Couette flows in the transitional and fully turbulent regime. J. Fluid Mech. 770, 424–441.CrossRefGoogle Scholar
Pope, S.B. 2000 Turbulent Flows. Cambridge University Press.CrossRefGoogle Scholar
Portela, F.A., Papadakis, G. & Vassilicos, J.C. 2017 The turbulence cascade in the near wake of a square prism. J. Fluid Mech. 825, 315–352.CrossRefGoogle Scholar
Smits, A.J., McKeon, B.J. & Marusic, I. 2011 High-Reynolds number wall turbulence. Annu. Rev. Fluid Mech. 43 (1), 353–375.CrossRefGoogle Scholar
Togni, R., Cimarelli, A. & De Angelis, E. 2015 Physical and scale-by-scale analysis of Rayleigh–Bénard convection. J. Fluid Mech. 782, 380–404.CrossRefGoogle Scholar
Toh, S. & Itano, T. 2005 Interaction between a large-scale structure and near-wall structures in channel flow. J. Fluid Mech. 524, 249–262.CrossRefGoogle Scholar
Tsukahara, T., Kawamura, H. & Shingai, K. 2006 DNS of turbulent Couette flow with emphasis on the large-scale structure in the core region. J. Turbul. 7, N19.CrossRefGoogle Scholar